相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、设l,m,n是不同的直线,m,n在平面内,则“且”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
2、的一个充分不必要条件是( )A、 B、 C、 D、
-
3、在校运动会上,有甲、乙、丙三位同学参加羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、丙首先比赛,乙轮空.设每场比赛双方获胜的概率都为.(1)、求丙连胜四场的概率;(2)、求需要进行第五场比赛的概率;(3)、甲、乙、丙三人中谁最终获胜的概率最大?请说明理由.
-
4、如图,在直三棱柱中, , , 点M,N分别为和的中点.
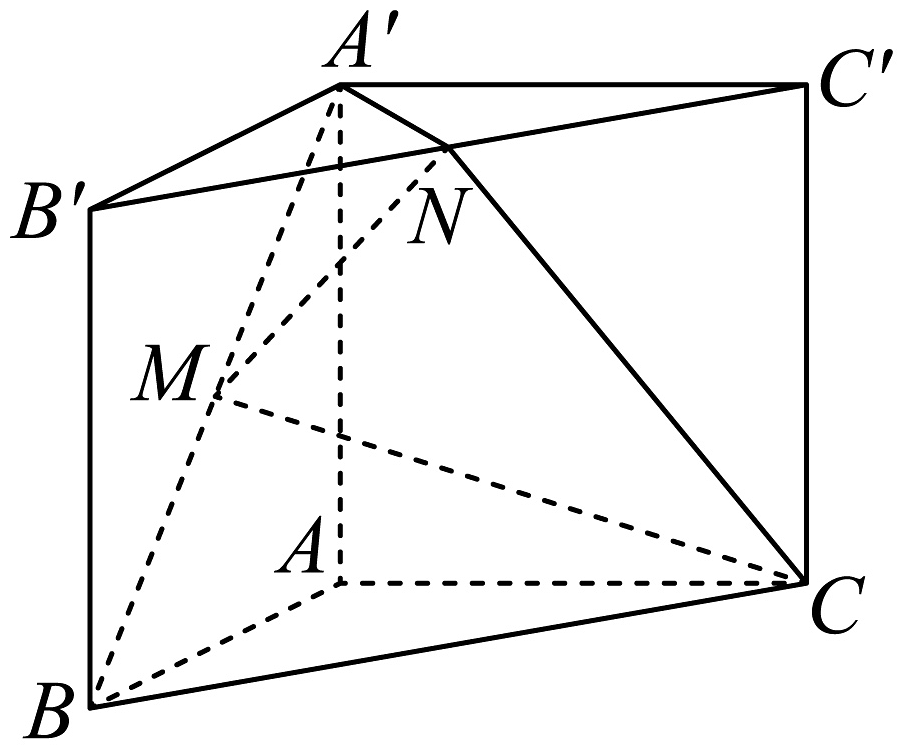 (1)、证明:平面;(2)、求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值. -
5、如图,在平行六面体中,以顶点为端点的三条棱长都是1,且它们彼此的夹角都是 , 为与的交点.若 , , ,
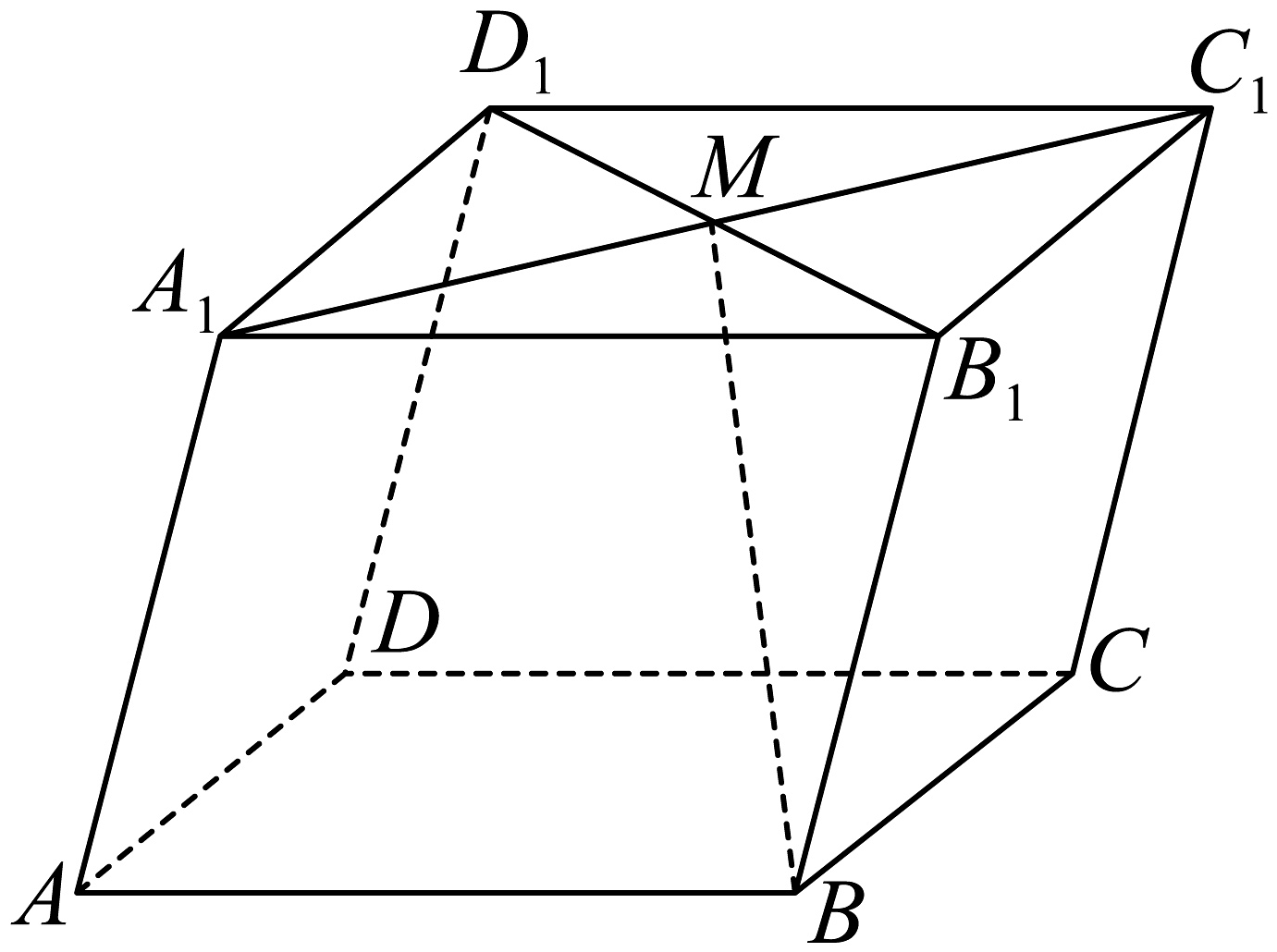
(1)用表示;
(2)求对角线的长;
(3)求
-
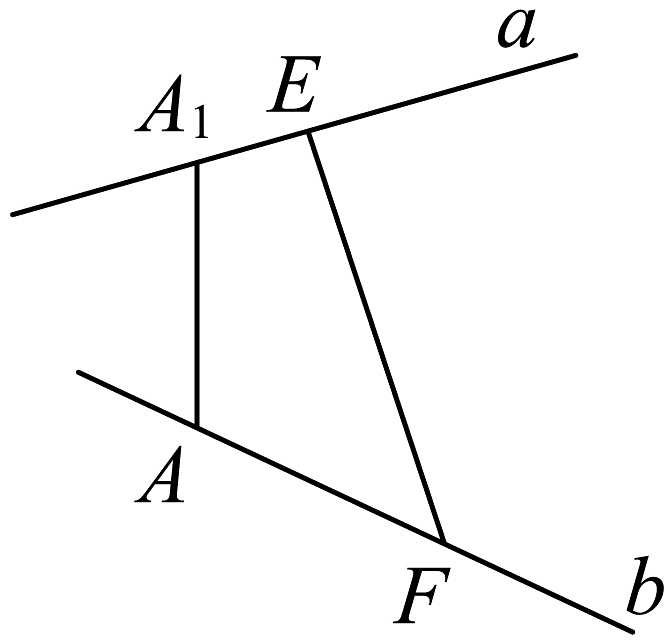
6、如图,两条异面直线所成的角为 , 在直线上分别取点和点 , 使.已知 , 则.
-
7、某专业技术的考试共两个单项考试,考生应依次参加两个单项考试,前一项考试合格后才能报名参加后一项考试,考试不合格则需另行交费预约再次补考.据调查,这两项考试的合格率依次为 , , 且各项考试是否通过互不影响,则一位考生通过这项专业技术考试至多需要补考一次的概率为.
-
8、已知向量 , , 若与垂直,则.
-
9、如图,在三棱柱中,侧面与是边长为2的正方形,平面平面 , 分别在和上,且 , 则( )
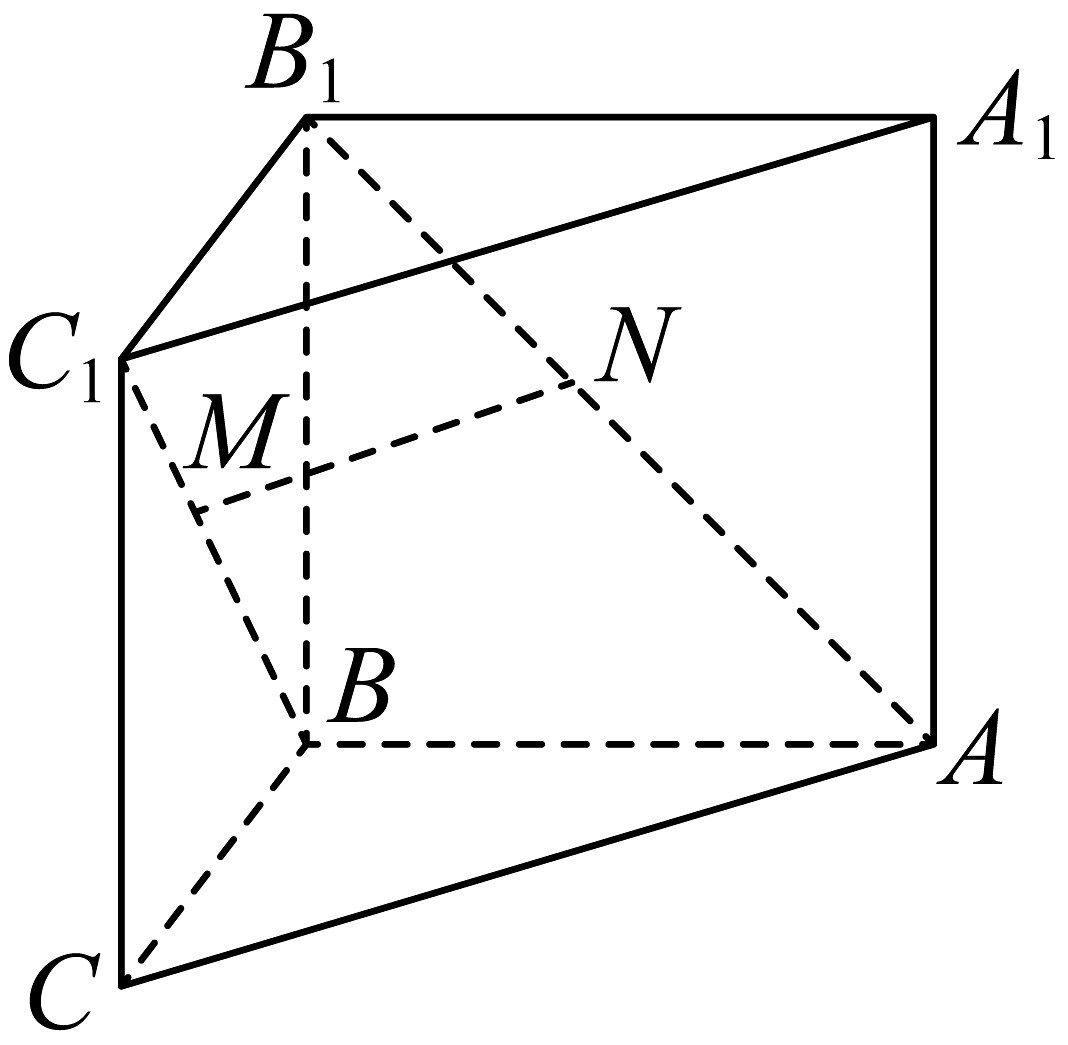 A、直线平面 B、当时,线段的长最小 C、当时,直线与平面所成角的正切值为 D、当时,平面与平面夹角的余弦值为
A、直线平面 B、当时,线段的长最小 C、当时,直线与平面所成角的正切值为 D、当时,平面与平面夹角的余弦值为 -
10、下列四个命题中,正确命题的有( )A、已知向量 , , 共面,则实数t的值为0 B、若向量 , 且与的夹角为钝角,则实数m的取值范围为 C、已知直线l的方向向量为 , 点在l上,则点到l的距离为 D、若两个不同平面 , 的法向量分别是 , , 且 , , 则
-
11、已知正方体的棱长为4,点E是棱的中点,动点P在正方形内(包括边界)运动,且平面 , 则长度的取值范围为( )A、 B、 C、 D、
-
12、如图,点P为矩形所在平面外一点,平面 , Q为的中点, , , , 则点P到平面的距离为( )
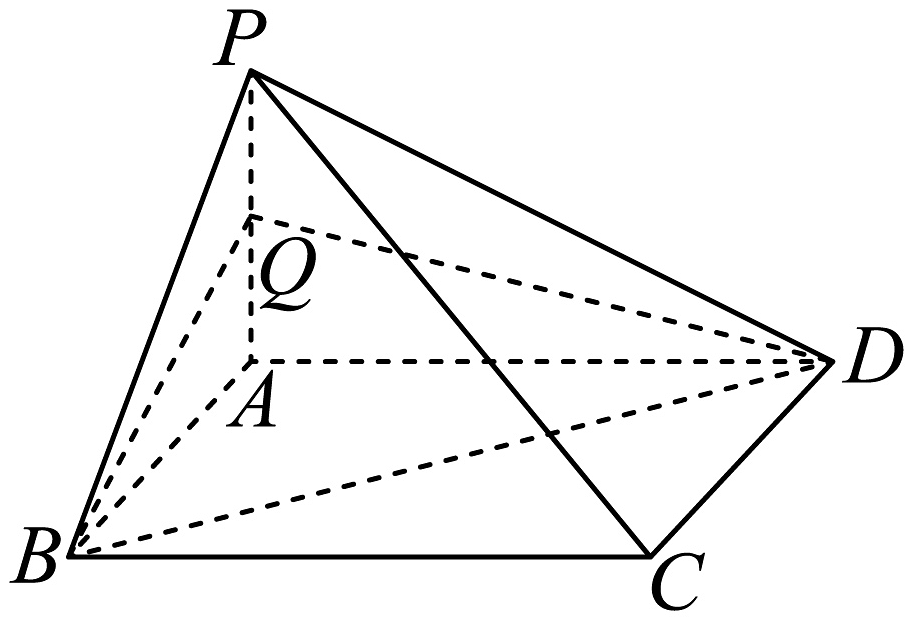 A、 B、 C、 D、
A、 B、 C、 D、 -
13、已知点D在确定的平面内,O是平面ABC外任意一点,满足 , 且 , , 则的最小值为( )A、 B、 C、 D、
-
14、同时抛掷一红一绿两枚质地均匀的骰子,用x表示红色骰子的点数,y表示绿色骰子的点数,设事件“”,事件“不能被2整除”,则( )A、 B、 C、 D、
-
15、已知某运动员每次投篮命中的概率都为 , 现采用随机模拟的方式估计该运动员三次投篮恰有两次命中的概率:先由计算机产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以三个随机数为一组,代表三次投篮结果,经随机模拟产生了如下12组随机数:137 960 197 925 271 815 952 683 123 436 730 257,据此估计,该运动员三次投篮恰有两次命中的概率为( )A、 B、 C、 D、
-
16、已知点 , 点C与点A关于平面Oxy对称,点B与点A关于z轴对称,则线段BC的长为( )A、 B、4 C、 D、
-
17、已知非零向量 , 则“”是“”的( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、非必要非充分条件
-
18、中国古代数学著作主要有《周髀算经》,《九章算术》,《海岛算经》,《四元玉鉴》,《张邱建算经》,若从上述5部书籍中任意抽取2部,则抽到《九章算术》的概率为( )A、 B、 C、 D、
-
19、已知 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
20、若平面与平面平行, , 则直线的位置关系为 .