相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知整数 , 数列是递增的整数数列,即且 . 数列满足 , . 若对于 , 恒有等于同一个常数 , 则称数列为的“左型间隔数列”;若对于 , 恒有等于同一个常数 , 则称数列为的“右型间隔数列”;若对于 , 恒有或者 , 则称数列为的“左右型间隔数列”.(1)、写出数列的所有递增的“左右1型间隔数列”;(2)、已知数列满足 , 数列是的“左型间隔数列”,数列是的“右型间隔数列”,若 , 且有 , 求的值;(3)、数列是递增的整数数列,且 , . 若存在的一个递增的“右4型间隔数列”,使得对于任意的 , 都有 , 求的关于的最小值(即关于的最小值函数).
-
2、数学老师在黑板上写上一个实数 , 然后老师抛掷一枚质地均匀的硬币,如果正面向上,就将黑板上的数乘以再加上3得到 , 并将擦掉后将写在黑板上;如果反面向上,就将黑板上的数除以再减去3得到 , 也将擦掉后将写在黑板上.然后老师再抛掷一次硬币重复刚才的操作得到黑板上的数为 . 现已知的概率为0.5,则实数的取值范围是 .
-
3、若对任意 , 有 , 则函数在上的最大值与最小值的和 .
-
4、《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如, , 求证: . 证明:原式 .
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式( , ),当且仅当时等号成立,它是解决最值问题的有力工具.例如:在的条件下,当为何值时,有最小值,最小值是多少?
解: , , , 即 , , 当且仅当 , 即时,有最小值,最小值为2.请根据以上阅读材料解答下列问题:
(1)、已知 , 求的值.(2)、若 , 解关于的方程 .(3)、若正数 , 满足 , 求的最小值. -
5、已知 , 则( )A、 B、 C、 D、
-
6、已知函数 .
(1)当时,求曲线在点处的切线与两坐标轴围成的三角形的面积;
(2)若不等式恒成立,求a的取值范围.
-
7、已知数列满足.
(1)证明是等比数列,并求的通项公式;
(2)证明: .
-
8、等比数列中, .
(1)求的通项公式;
(2)记为的前项和.若 , 求 .
-
9、等差数列中,设数列满足 ,(1)、求数列通项公式;(2)、设 , 求数列的前8项和.
-
10、为等比数列的前三项,则的可能值为( )A、4 B、5 C、 D、
-
11、设集合A={1,2,3},集合B={﹣2,2},则A∩B=( )A、∅ B、{2} C、{﹣2,2} D、{﹣2,1,2,3}
-
12、如图,已知正方体 , 点在直线上,为线段的中点,则下列命题中假命题为( )
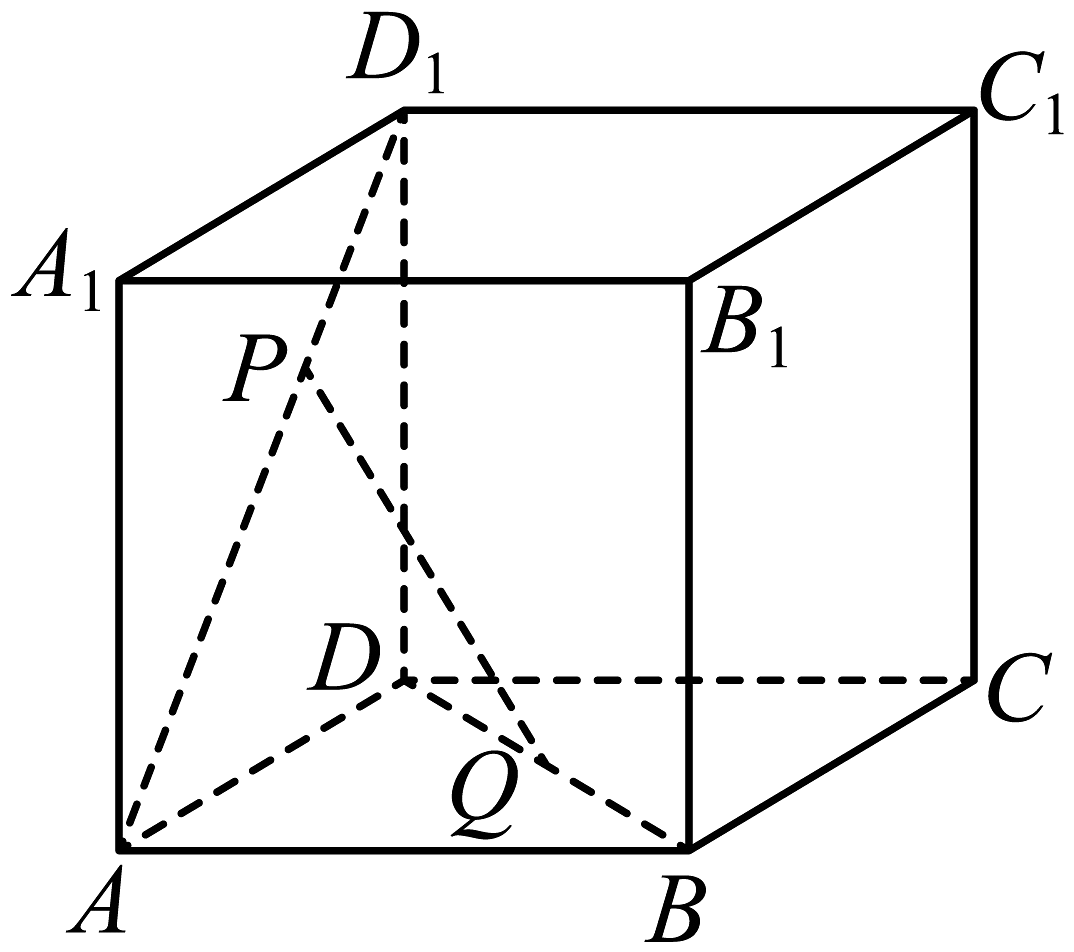 A、存在点 , 使得 B、存在点 , 使得 C、直线始终与直线异面 D、直线始终与直线异面
A、存在点 , 使得 B、存在点 , 使得 C、直线始终与直线异面 D、直线始终与直线异面 -
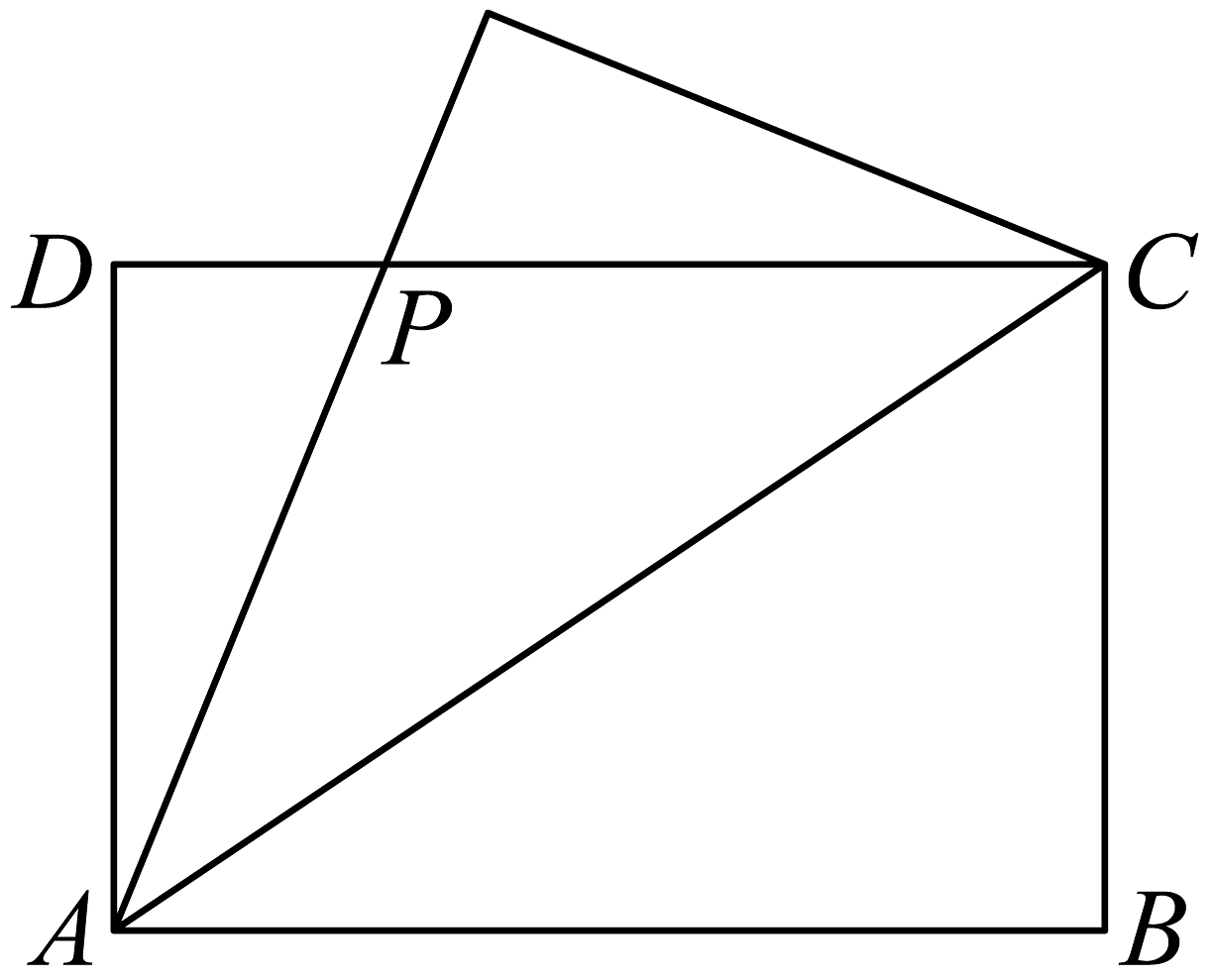
13、在学习完基本不等式与一元二次方程这一章节后,某校高一数学老师带领全班同学在数学课堂上做了一个有趣的实验,该实验的目的主要是体现不等式在实际生活中的应用老师要求同学们准备了一张周长为的矩形纸片(其中),将沿向折叠,折过去后交于点.如果在保持矩形周长不变且折过去后交于点的情况下,适度改变的长度,问:的面积是否存在最大值?若存在,求出其最大值;若不存在,说明理由.
-
14、已知二次函数满足 , 且.(1)、求的解析式;(2)、集合 , 若 , 求实数的取值范围.
-
15、已知函数 , 且.(1)、求;(2)、判断函数在上的单调性,并用定义法证明;(3)、求函数在区间上的最大值和最小值.
-
16、已知集合 , , .(1)、求 , , ;(2)、若 , 求实数的取值范围.
-
17、已知函数 , 满足对任意的实数且 , 都有 , 则实数a的取值范围是.
-
18、函数的单调递增区间为 .
-
19、高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设 , 用表示不超过x的最大整数,则称为高斯函数,如.设函数 , 则下列说法错误的是( )A、的图象关于轴对称 B、的最大值为1,没有最小值 C、 D、在上是增函数
-
20、下列四个结论中,正确的结论是( )A、与表示同一个函数. B、“”的充分不必要条件是“”. C、已知 , 则的取值范围的取值范围是 . D、函数的值域为 .