版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、设各项非零的数列 $\{a_{n}\}$ 的前n项和记为 $S_{n}$ ，记 $T_{n} = S_{1} \cdot S_{2} \cdot S_{3} \cdot \cdot \cdot \cdot \cdot S_{n}$ ，且满足 $2 S_{n} T_{n} - S_{n} - 2 T_{n} = 0$ ，

(1)、求 $T_{1}$ ， $T_{2}$ 的值，并求数列 $\{T_{n}\}$ 的通项公式；

(2)、设 $c_{n} = a_{n} + \frac{{(- 1)}^{n}}{n a_{n}}$ ，求数列 $\{c_{n}\}$ 的前n项和 $K_{n}$ ．

查看解析
2、随着5G网络信号的不断完善，5G手机已经成为手机销售市场的明星．某地区手机专卖商场对已售出的1000部5G手机的价格数据进行分析得到如图所示的频率分布直方图：

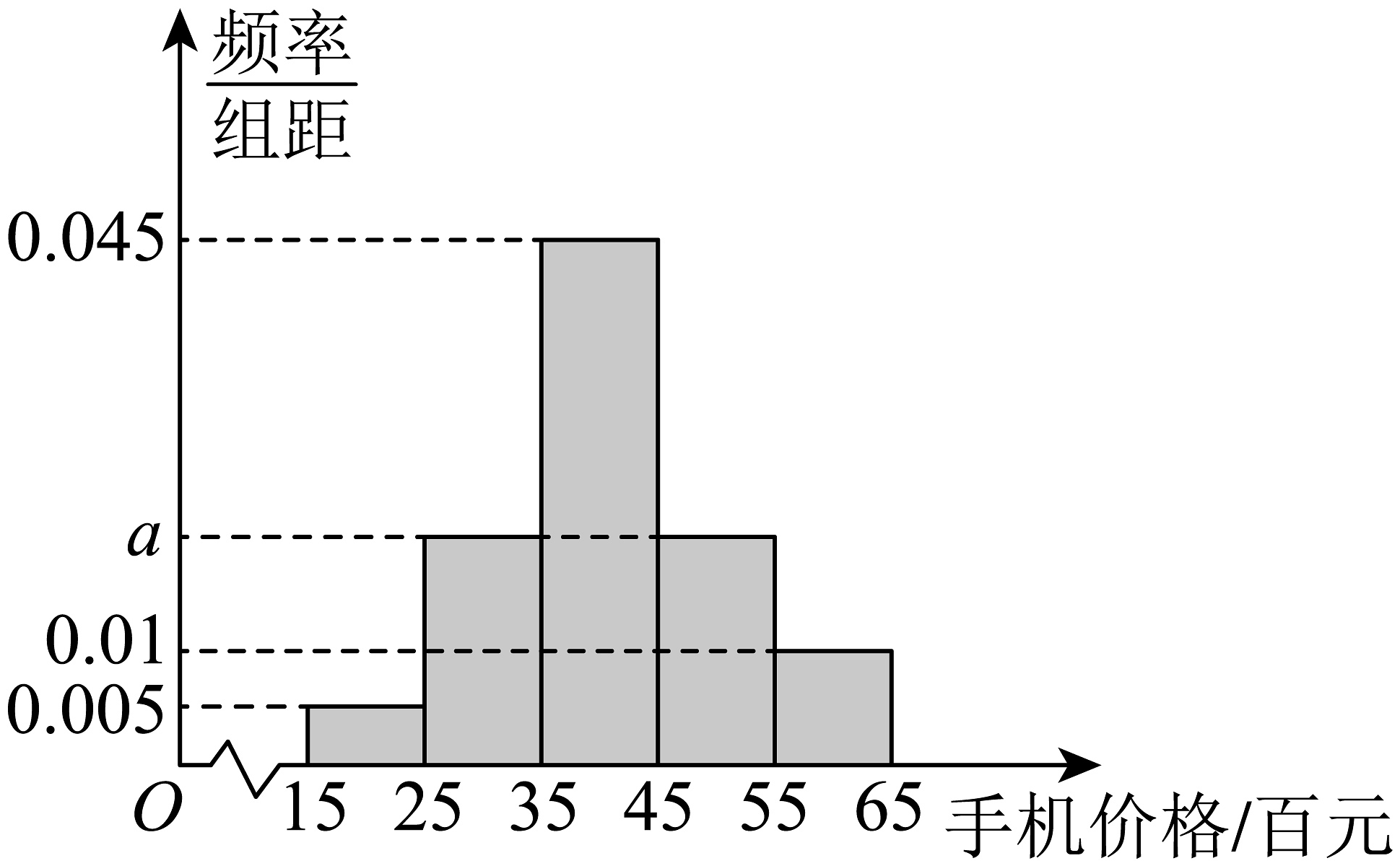(1)、求5G手机的价格75%分位数；

(2)、某夫妻两人到该商场准备购买价位在4500~6500的手机各一部，商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部，假定选择每部手机是等可能的，设这两人购买同一价位区间的手机的数量为X，求 $E (X)$

查看解析
3、若曲线 $y = ln (x + 1) + x$ 在原点处的切线也是曲线 $y = e^{x} - 2 + a$ 的切线，则 $a =$ ．

查看解析
4、设函数 $f (x) = 2 x^{3} - 3 a x^{2} + 1$ ，则（）

A、存在a，b，使得 $x = b$ 为曲线 $y = f (x)$ 的对称轴 B、存在a，使得点 $(1, f (1))$ 为曲线 $y = f (x)$ 的对称中心 C、当 $a < 0$ 时， $x = a$ 是 $f (x)$ 的极大值点 D、当 $a > 1$ 时， $f (x)$ 有三个零点

查看解析
5、豆瓣评分是将用户评价的一到五星转化为0-10的分值（一星2分，二星4分，三星6分，以此类推），以得分总和除以评分的用户人数所得的数字，国庆爱国影片《长津湖》豆瓣得分是7.4分，截止至2021年10月24日，共计有437181人参与评分，豆瓣评分表如下．根据猫眼实时数据，该片的票房为53.1亿元，按照平均票价50元来计算，大约有1亿人次观看了此片，假如参与评分观众中有97.6%的评价不低于二星，则下列说法正确的是（）

A、m的值是32% B、随机抽取100名观众，则一定有24人评价五星 C、若以频率当作概率，记事件A为“评价是一星”，事件B为“评价不高于二星”，则 $P (B | A) = \frac{8}{37}$ D、若从已作评价的观众中随机抽出3人，则事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件

查看解析
6、已知向量 $\vec{m} = (cos α, sin (π + α))$ ， $\vec{n} = (sin (\frac{π}{2} + β), sin β)$ 则（）

A、 $\vec{m} \cdot \vec{n} = cos (α + β)$ B、 ${\vec{m}}^{2} + {\vec{n}}^{2} = 2$ C、若 $\vec{m} ∥ \vec{n}$ ，则 $α + β = 2 k π (k \in Z)$ D、 $|\vec{m} + \vec{n}| \leq 2$

查看解析
7、设函数 $f (x) = {\begin{matrix} | \ln x |, x > 0 \\ e^{x} (x + 1), x \leq 0 \end{matrix}$ ，若方程 ${[f (x)]}^{2} - a f (x) + \frac{1}{16} = 0$ 有六个不等的实数根，则实数a可取的值可能是（）

A、 $\frac{2}{3}$ B、 $\frac{2}{3}$ 或1 C、1 D、 $\frac{2}{3}$ 或2

查看解析
8、已知椭圆 $E$ ： $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ 的左右顶点分别为 $A_{1}$ ， $A_{2}$ ，圆 $O_{1}$ 的方程为 ${(x + 1)}^{2} + {(y - \frac{\sqrt{3}}{2})}^{2} = \frac{1}{4}$ ，动点 $P$ 在曲线 $E$ 上运动，动点 $Q$ 在圆 $O_{1}$ 上运动，若 $△ A_{1} A_{2} P$ 的面积为 $4 \sqrt{3}$ ，记 $|P Q|$ 的最大值和最小值分别为 $m$ 和 $n$ ，则 $m + n$ 的值为（）

A、 $\sqrt{7}$ B、 $2 \sqrt{7}$ C、 $3 \sqrt{7}$ D、 $4 \sqrt{7}$

查看解析
9、已知 ${(a x + \frac{b}{\sqrt{x}})}^{6}$ 的展开式中 $x^{\frac{3}{2}}$ 项的系数为160，则当 $a > 0$ ， $b > 0$ 时， $a + b$ 的最小值为（）

A、4 B、 $2 \sqrt{2}$ C、2 D、 $\sqrt{2}$

查看解析
10、风车又称“风谷车”，相传是春秋时期鲁国人鲁班发明，由风车肚、摇手、漏斗、出风口等部件组成．风车的工作原理是摇动叶片形成恰当的风力，风吹谷子将谷壳与谷粒分离．已知某风车将谷壳和谷粒分离后，谷壳和谷粒体积的比例大概为1：5，顶部梯形状的漏斗（谷子的入料仓，也称“盛斗”）可看作是正四棱台，如图2所示，该几何体上、下底面边长分别为 $30cm$ ， $18cm$ ，若使用该风车将漏斗装满后，分离出的谷粒有 ${6860cm}^{3}$ ，则漏斗的高为（）

A、 $\frac{8575}{882} cm$ B、 $\frac{8575}{588} cm$ C、 $14cm$ D、 $42cm$

查看解析
11、已知 $a = \sqrt[4]{π}$ ， $b = \log_{\frac{1}{4}} (l nπ)$ ， $c = {(\frac{1}{4})}^{1.7}$ 则a，b，c的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < a < b$ D、 $b < c < a$

查看解析
12、若 $\frac{z}{z - 1} = 1 + i$ ，则复数 $z$ 的模为（）

A、 $1 - i$ B、 $1 + i$ C、 $\sqrt{2}$ D、 $2$

查看解析
13、若存在常数 $t$ ，使得数列 $\{a_{n}\}$ 满足 $a_{n + 1} - a_{1} a_{2} a_{3} \dots a_{n} = t (n \geq 1, n \in N)$ ，则称数列 $\{a_{n}\}$ 为“ $H (t)$ 数列”．

(1)、判断数列：1，3，5，10，152是否为“ $H (2)$ 数列”，并说明理由；

(2)、若数列 $\{a_{n}\}$ 是首项为2的“ $H (t)$ 数列”，数列 $\{b_{n}\}$ 是等比数列，且 $\{a_{n}\}$ 与 $\{b_{n}\}$ 满足 $\sum_{i = 1}^{n} a_{i}^{2} = a_{1} a_{2} a_{3} \dots a_{n} + \log_{2} b_{n}$ ，求 $t$ 的值和数列 $\{b_{n}\}$ 的通项公式；

(3)、若数列 $\{a_{n}\}$ 是“ $H (t)$ 数列”， $S_{n}$ 为数列 $\{a_{n}\}$ 的前 $n$ 项和， $a_{1} > 1$ ， $t > 0$ ，证明： $t > S_{n + 1} - S_{n} - e^{S_{n} - n}$ ．

查看解析
14、已知复数z满足 $z (1 - i) = {|1 + i|}^{2}$ ，则 $z =$ （）

A、 $1 - i$ B、 $1 + i$ C、 $- 1 - i$ D、 $- 1 + i$

查看解析
15、定义运算： $|\begin{matrix} m & n \\ p & q \end{matrix}| = m q - n p$ ，已知函数 $f (x) = |\begin{matrix} \ln x & x - 1 \\ 1 & a \end{matrix}|$ ， $g (x) = \frac{1}{x} - 1$ ．

(1)、若函数 $f (x)$ 的最大值为0，求实数a的值；

(2)、若函数 $h (x) = f (x) + g (x)$ 存在两个极值点 $x_{1}$ ， $x_{2}$ ，证明： $\frac{h (x_{1}) - h (x_{2})}{x_{1} - x_{2}} - a + 2 < 0$ ；

(3)、证明： $(1 + \frac{1}{2^{2}}) (1 + \frac{1}{3^{2}}) (1 + \frac{1}{4^{2}}) ... (1 + \frac{1}{n^{2}}) < e$ ．

查看解析
16、已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点别为 $F_{1}$ ， $F_{2}$ ，离心率为 $\frac{\sqrt{2}}{2}$ ，过点 $F_{1}$ 的动直线l交E于A，B两点，点A在x轴上方，且l不与x轴垂直， $△ A B F_{2}$ 的周长为 $4 \sqrt{2}$ ，直线 $A F_{2}$ 与E交于另一点C，直线 $B F_{2}$ 与E交于另一点D，点P为椭圆E的下顶点，如图．

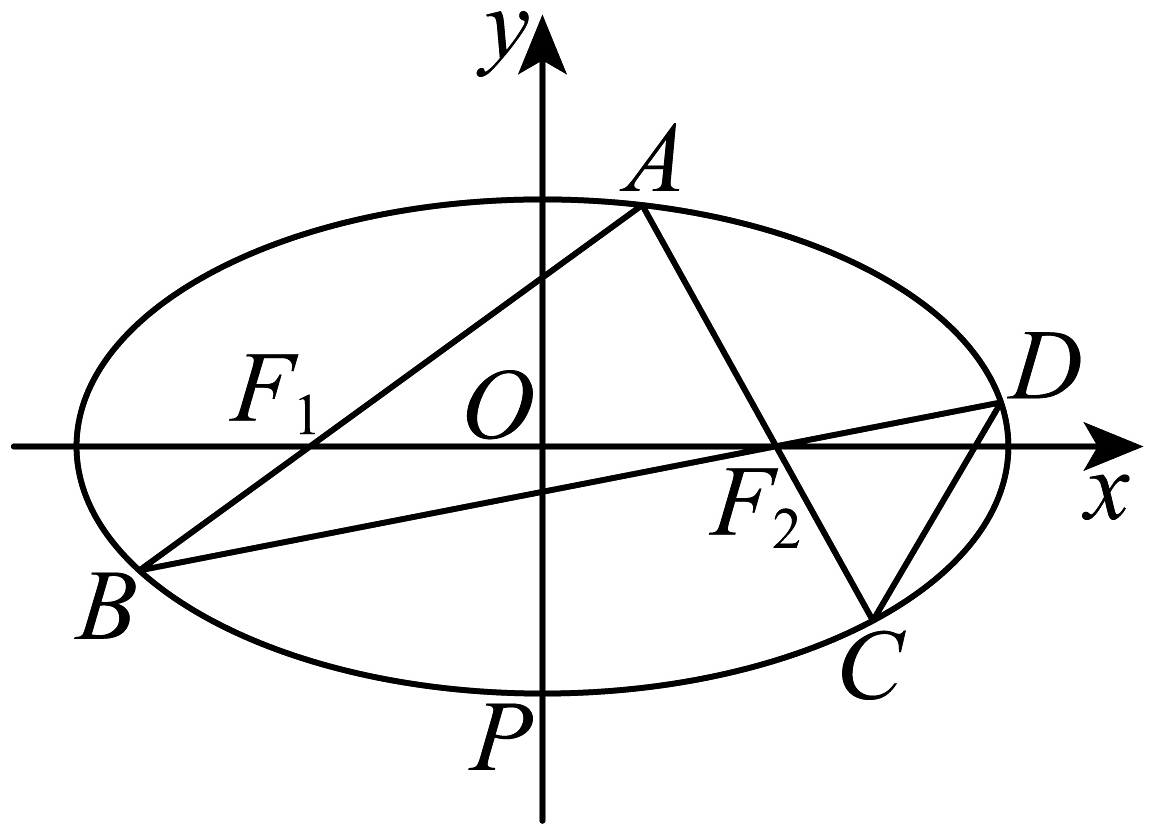(1)、求E的方程；

(2)、证明：直线CD过定点．

查看解析
17、某校为了解本校学生课间进行体育活动的情况，随机抽取了50名男生和50名女生，通过调查得到如下数据：50名女生中有10人课间经常进行体育活动，50名男生中有20人课间经常进行体育活动．

(1)、请补全 $2 \times 2$ 列联表，试根据小概率值 $α = 0.05$ 的独立性检验，判断性别与课间经常进行体育活动是否有关联；
性别
体育活动
合计
课间不经常进行体育活动
课间经常进行体育活动
男
女
合计

(2)、以样本的频率作为概率的值，在全校的男生中任取4人，记其中课间经常进行体育活动的人数为 $X$ ，求 $X$ 的分布列、数学期望和方差．
附表：
$α$
0.1
0.05
0.01
0.005
0.001
$x_{α}$
2.706
3.841
6.635
7.879
10.828
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．

查看解析
18、若 ${(2 - x)}^{7} = a_{0} + a_{1} (1 + x) + a_{2} {(1 + x)}^{2} + \dots + a_{7} {(1 + x)}^{7}$ ，则 $a_{0} + a_{1} + a_{2} + \dots + a_{7}$ 的值为．

查看解析
19、我国5G技术研发试验在2016~2018年进行，分为5G关键技术试验、5G技术方案验证和5G系统验证三个阶段.2020年初以来，5G技术在我国已经进入高速发展的阶段，5G手机的销量也逐渐上升．某手机商城统计了2022年5个月5G手机的实际销量，如下表所示：
月份
2022年1月
2022年2月
2022年3月
2022年4月
2022年5月
月份编号x
1
2
3
4
5
销量y（部）
50
96
a
185
227
若y与x线性相关，且求得回归直线方程为 $\hat{y} =$ $45 x + 5$ ，则下列说法正确的是（）

A、 $a = 142$ B、 $y$ 与 $x$ 正相关 C、 $y$ 与 $x$ 的相关系数为负数 D、2022年7月该手机商城的5G手机销量约为365部

查看解析
20、若“ $\exists x \in [4, 6]$ ， $x^{2} - a x - 1 > 0$ ”为假命题，则实数 $a$ 的取值可以为（）

A、8 B、7 C、6 D、5

查看解析

上一页 598 599 600 601 602 下一页跳转

性别	体育活动		合计
性别	课间不经常进行体育活动	课间经常进行体育活动
男
女
合计

月份	2022年1月	2022年2月	2022年3月	2022年4月	2022年5月
月份编号x	1	2	3	4	5
销量y（部）	50	96	a	185	227

$α$	0.1	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828