版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、对于集合 $A$ ， $B$ 和全集 $U$ ， “ $A \cap (∁_{U} B) = \emptyset$ ”是“ $A \subseteq B$ ”的什么条件（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看解析
2、如图，①②③④中不属于函数 $y = 2^{x}$ ， $y = 3^{x}$ ， $y = {(\frac{1}{2})}^{x}$ 的一个是（）

A、① B、② C、③ D、④

查看解析
3、设 $a > 0$ ，且 $a \neq 1$ ，则下列运算中正确的是（）

A、 $a^{\frac{4}{3}} a^{\frac{3}{4}} = a$ B、 $a^{\log_{a} \sqrt{a}} = \frac{1}{2}$ C、 $\log_{a} 2 = - \log_{2} a$ D、 $\frac{\sqrt{a} \sqrt[3]{a} \sqrt[4]{a}}{{(\sqrt[6]{a})}^{5} a^{\frac{1}{4}}} = 1$

查看解析
4、若两条平行直线 $l_{1}$ ： $x - 2 y + m = 0$ 与 $l_{2}$ ： $2 x + n y - 6 = 0$ 之间的距离是 $2 \sqrt{5}$ ，则 $m + n$ 的可能值为（）

A、 $3$ B、 $- 17$ C、 $- 3$ D、 $17$

查看解析
5、从某小区抽取100户层民用户进行月用电量调查，发现他们的月用电量都在 $50 ~ 350 kW \cdot h$ 之间，进行适当分组后（每组为左用右开的区间），画出频率分布直方图如图所示，在被调查的用户中，月用电量落在区间 $[100, 300)$ 内的户数为．

查看解析
6、已知函数 $f (x) = \frac{1}{3^{x} + 3}$ ．

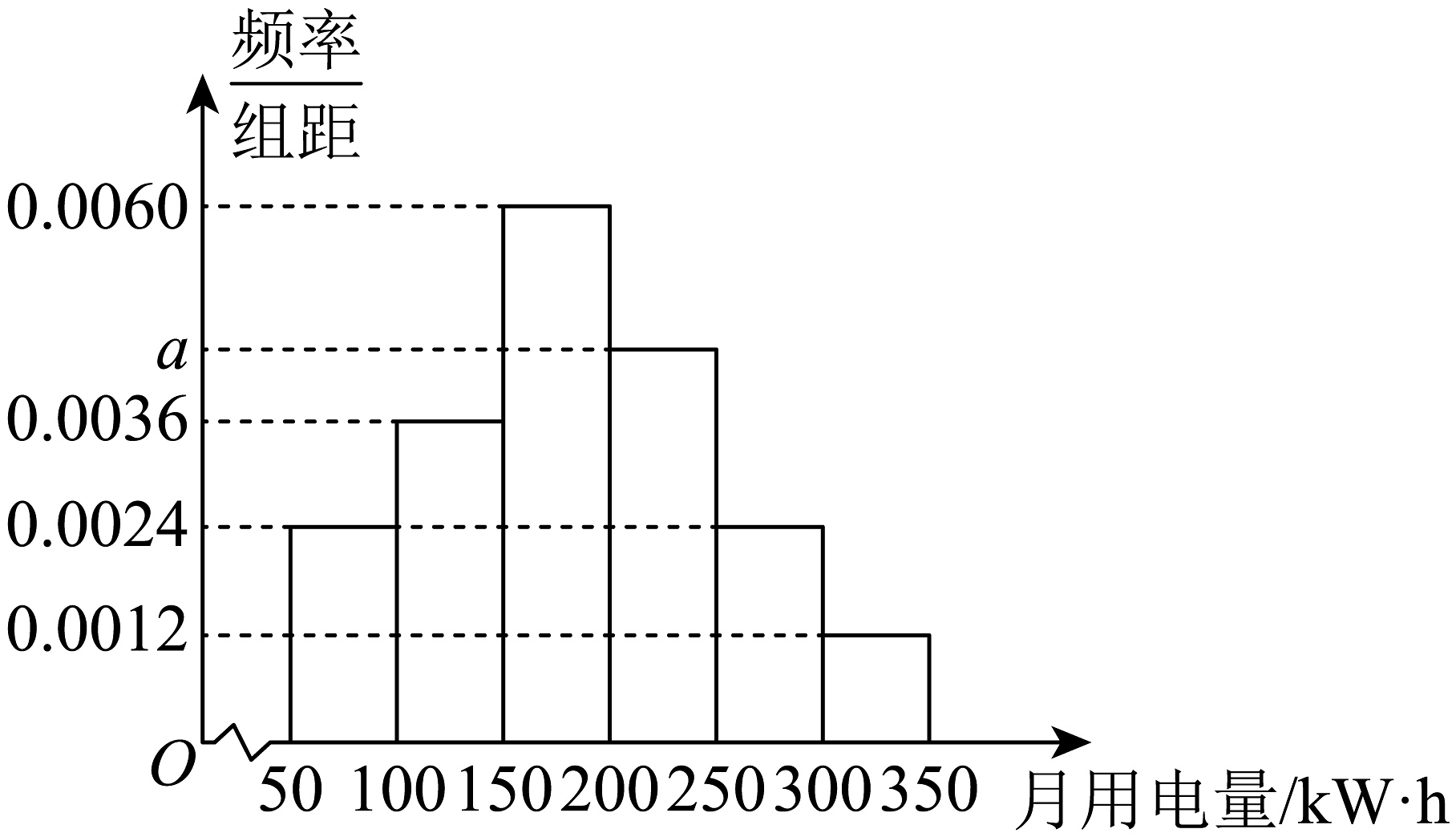
(1)、求 $f (0)$ 与 $f （ 2 ）$ ， $f (- 1)$ 与 $f （ 3 ）$ 的值；

(2)、由（1）中求得的结果，猜想 $f (x)$ 与 $f (2 - x)$ 的关系并证明你的猜想；

(3)、求 $f (- 2020) + f (- 2019) + \cdot \cdot \cdot + f (0) + f （ 1 ） + f （ 2 ） + \cdot \cdot \cdot + f (2021) + f (2022)$ 的值．

查看解析
7、函数 $y = 2^{x^{2} - 5 x - 6}$ 单调递减区间是（）

A、 $(- \infty, - 1)$ B、 $(\frac{5}{2}, + \infty)$ C、 $(- \infty, \frac{5}{2})$ D、 $(6, + \infty)$

查看解析
8、已知集合 $A = \{x |x^{3} - x - 7 \leq 0\}$ ， $B = \{y \in N |y = - x^{2} - 4 x - 2\}$ ，则 $A \cap B =$ （）

A、 $\{0\}$ B、 $\{0, 1, 2\}$ C、 $\{1, 2\}$ D、 $\{0, 1\}$

查看解析
9、已知平面四边形 $A B C D$ ， $A B = A D = 2$ ， $∠ B A D = 60 °$ ， $∠ B C D = 30 °$ ，现将 $△ A B D$ 沿 $B D$ 边折起，使得平面 $A B D ⊥$ 平面 $B C D$ ，此时 $A D ⊥ C D$ ，点 $P$ 为线段 $A D$ 的中点．

(1)、求证： $B P ⊥$ 平面 $A C D$ ；

(2)、若 $M$ 为 $C D$ 的中点，求 $M P$ 与平面 $B P C$ 所成角的正弦值；

(3)、在（2）的条件下，求二面角 $P - B M - D$ 的平面角的余弦值．

查看解析
10、如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = 4$ ， $A B = A D = 2$ ，点 $M$ 和点 $N$ 在棱 $C C_{1}$ 上，且 $C M = 2 C N = 2$ .

(1)、求证： $A M //$ 平面 $B D N$ ；

(2)、求证： $A_{1} C ⊥ D N$ .

查看解析
11、我校在2021年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组 $[75$ ， $80)$ ，第2组 $[80$ ， $85)$ ，第3组 $[85$ ， $90)$ ，第4组 $[90$ ， $95)$ ，第5组 $[95$ ， $100]$ ，得到的频率分布直方图如图所示，同时规定成绩在85分以上的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
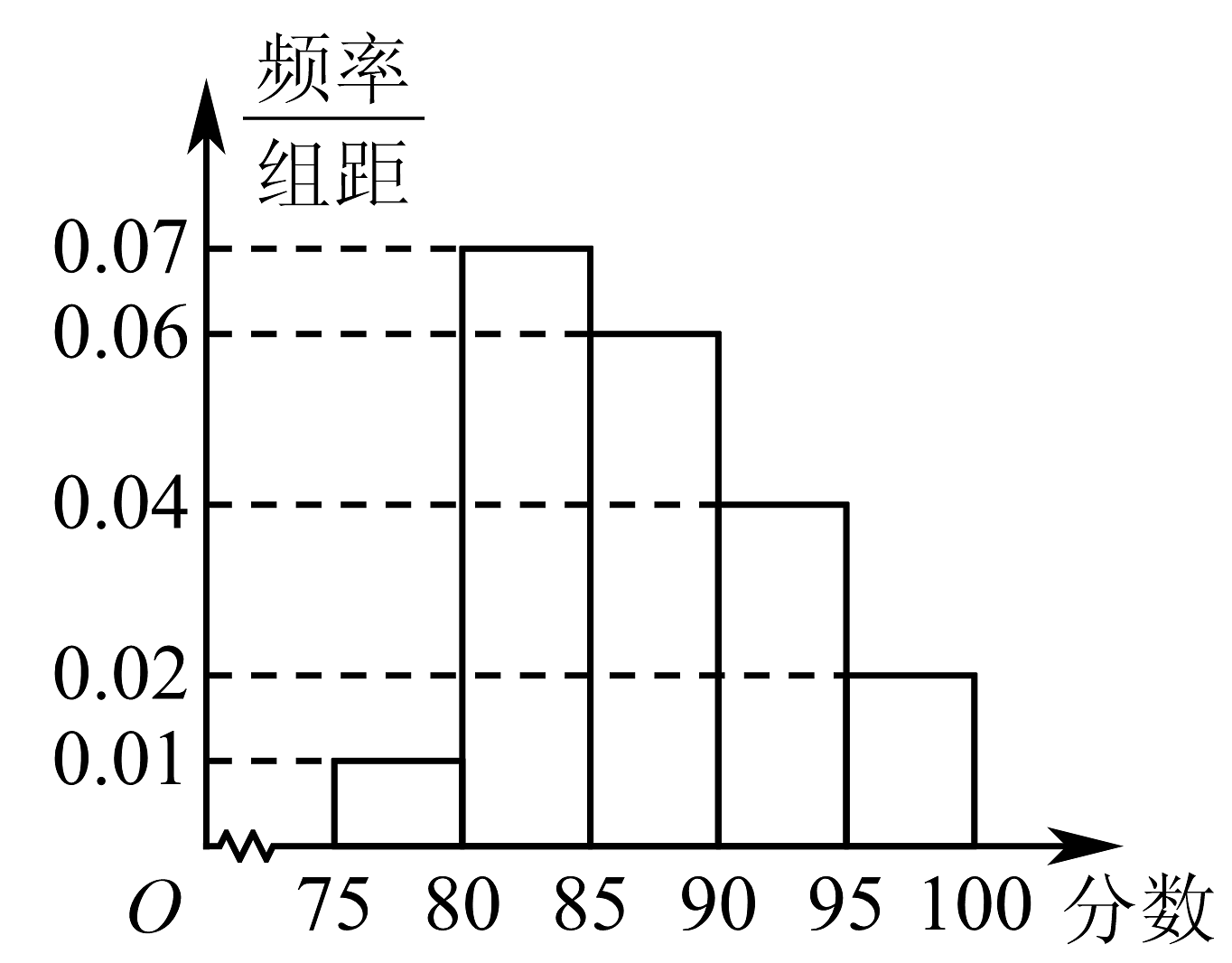
（1）根据样本频率分布直方图估计样本的中位数与平均数；
（2）如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？

查看解析
12、已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $(\vec{a} + \vec{b}) \cdot \vec{b} = 0$ ， $|\vec{a} + 4 \vec{b}| = 4$ ，则 $|\vec{a} + \vec{b}| + |\vec{b}|$ 的最大值为．

查看解析
13、如图所示，已知 $P A ⊥$ 平面 $A B C, ∠ A B C = 120^{\circ}, P A = A B = B C = 6$ ，则 $|\vec{P C}| =$ ．

查看解析
14、如图，在四边形 $A B C D$ 中， $△ A C D$ 和 $△ A B C$ 是全等三角形， $A B = A D$ ， $∠ A B C = 90 °$ ， $∠ B A C = 60 °$ ， $A B = 1$ ．下面有两种折叠方法将四边形 $A B C D$ 折成三棱锥．折法①；将 $△ A C D$ 沿着 $A C$ 折起，得到三棱锥 $D_{1} - A B C$ ，如图1．折法②：将 $△ A B D$ 沿着 $B D$ 折起，得到三棱锥 $A_{1} - B C D$ ，如图2．下列说法正确的是（）．

A、按照折法①，三棱锥 $D_{1} - A B C$ 的外接球表面积恒为 $4 π$ B、按照折法①，存在 $D_{1}$ 满足 $A B ⊥ C D_{1}$ C、按照折法②﹐三棱锥 $A_{1} - B C D$ 体积的最大值为 $\frac{\sqrt{3}}{8}$ D、按照折法②，存在 $A_{1}$ 满足 $A_{1} C ⊥$ 平面 $A_{1} B D$ ，且此时 $B C$ 与平面 $A_{1} B D$ 所成线面角正弦值为 $\frac{\sqrt{6}}{3}$

查看解析
15、某数学兴趣小组要测量一个球体建筑物的高度，已知点A是球体建筑物与水平地面的接触点（切点），地面上B，C两点与点A在同一条直线上，且在点A的同侧．若小明同学在B，C处分别测得球体建筑物的最大仰角为 $60 °$ 和 $20 °$ ，且 $B C = a$ 米，则该球体建筑物的高度为（）米．

A、 $\frac{a}{4 \cos 10 °}$ B、 $\frac{a}{2 \cos 10 °}$ C、 $\frac{a \sin 10 °}{2 \sin 40 °}$ D、 $\frac{a \sin 10 °}{\sin 40 °}$

查看解析
16、已知圆 $C$ 经过坐标原点，且圆心为 $(2, 0)$ ．

(1)、求圆 $C$ 的标准方程；

(2)、已知直线 $l : 3 x + 4 y - 1 = 0$ 与圆 $C$ 相交于 $A$ ， $B$ 两点，求弦长 $|A B|$ 的值；

(3)、过点 $P (4, - 4)$ 引圆 $C$ 的切线，求切线的方程．

查看解析
17、M是一个动点， $M M_{1}$ 与直线 $y = \frac{\sqrt{5}}{2} x$ 垂直，垂足 $M_{1}$ 位于第一象限， $M M_{2}$ 与直线 $y = - \frac{\sqrt{5}}{2} x$ 垂直，垂足 $M_{2}$ 位于第四象限，且 $\vec{M M_{1}} \cdot \vec{M M_{2}} = \frac{20}{81}$ ．

(1)、求动点M的轨迹方程E；

(2)、设 $A_{1} (- 2, 0)$ ， $A_{2} (2, 0)$ ，过点 $(3, 0)$ 的直线l与曲线E交于A，B两点（点A在x轴上方），P为直线 $A_{1} A$ ， $A_{2} B$ 的交点，当点P的纵坐标为 $\frac{5 \sqrt{10}}{6}$ 时，求直线l的方程．

查看解析
18、已知函数 $f (x) = \frac{1 + \ln x}{e^{x}}$ ．

(1)、求函数 $f (x)$ 在点 $(1, f (x))$ 处的切线方程；

(2)、求函数 $f (x)$ 的单调区间；

(3)、若 $f^{'} (x)$ 为 $f (x)$ 的导函数，设 $g (x) = (x^{2} + x) f^{'} (x)$ ．证明：对任意 $x > 0$ ， $g (x) < 1 + e^{- 2}$ ．

查看解析
19、某企业为了对一批新研发的产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据 $(x_{i}, y_{i}) (i = 1, 2, 3, 4, 5, 6)$ ，如下表所示：
试销单价x（百元）
1
2
3
4
5
6
产品销量y（件）
91
86
p
78
73
70
附：参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．
参考数据： $\bar{y} = \frac{1}{6} \sum_{i = 1}^{6} y_{i} = 80$ ， $\sum_{i = 1}^{6} x_{i} y_{i} = 1606$ ， $\sum_{i = 1}^{6} x_{i}^{2} = 91$ ．

(1)、求p的值；

(2)、已知变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（百元）的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ （计算结果精确到整数位）；

(3)、用 ${\hat{y}}_{i}$ 表示用正确的线性回归方程得到的与 $x_{i}$ 对应的产品销量的估计值．当销售数据 $(x_{i}, y_{i})$ 的残差的绝对值 $|{\hat{y}}_{i} - y_{i}| < 1$ 时，则将销售数据称为一个“有效数据”．现从这6组销售数据中任取2组，求“有效数据”个数 $ξ$ 的分布列和期望．

查看解析
20、如图，在四棱锥 $P - A B C D$ 中，四边形ABCD为正方形， $P A ⊥$ 平面ABCD， $A B = P A$ ， F是PB中点，

(1)、求证： $A F ⊥$ 平面PBC；

(2)、求二面角 $P - A C - F$ 的余弦值.

查看解析

上一页 580 581 582 583 584 下一页跳转

试销单价x（百元）	1	2	3	4	5	6
产品销量y（件）	91	86	p	78	73	70