相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、点是直线上一点,是直线的一个方向向量,则点到直线的距离是 .
-
2、关于空间向量,以下说法正确的是( )A、已知两个向量 , 且 , 则 B、已知 , 则在上的投影向量为 C、设是空间的一个基底,则也是空间的一个基底 D、若对空间中任意一点 , 有 , 则四点共面
-
3、如图,菱形边长为 , , 为边的中点,将沿折起,使到 , 连接 , 且 , 平面与平面的交线为 , 则下列结论中错误的是( )
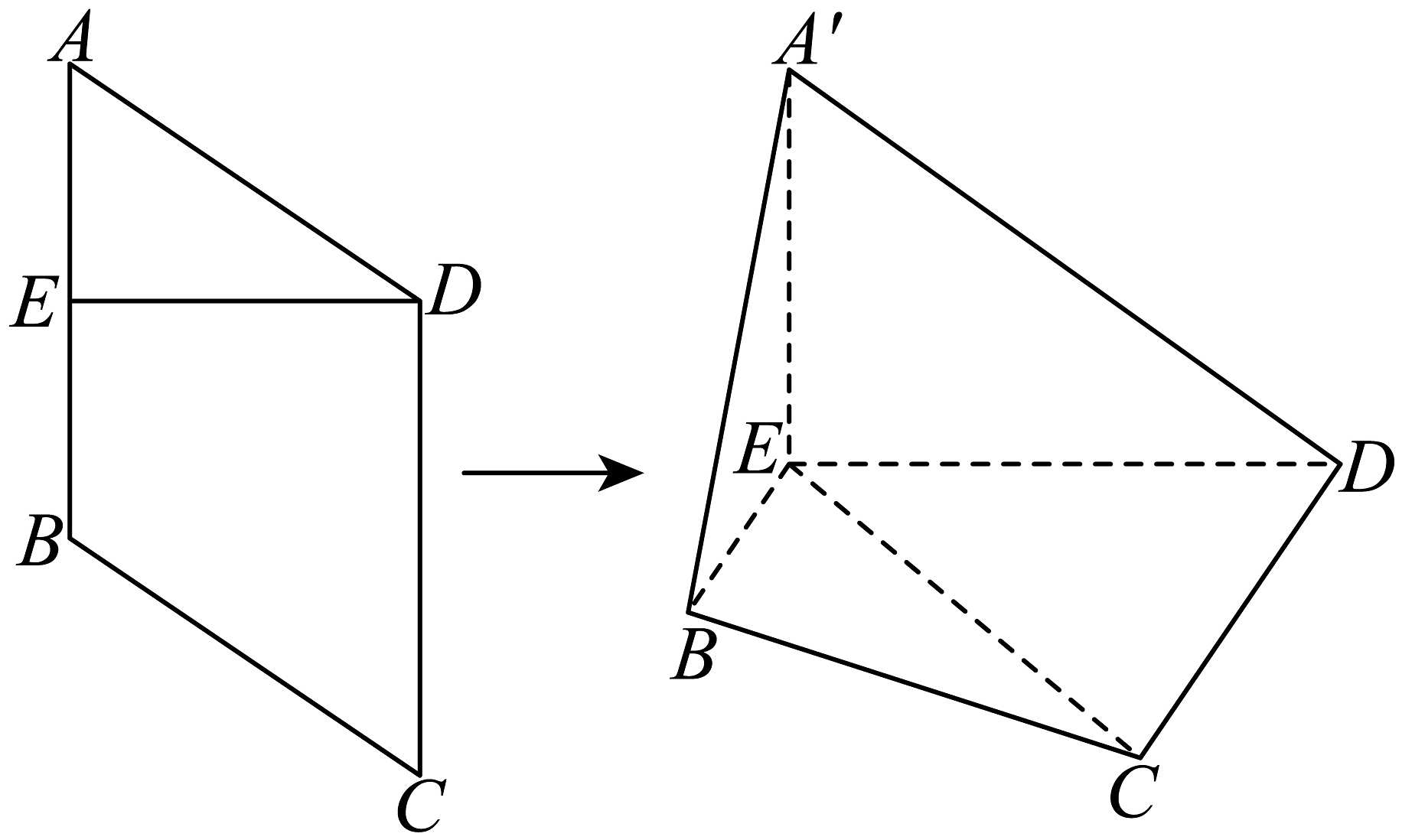 A、平面平面 B、 C、与平面所成角的余弦值为 D、二面角的余弦值为
A、平面平面 B、 C、与平面所成角的余弦值为 D、二面角的余弦值为 -
4、如图,设每个电子元件能正常工作的概率为 , 则电路能正常工作的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如右图在一个二面角的棱上有两个点 , , 线段分别在这个二面角的两个面内,并且都垂直于棱 , , 则这个二面角的度数为
 A、30° B、60° C、90° D、120°
A、30° B、60° C、90° D、120° -
6、如图所示,在平行六面体中, , , , M是的中点,N是线段上的点,且 , 用 , , 表示向量的结果是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图,在四棱锥中,底面为矩形,底面是的中点.
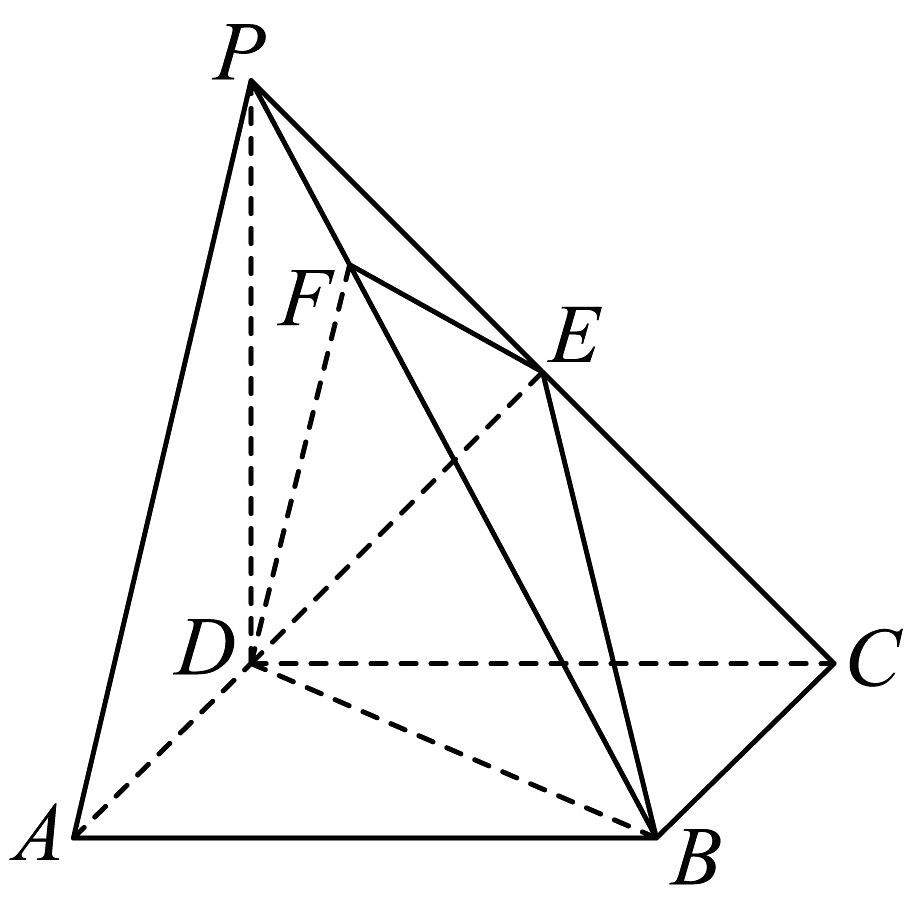 (1)、证明:平面;(2)、求平面与平面夹角的余弦值;(3)、在棱上是否存在一点 , 使直线与平面所成角的正弦值为 , 若存在,求出线段的长;若不存在,说明理由.
(1)、证明:平面;(2)、求平面与平面夹角的余弦值;(3)、在棱上是否存在一点 , 使直线与平面所成角的正弦值为 , 若存在,求出线段的长;若不存在,说明理由. -
8、现有标号依次为1,2,…,n的n个盒子,标号为1号的盒子里有2个红球和2个白球,其余盒子里都是1个红球和1个白球.现从1号盒子里取出2个球放入2号盒子,再从2号盒子里取出2个球放入3号盒子,…,依次进行到从号盒子里取出2个球放入n号盒子为止.(1)、当时,求2号盒子里有2个红球的概率;(2)、当时,求3号盒子里的红球的个数的分布列;(3)、记n号盒子中红球的个数为 , 求的期望 .
-
9、某企业协会规定:企业员工一周7天要有一天休息,另有一天的工作时间不超过4小时,且其余5天的工作时间均不超过8小时(每天的工作时间以整数小时计),则认为该企业“达标”.请根据以下企业上报的一周7天的工作时间的数值特征,判断其中无法确保“达标”的企业有( )A、甲企业:均值为5,中位数为8 B、乙企业:众数为6,中位数为6 C、丙企业:众数和均值均为5,下四分位数为4,上四分位数为8 D、丁企业:均值为5,方差为6
-
10、如图, , , 垂足分别为 , , 异面直线 , 所成角为 , , 点 , 点分别是直线 , 上的动点,且 , 设线段的中点为.
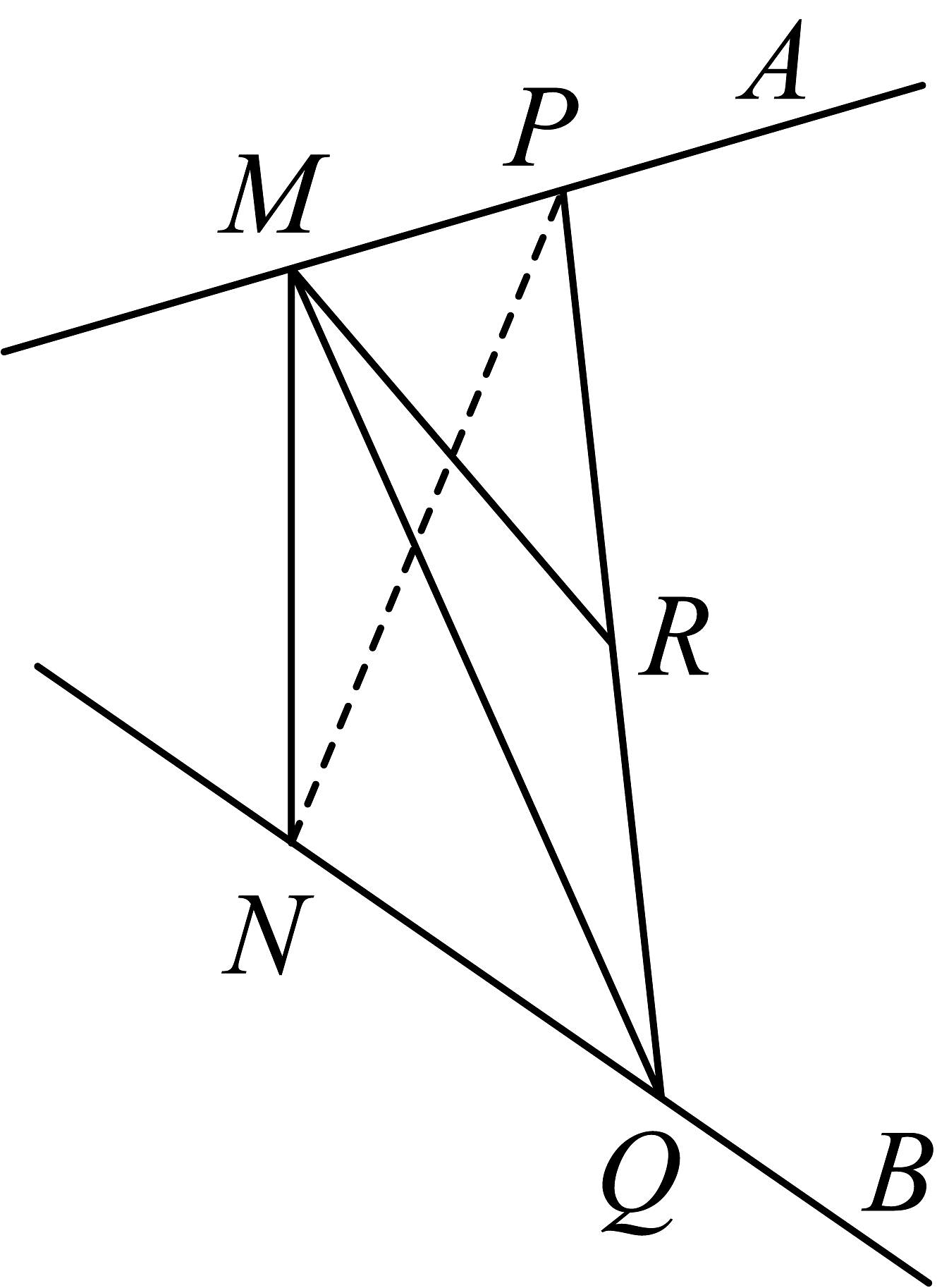 (1)、求异面直线与所成的角;(2)、求的取值范围;(3)、求四面体的体积的最大值.
(1)、求异面直线与所成的角;(2)、求的取值范围;(3)、求四面体的体积的最大值. -
11、已知圆: , 点 , 点是圆A上任意一点.线段的垂直平分线和半径相交于点 , 与圆A交于 , 两点,则当点在圆A上运动时,(1)、求点的轨迹方程;(2)、证明:直线是点轨迹的切线;(3)、求面积的最大值.
-
12、如图,四棱锥中,底面 , , , , .
 (1)、证明:平面;(2)、求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、求平面与平面夹角的余弦值. -
13、已知点与点关于直线:对称,圆:(),圆的半径为 , 且圆与圆交于 , 两点.(1)、求的取值范围;(2)、当时,求的面积.
-
14、记的内角 , , 的对边分别为 , , , 已知 ,(1)、求;(2)、过点作交于点 , 是的中点,连接.若 , 求的长度.
-
15、在棱长为2的正方体中, , 分别为棱 , 的中点,则四面体的外接球的表面积为.

-
16、已知圆: , 直线 , 若直线与圆相切,则.
-
17、已知椭圆: , 直线: , ( )A、若直线与椭圆有公共点,则 B、若 , 则椭圆上的点到直线的最小距离为 C、若直线与椭圆交于两点,则线段的长度可能为6 D、若直线与椭圆交于两点,则线段的中点在直线上
-
18、下列从总体中抽得的样本是简单随机抽样的是( )A、总体编号为1~75,在0~99之间产生随机整数.若或 , 则舍弃,重新抽取 B、总体编号为1~75,在0~99之间产生随机整数 , 除以75的余数作为抽中的编号.若余数为0,则抽中75 C、总体编号为6001~6879,在1~879之间产生随机整数 , 把作为抽中的编号 D、总体编号为1~712,用软件的命令“sample(1:712,50,replace=F”)得到抽中的编号
-
19、若直线:与直线:平行,则实数可能为( )A、1 B、2 C、3 D、4
-
20、已知函数 , , 则方程的实根个数是( )A、2 B、.3 C、4 D、5