相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、设空间两个单位向量 , 与向量的夹角都等于 , 则( )A、 B、 C、 D、
-
2、已知双曲线: , 过点的直线与双曲线交于 , 两点.若点为线段的中点,则直线的方程是( )A、 B、 C、 D、
-
3、已知函数 , , 且 , 则函数可能是( )A、 B、 C、 D、
-
4、从两位数中随机选择一个数,则它的平方的个位数字为1的概率是( )A、 B、 C、 D、
-
5、已知向量 , , 若 , 则( )A、 B、 C、1 D、2
-
6、若 , 则( )A、 B、 C、 D、
-
7、已知函数是定义在上的奇函数,若 , 且 , 都有成立,则不等式的解集为( )A、 B、 C、 D、
-
8、已知直椭圆柱体是指底面为椭圆,侧面与底面垂直的柱体.如图所示,直椭圆柱体的上下底面椭圆离心率为 , 高为椭圆短轴长度的 , 下底面长轴记为 , 上底面长轴记为 . 点为上一点,过点在下底面内作的垂线分别交下底面椭圆于点 , . 记 .
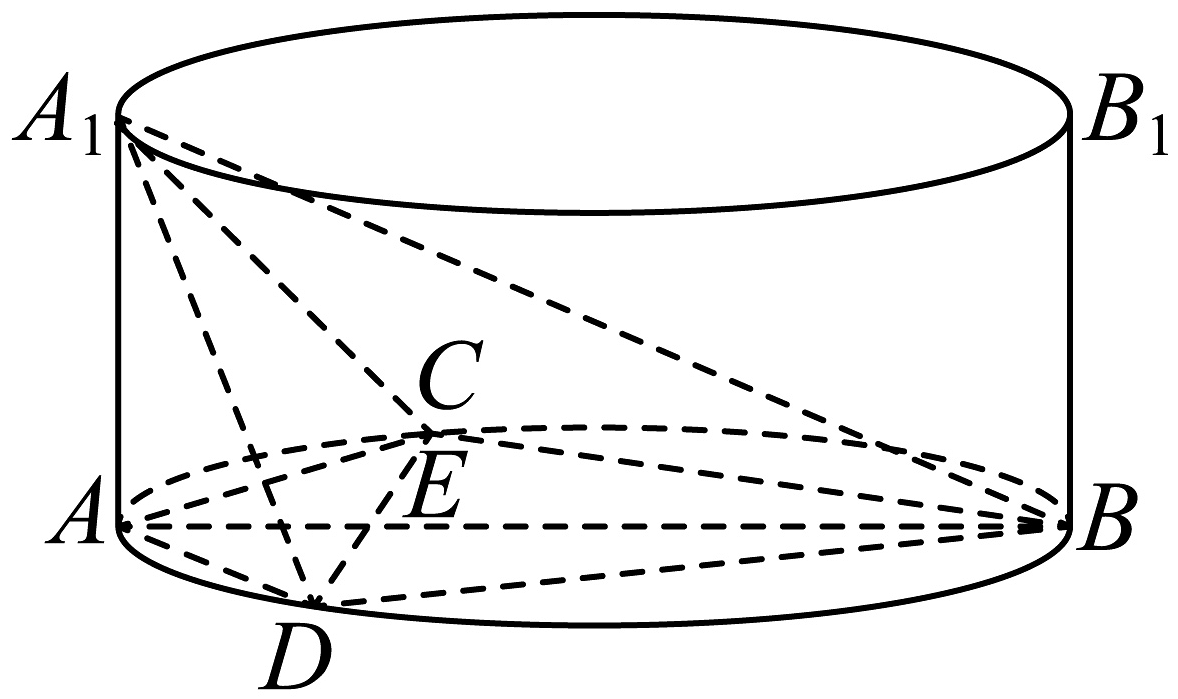 (1)、若平面平面 , 求及二面角的余弦值;(2)、若随变量的变化而变化,且 , . 记二面角的大小为 , 证明: .
(1)、若平面平面 , 求及二面角的余弦值;(2)、若随变量的变化而变化,且 , . 记二面角的大小为 , 证明: . -
9、某购物平台为了吸引更多的顾客在线购物,推出了和两个套餐服务,并在购物平台上推出了优惠券活动,顾客可自由选择和两个套餐之一,下图是该购物平台7天销售优惠券的情况(单位:千张)的折线图:
 (1)、由折线图可看出,可用回归模型拟合与的关系,请用相关系数加以说明;(2)、假设每位顾客选择套餐的概率为 , 选择套餐的概率为 , 其中包含一张优惠券,套餐包含两张优惠券,截止某一时刻,该平台恰好销售了张优惠券,设其概率为 , 求;(3)、记(2)中所得概率的值构成数列 , 求数列的最值.
(1)、由折线图可看出,可用回归模型拟合与的关系,请用相关系数加以说明;(2)、假设每位顾客选择套餐的概率为 , 选择套餐的概率为 , 其中包含一张优惠券,套餐包含两张优惠券,截止某一时刻,该平台恰好销售了张优惠券,设其概率为 , 求;(3)、记(2)中所得概率的值构成数列 , 求数列的最值.参考数据: , , ,
参考公式:相关系数
-
10、如图,在圆锥中,为圆锥底面的直径,为底面圆周上一点,点在线段上, , .
 (1)、证明:平面;(2)、若圆锥的侧面积为 , 求二面角的正弦值.
(1)、证明:平面;(2)、若圆锥的侧面积为 , 求二面角的正弦值. -
11、记内角 , , 的对边分别为 , , , 已知 .(1)、求;(2)、若 , , 求的周长.
-
12、如图,在的格子中,有一只蚂蚁从点爬到点,每次只能向右或向上移动一格,则从点爬到点的所有路径总数为 , 若蚂蚁只在下三角形(对角线及以下的部分所围成的三角形)行走,则从点到点的所有总路径数为 .

-
13、在的展开式中,常数项为 .
-
14、已知 , 则 .
-
15、我们知道,函数的图象关于坐标原点成中心对称图形的充要条件是函数为奇函数,有同学发现可以将其推广为:函数的图象关于点成中心对称图形的充要条件是函数为奇函数.已知是定义在上的可导函数,其导函数为 , 若函数是奇函数,函数为偶函数,则下列说法错误的是( )A、 B、 C、为奇函数 D、
-
16、过抛物线:的焦点作倾斜角为的直线交于 , 两点,经过点和原点的直线交抛物线的准线于点 , 则下列说法正确的是( ).A、 B、 C、以为直径的圆与轴相切 D、
-
17、已知随机变量服从正态分布,即 , 则( ).A、 B、 C、 D、
-
18、设函数 , 已知 , , 且的最小值为 , 则( )A、 B、 C、 D、
-
19、在平面直角坐标系中,点的坐标分别是 , , 直线 , 相交于点 , 且它们的斜率之积是 , 则点的轨迹方程为( ).A、 B、 C、 D、
-
20、若过点与圆相切的两条直线的夹角为 , 则( )A、 B、 C、 D、