相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知 , 则( )A、 B、0 C、 D、1
-
2、柳编技艺在我国已有上千年的历史,如今柳编产品已经选入国家非物质文化遗产名录.如图,若柳条编织的米斗可近似看作上底面圆半径为2,下底面圆半径为1,体积为的圆台,则该圆台的侧面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、要得到函数的图象,只需将函数的图象( )A、向左平移个单位长度 B、向右平移个单位长度 C、向左平移个单位长度 D、向右平移个单位长度
-
4、点满足向量 , 则点与的位置关系是( )A、点为线段的中点 B、点在线段延长线上 C、点在线段的延长线上 D、点不在直线上
-
5、已知 , 则在上的投影向量为( )A、 B、 C、 D、
-
6、已知复数 , 则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
7、定义:在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”,例如:数列1,3,5经过第一次“和扩充”后得到数列;第二次“和扩充”后得到数列.设数列经过次“和扩充”后得到的数列的项数为 , 所有项的和为.(1)、若已知数列 , 求;(2)、求不等式的解集;(3)、是否存在不全为0的数列 , 使得数列为等差数列?请说明理由.
-
8、设函数 .
(1)当时,函数与在处的切线互相垂直,求的值;
(2)若函数在定义域内不单调,求的取值范围;
(3)是否存在正实数 , 使得对任意正实数恒成立?若存在,求出满足条件的实数;若不存在,请说明理由.
-
9、已知的内角的对边分别为 , 且 .(1)、求边长和角;(2)、求的面积的最大值,并判断此时的形状.
-
10、如图所示,四棱锥中,四边形是矩形,平面平面 , , 点是线段的中点,点在线段上,且.
 (1)、求证:平面;(2)、若 , , 求平面与平面所成的角余弦值.
(1)、求证:平面;(2)、若 , , 求平面与平面所成的角余弦值. -
11、设是等比数列,是递增的等差数列,的前n项和为 , , , , .(1)、求与的通项公式(2)、求证:;(3)、设 , 求数列的前n项和.
-
12、的边的长分别为 , 且 , , , 则.
-
13、已知函数的部分图象如图所示,点 , 是该图象与轴的交点,过点的直线与该图象交于 , 两点,则的值为 .
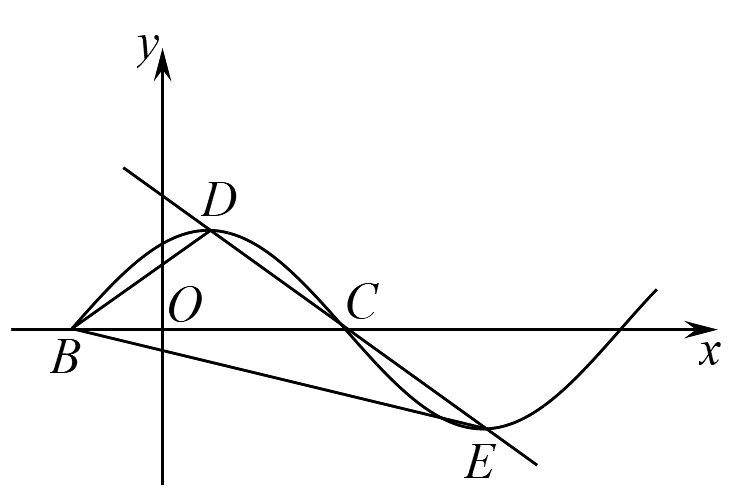
-
14、已知内角 , , 的对边分别为 , , , 为的重心, , , 则( )A、 B、 C、的面积的最大值为 D、的最小值为
-
15、设为正实数,且 , 已知函数 , 则使得该函数在上单调递减的充分条件可以是( )A、 B、 C、 D、
-
16、下列说法正确的有( )A、命题“ , ”的否定为“ , ” B、若 , 则 C、若幂函数在区间上是增函数,则或 D、在同一平面直角坐标系中,函数与函数的图象关于直线对称
-
17、已知 , 且满足 , 则( )A、 B、 C、 D、
-
18、已知函数 , 对任意 , 的最大值为4,若在上恰有两个极值点,则实数的取值范围是( )A、 B、 C、 D、
-
19、已知函数 , 其中 , 则下列选项中正确的是( )A、为奇函数 B、为偶函数 C、 D、
-
20、已知均为锐角,且 , 则( )A、 B、 C、 D、