版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、定义在 $(- 1, 1)$ 的函数 $f (x)$ 满足 $f (x) - f (y) = f (\frac{x - y}{1 - x y})$ ，且当 $- 1 < x < 0$ 时， $f (x) < 0$ ，则（）

A、 $f (x)$ 是奇函数 B、 $f (\frac{1}{5}) + f (\frac{1}{19}) = f (\frac{1}{4})$ C、 $f (\frac{1}{3}) + f (\frac{1}{4}) < f (\frac{1}{2})$ D、 $f (x)$ 在 $(- 1, 1)$ 上单调递增

查看解析
2、下列说法不正确的是（）

A、 $f (x)$ 的定义域为 $(- 1, 2)$ ，则 $f (2 x - 1)$ 的定义域为 $(- 3, 3)$ B、不等式 $2 k x^{2} + k x - \frac{3}{8} < 0$ 对一切实数 $x$ 恒成立的充分不必要条件是 $- 3 < k < 0$ C、一元二次不等式 $a x^{2} + b x + c > 0$ 的解集为 $(- 1, 3)$ ，则 $\frac{3 b^{2} - c^{2} + 1}{a}$ 有最小值 $2 \sqrt{3}$ D、若 $a > 0, b > 0, \frac{1}{a + 3 b} + \frac{1}{3 a + b} = 1$ ，则 $a + b$ 的最小值为1

查看解析
3、下列函数既是偶函数，又在 $(- \infty, 0)$ 上是减函数的是（）

A、 $y = x^{\frac{5}{4}}$ B、 $y = 3^{| x |}$ C、 $y = \lg (x^{2} + 1)$ D、 $y = - \frac{1}{4 x} + x$

查看解析
4、已知 $f (x) = \{\begin{matrix} {(a - 1)}^{x}, x \leq \frac{1}{2}, \\ x + \frac{a}{x} - 2, x > \frac{1}{2} \end{matrix} (a > 1)$ 的值域为 $D, D \subseteq [\frac{2}{5}, + \infty)$ ，则 $a$ 的取值范围是（）

A、 $(1, 2)$ B、 $[\frac{19}{10}, 2]$ C、 $(2, 5)$ D、 $[\frac{36}{25}, 2]$

查看解析
5、已知 $f (x) = m (x - 2 m) (x + m + 3), g (x) = 3^{x} - 3$ ，若命题“ $\forall x \in R, f (x) < 0$ 或 $g (x) < 0$ ”为真命题，则 $m$ 的取值范围是（）

A、 $(- 4, \frac{1}{2})$ B、 $(- 4, 0)$ C、 $(0, \frac{1}{2})$ D、 $(- \frac{1}{2}, 0)$

查看解析
6、若函数 $f (x) = \frac{4 x^{2} + x + 2}{2 x^{2} + 1}$ 的最大值为 $M$ ，最小值为 $N$ ，则 $M + N =$ （）

A、1 B、2 C、3 D、4

查看解析
7、现使用一架两臂不等长的天平称20g药品，操作方法如下：先将10g的砝码放在天平左盘中，取出一些药品放在天平右盘中，使天平平衡；再将10g的砝码放在天平右盘中，再取出一些药品放在天平左盘中，使得天平平衡．你认为两次实际称得的药品总重量（）

A、等于20g B、大于20g C、小于20g D、以上都有可能

查看解析
8、若集合 $A = \{x ||x + \frac{1}{2}| < \frac{5}{2}\}$ ， $B = \{x |\frac{5}{x - 3} \leq - 1\}$ ，则 $A \cup B =$ （）

A、 $(- 3, 3)$ B、 $(- 3, 3]$ C、 $(- 2, 2)$ D、 $[- 2, 2)$

查看解析
9、已知命题 $p : \forall x > 0, \sqrt{3 - x} > 0$ ，则命题 $p$ 的否定是（）

A、 $\forall x > 0, \sqrt{3 - x} \leq 0$ B、 $\exists x_{0} \leq 0, \sqrt{3 - x_{0}} \leq 0$ C、 $\exists x_{0} > 0, \sqrt{3 - x_{0}} \leq 0$ D、 $\forall x \leq 0, \sqrt{3 - x} \leq 0$

查看解析
10、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F$ ，右顶点为 $A$ ，上顶点为 $B$ ，点 $O$ 为坐标原点，线段 $O A$ 的中点恰好为 $F$ ，点 $F$ 到直线 $A B$ 的距离为 $\frac{\sqrt{21}}{7}$ ．

(1)、求 $C$ 的方程；

(2)、设点 $E$ 在直线 $x = 4$ 上，过 $F$ 作 $E F$ 的垂线交椭圆 $C$ 于 $M, N$ 两点．记 $△ M O E$ 与 $△ N O E$ 面积分别为 $S_{1}, S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值．

查看解析
11、如图，四棱锥 $P - A B C D$ 中， $P C ⊥$ 底面 $A B C D$ ，底面 $A B C D$ 为菱形， $∠ B A D = 60 °$ ， $A B = P C = 2, M, N$ 分别为 $P D, P B$ 的中点.

(1)、证明： $M N ⊥$ 平面 $P A C$ ；

(2)、求二面角 $C - P B - D$ 的正弦值.

查看解析
12、随机数表是人们根据需要编制出来的，由0，1，2，3，4，5，6，7，8，9这10个数字组成，表中每一个数都是用随机方法产生的，随机数的产生方法主要有抽签法、抛掷骰子法和计算机生成法．现有甲、乙、丙三位同学合作在一个正二十面体（如图）的各面写上0~9这10个数字（相对的两个面上的数字相同），这样就得到一个产生0~9的随机数的骰子．依次投掷这个骰子，并逐个记下朝上一面的数字，就能按顺序排成一个随机数表，若甲、乙、丙依次投掷一次，按顺序记下三个数，三个数恰好构成等差数列的概率为．

查看解析
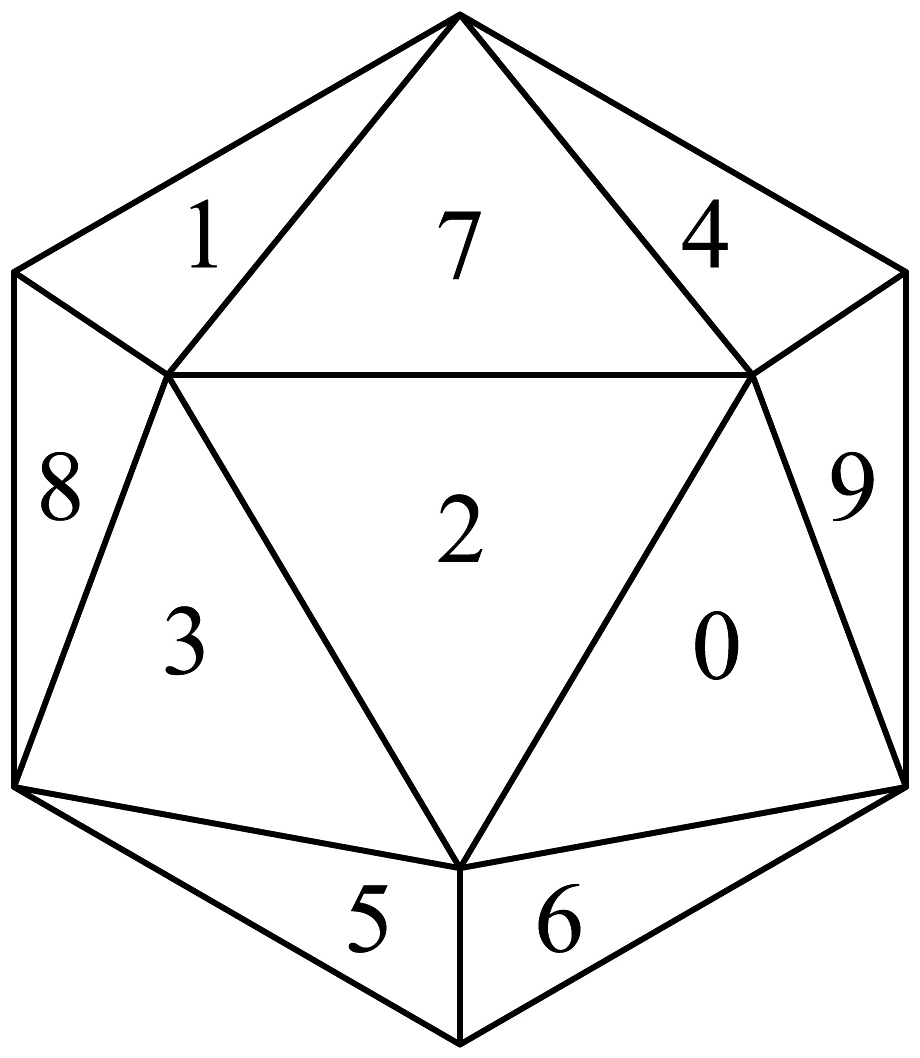
13、中国传世数学著作《九章算术》卷五“商功”主要讲述了以立体问题为主的各种形体体积的计算公式.例如在推导正四棱台（古人称方台）体积公式时，将正四棱台切割成九部分进行求解.下图（1）为俯视图，图（2）为立体切面图. $E$ 对应的是正四棱台中间位置的长方体， $B, D, H, F$ 对应四个三棱柱， $A, C, I, G$ 对应四个四棱锥.若这四个三棱柱的体积之和为12，四个四棱锥的体积之和为4，则该正四棱台的体积为.

查看解析
14、 ${(\sqrt{x} - \frac{a}{x^{2}})}^{5}$ 的展开式中的常数项是10，则 $a =$ .

查看解析
15、已知复数 $z = a - i (a \in R)$ ，且 $\frac{6 i}{z}$ 的虚部为3，则（）

A、 $a = 1$ B、 $|\frac{3}{z}| = 2 \sqrt{2}$ C、 $(z + 2) \cdot (1 - 3 i)$ 为纯虚数 D、 $\frac{2 + i}{z + 2}$ 在复平面内对应的点在第二象限

查看解析
16、已知抛物线 $C : y^{2} = 8 x$ ，圆 $F : {(x - 2)}^{2} + y^{2} = 4$ ，直线 $l : y = k (x - 2) (k \neq 0)$ 自上而下顺次与上述两曲线交于 $M_{1}, M_{2}, M_{3}, M_{4}$ 四点，则下列各式结果为定值的是

A、 $| M_{1} M_{3} | \cdot | M_{2} M_{4} |$ B、 $| F M_{1} | \cdot | F M_{4} |$ C、 $| M_{1} M_{2} | \cdot | M_{3} M_{4} |$ D、 $| F M_{1} | \cdot | M_{1} M_{2} |$

查看解析
17、已知曲线 $y = e^{x} (a x - \ln x)$ 在点 $(1, a e)$ 处的切线方程为 $y = k x$ ，则 $k =$ （）

A、 $- 1$ B、0 C、1 D、 $e$

查看解析
18、已知向量 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (3, λ)$ ，若 $\vec{a} + 2 \vec{b}$ 与 $2 \vec{a} - \vec{b}$ 平行，则实数 $λ$ 的值为（）

A、 $- \frac{2}{3}$ B、 $\frac{2}{3}$ C、6 D、 $- 6$

查看解析
19、已知集合 $A = {x | - 27 < x^{3} < 8}$ ， $B = {x | | x - 2 | \leq 3, x \in Z}$ ，则 $A \cap B =$ （）

A、 $\{- 1, 0\}$ B、 $\{0, 1\}$ C、 $\{- 1, 0, 1\}$ D、 $\{0, 1, 2\}$

查看解析
20、已知函数 $f (x) = \frac{1}{2} a x^{2} - (2 a + 1) x + 2 \ln x + 4 a (a > 0)$ .

(1)、求 $f (x)$ 的单调区间；

(2)、设 $g (x) = x^{2} - 2 x$ ，若对任意 $x_{1} \in (0, 2]$ ，均存在 $x_{2} \in (0, 2]$ ，使得 $f (x_{1}) < g (x_{2})$ ，求实数 $a$ 的取值范围.

查看解析

上一页 525 526 527 528 529 下一页跳转