相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知在正方体的棱长为2,点E,F分别是直线与上的点,则线段EF长度的最小值为( )A、 B、 C、 D、2
-
2、已知菱形中, , 沿对角线AC折叠之后,使得平面平面 , 则二面角的余弦值为( )
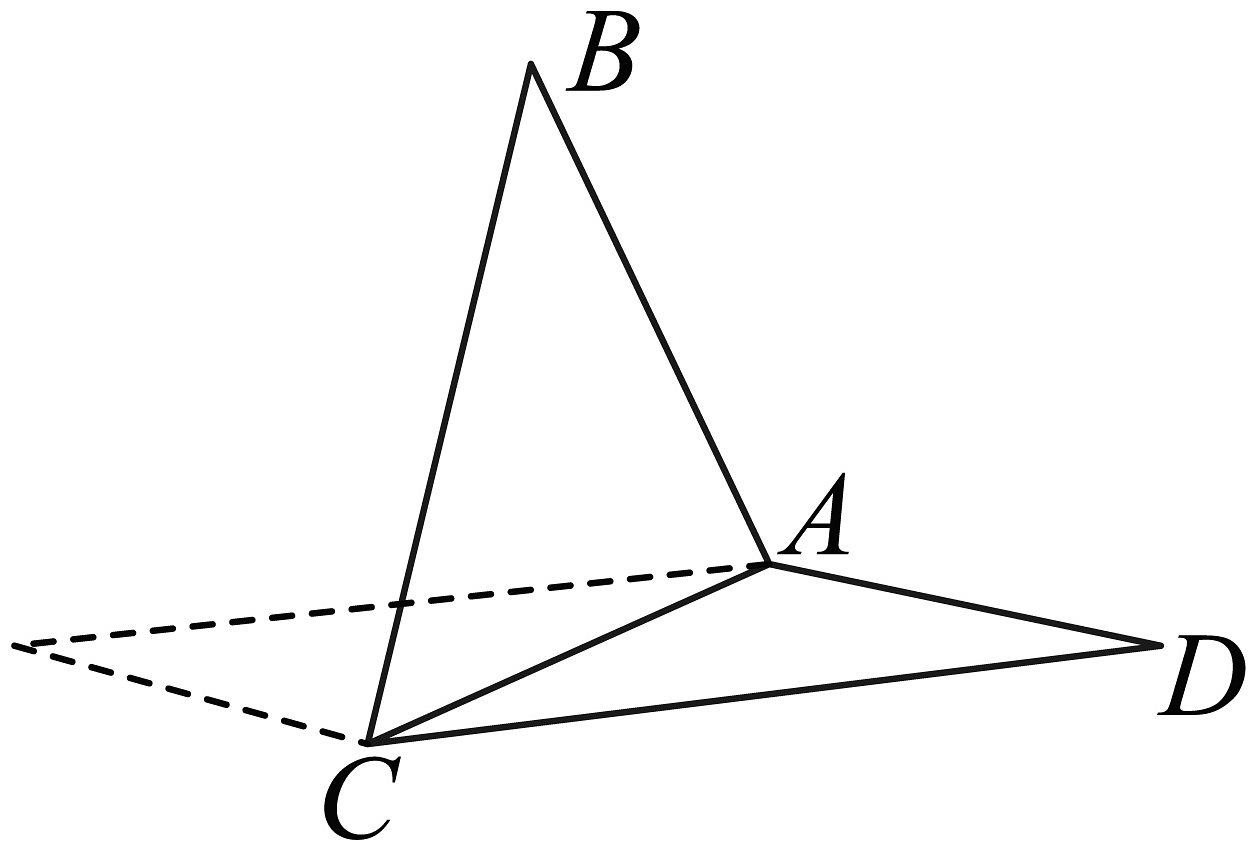 A、2 B、 C、 D、
A、2 B、 C、 D、 -
3、已知平面内有一个点 , 平面的一个法向量是 , 则下列点中,在平面内的是( )A、 B、 C、 D、
-
4、甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,设“甲中靶”,“乙中靶”,则( )A、A与B,A与 , 与B,与都相互独立 B、与是对立事件 C、 D、
-
5、如图,在斜三棱柱中,为的中点,为上靠近的三等分点,设 , , , 则用 , , 表示为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知向量 , , , 若 , , 共面,则( )A、2 B、3 C、 D、
-
7、若函数 , 的角 , , 的对边分别为 , , , 且.
(1)当取最大值时,判断的形状;
(2)在中,为边的中点,且 , , 求的长.
-
8、如图,为矩形,为梯形,平面平面 , , , .
 (1)、若为中点,求证:平面;(2)、求直线与直线所成角的大小;(3)、设平面平面 , 试判断与平面能否垂直?并求平面与平面所成锐二面角的大小.
(1)、若为中点,求证:平面;(2)、求直线与直线所成角的大小;(3)、设平面平面 , 试判断与平面能否垂直?并求平面与平面所成锐二面角的大小. -
9、已知四棱锥A—BCDE,AB=BC=AC=BE=1,CD=2BE=2,CD面ABC,BE∥CD,F为AD的中点.
 (1)、求证:EF∥面ABC;(2)、求四棱锥A—BCDE的体积,
(1)、求证:EF∥面ABC;(2)、求四棱锥A—BCDE的体积, -
10、在中,内角A,B,C所对边的长分别为a,b,c,且满足.(1)、求A;(2)、若 , , AD是的中线,求AD的长.
-
11、已知向量(1)、向量夹角的余弦值;(2)、若向量与垂直,求实数k的值;(3)、若向量 , 且与向量平行,求实数k的值.
-
12、如图,在中,是的中点,点在上,且与交于点 , 设.
 (1)、求的值;(2)、当时,求的值.
(1)、求的值;(2)、当时,求的值. -
13、中国有悠久的金石文化,印信是金石文化的代表之一.如下图的印信,可以看成是将一个棱长等于2cm的正方体截去8个一样的四面体之后得到的,则该印信的所有棱长之和等于cm,该印信的表面积等于.

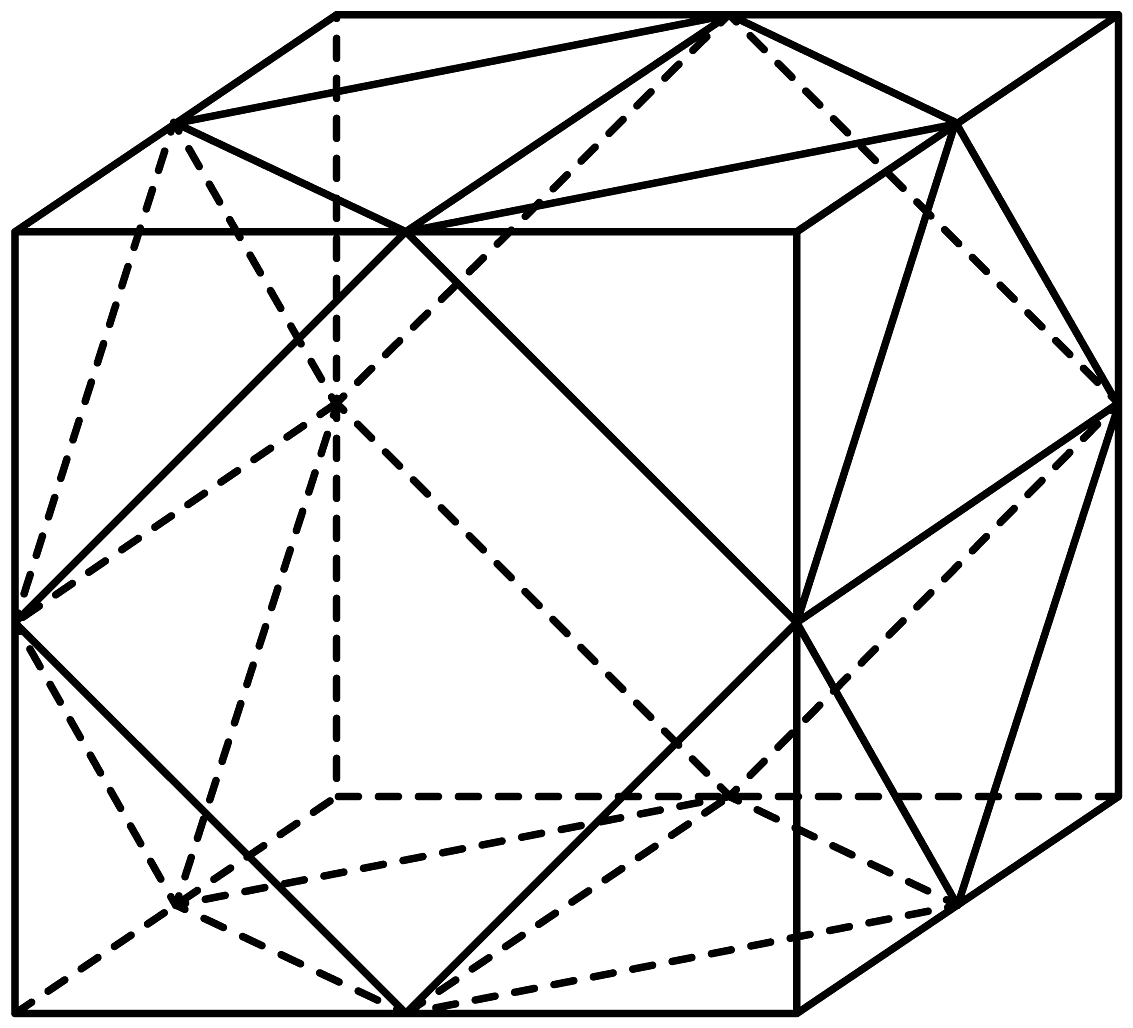
-
14、已知圆锥的侧面展开图是一个半径为的半圆,则圆锥的底面半径为;若该圆锥的顶点及底面圆周在球O的表面上,则球O的体积为.
-
15、是关于的方程的根, .
-
16、若 , , 则线段AB的靠近B的三等分点P的坐标为.
-
17、如图,在边长为2的正方形中,E、F分别是、的中点.若沿SE、SF及EF把这个正方形折成一个四面体,使、、三点重合,重合后的点记为G,则( )
 A、 B、点G到平面SEF的距离为 C、三棱锥的外接球表面积为 D、二面角等于
A、 B、点G到平面SEF的距离为 C、三棱锥的外接球表面积为 D、二面角等于 -
18、锐角△ABC中,内角A,B,C所对边分别为a,b,c,且 , 下列结论正确的是( )A、A=2B B、B的取值范围为 C、的取值范围为 D、的取值范围为
-
19、如图,直三棱柱的底面为直角三角形, , , , P是上一动点,则的最小值为( )
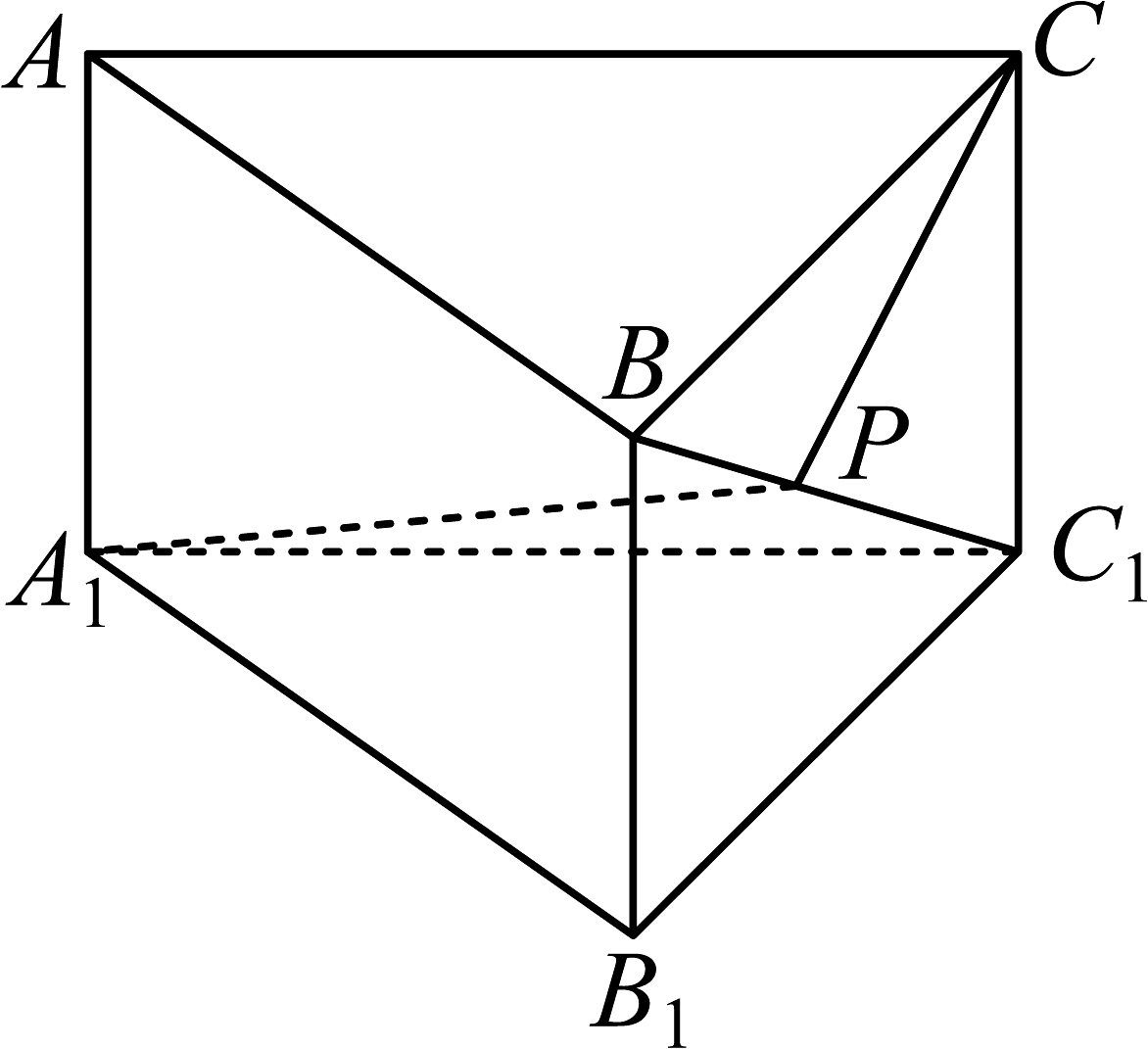 A、 B、 C、 D、
A、 B、 C、 D、 -
20、为捍卫国家南海主权,我国海军在南海海域进行例行巡逻,某天,一艘巡逻舰从海岛A出发,沿南偏东75°的方向航行到达海岛B,然后再从海岛B出发,沿北偏东45°的方向航行了海里到达海岛C.若巡逻舰从海岛A以北偏东60°的航向出发沿直线到达海岛C,则航行路程AC(单位:海里)为( )A、 B、 C、 D、