-
1、如图①所示为一把折叠椅子,图②是椅子完全打开支稳后的侧面示意图,其中BC和AD表示两根较粗的钢管,EG表示座板平面,EG,BC相交于点F,MN表示地面所在的直线, , EG距MN的高度为32cm, , , , .求两根较粗钢管BC和AD的长.(参考数据: , , , , , )

-
2、圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.(1)、从π的小数部分随机取出一个数字,估计数字是6的概率为.(2)、某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表的方法求解)
-
3、图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点.点A,B,C,D,E,O均在格点上.图①中已画出四边形ABCD,图②中已画出以OE为半径的☉O.只用无刻度的直尺,在给定的网格中按要求画图.
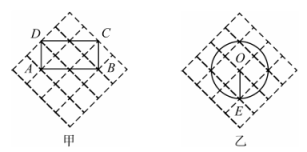 (1)、在图①中,画出四边形ABCD的一条对称轴.(2)、在图②中,画出经过点E的☉O的切线.
(1)、在图①中,画出四边形ABCD的一条对称轴.(2)、在图②中,画出经过点E的☉O的切线. -
4、解方程:(x+4)2=2(x+4)
-
5、(1)、计算:.(2)、化简:
-
6、如图,现有正方形纸片ABCD,点E,F分别在边AB,BC上.沿垂直于EF的直线折叠得到折痕MN,点B,C分别落在正方形所在平面内的点B',C'处,然后还原.
 (1)、若点N在边CD上,且∠BEF=α,则∠C'NM=.(用含α的式子表示)(2)、再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D'处,然后还原.若点D'在线段B'C'上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为.
(1)、若点N在边CD上,且∠BEF=α,则∠C'NM=.(用含α的式子表示)(2)、再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D'处,然后还原.若点D'在线段B'C'上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为. -
7、数学知识在生产和生活中被广泛应用,下列实例所运用的最主要的几何知识,说法正确的是.(填序号)
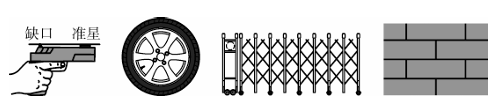
①射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”;
②车轮做成圆形,应用了“圆是中心对称图形”;
③学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”;
④地板砖可以做成矩形,应用了“矩形对边相等”.
-
8、如图所示,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若母线长l为8cm,扇形的圆心角θ=90°,则圆锥的底面圆半径r为cm.

-
9、如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,BD是边AC上的高.点E,F分别在边AB,BC上(不与端点重合),且DE⊥DF.设AE=x,四边形DEBF的面积为y,则y关于x的函数图象为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
10、抛物线y=-x2+bx+c与x轴交于两点,其中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论中,正确的是( )A、b=2 B、b+c>1 C、b2+4c D、c<0
-
11、如图所示,在中, , BD,AC相交于点D, , , , 则的面积是( )
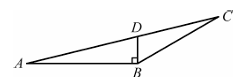 A、 B、 C、 D、
A、 B、 C、 D、 -
12、一元一次不等式组的解是( )A、 B、 C、 D、或
-
13、为发展学生的阅读素养,某校开设了《西游记》《三国演义》《水浒传》和《红楼梦》四本书的整本书阅读项目,甲、乙两名同学都通过抽签的方式从这四个阅读项目中随机抽取1个,则他们恰好抽到同一个阅读项目的概率是( )A、 B、 C、 D、
-
14、如图所示,BD平分∠ABC,CD∥AB.若∠BCD=70°,则∠ABD的度数为( )
 A、55° B、50° C、45° D、40°
A、55° B、50° C、45° D、40° -
15、下列运算中,正确的是( )A、 B、 C、 D、
-
16、2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与地球的最近距离约为55000000千米.55000000用科学记数法表示为( )A、55×106 B、5.5×107 C、5.5×108 D、0.55×108
-
17、如图所示为由长方体和圆柱组成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
18、已知△ABC,AB=AC=10,BC=16,P 是BC边上一点,连结AP.
 (1)、如图甲,沿线段AP 将△APC折叠,点C落在点D 处,AD 交边BC于 点E,
(1)、如图甲,沿线段AP 将△APC折叠,点C落在点D 处,AD 交边BC于 点E,①求证:△PED∽△AEB.
②若△ABE是等腰三角形,求PE的长.
(2)、如图乙,若∠APB=60°,△ABP 的外接圆交AC于点F,连结BF交AP 于点Q,求AQ的长. -
19、已知关于x的二次函数y=x2-bx+c(1)、若该函数的图象与x轴的交点坐标是(-1,0),(2,0),求b-2c的值.(2)、若该函数的图象的顶点纵坐标为3.
①用含b的代数式表示c.
②当1<x<m时,y的取值范围是3≤y<4,求c的取值范围.
-
20、在平面直角坐标系中,将任意两点横坐标之差的绝对值与纵坐标之差的绝对值中较大的值定义为这两点的“切比雪夫距离”.若点A(x1 ,y1 ), B(x2 ,y2 )两 点 间 的“切比雪夫距离”记作d(A,B),则d(A,B)=
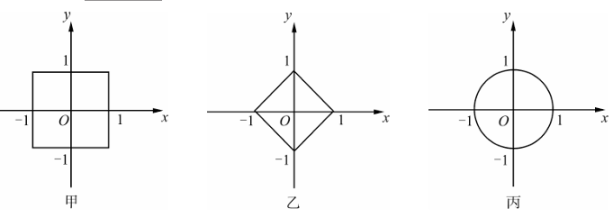 (1)、已知点M(2,1),N(-1,2),求d(M,N)的值.(2)、以下三个图形中,满足到原点O的切比雪夫距离不大于1的所有点构成的区域是.(填序号)(3)、设P 为直线l外一定点,Q为直线l上任意一点,定义d(P,Q)的最小值 为点P到直线l的“切比雪夫距离”,记作d(P,l). 求原点O到直线m∶y=-2x+2的切比雪夫距离d(O,m)的值.
(1)、已知点M(2,1),N(-1,2),求d(M,N)的值.(2)、以下三个图形中,满足到原点O的切比雪夫距离不大于1的所有点构成的区域是.(填序号)(3)、设P 为直线l外一定点,Q为直线l上任意一点,定义d(P,Q)的最小值 为点P到直线l的“切比雪夫距离”,记作d(P,l). 求原点O到直线m∶y=-2x+2的切比雪夫距离d(O,m)的值.