相关试卷

1、如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH，连结BE交线段AD于点M.若∠AMB=2∠BAF，AF=2，那么正方形EFGH的面积为.

查看解析
2、已知反比例函数 $y = - \frac{\sqrt{3}}{x}$ 图象上有两点A（a，b），B（ $\frac{1}{a}$ $, c),$ $0 < a < 1$ ，则b，c的大小关系是.

查看解析
3、已知扇形纸片OAB， $∠ A O B = 9 0^{°}$ ， $O A = 2$ ，将该扇形纸片沿OA方向平移得扇形 $O_{1} C D$ ，若 $O_{1}$ 恰好为OA中点，则阴影部分的面积为.

查看解析
4、随着科技发展，骑行共享单车这种“低碳”生活方式已融入人们的日常生活.据统计某市2024年4月份累计租车6500人次，租车量逐月增加，预计到6月份租车量达7600人次，求平均每个月的增长率.若设平均每月的增长率为x，根据题意可列方程为.

查看解析
5、一个不透明的袋子里有三张大小形状相同的卡片，分别写着数字4，5，6，从中任取一张，卡片上的数字为偶数的概率是.

查看解析
6、在平面直角坐标系中，直线 $y = k x + m$ 与抛物线 $y = x^{2}$ 相交于A（a，b）， $B (c, d)$ ，且 $0 < a < c$ ，则下列说法中，正确的是（）

A、若 $a = 1 - c$ ， $m$ 有最大值 $- \frac{1}{4}$ B、若 $a = 1 - c$ ， $m$ 有最小值 $- \frac{1}{4}$ C、若 $a = 1 - \frac{1}{2} c$ ， $m$ 有最大值 $- \frac{1}{2}$ D、若 $a = 1 - \frac{1}{2} c$ ， $m$ 有最小值 $- \frac{1}{2}$

查看解析
7、如图，在矩形ABCD中，E是AD上一点，连结BE，将△ABE沿BE折叠得△BEF，点F恰好在边CD上，过点A作AG//EF分别交BC，BF，BE于点G，P，Q.已知BC=3，当BG=2时，则折痕BE的长为（）

A、2 $\sqrt{3}$ B、4 C、3 $\sqrt{3}$ D、6

查看解析
8、现有一列数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $⋯$ ， $a_{20}$ ，满足任意相邻三个数的和为同一常数，当 $a_{2} = 2024$ ， $a_{7} = - 2020$ ， $a_{18} = - 1$ 时， $a_{1} + a_{2} + ⋯ + a_{20}$ 的值为（）

A、18 B、22 C、2024 D、2032

查看解析
9、如图，AB为☉O的直径，C为AB延长线上一点，过点C作☉O的切线CF，切点为E，作AD⊥CF于点D，连结AE，下列结论中，正确的是（）

A、B是OC中点 B、AE=CE C、AE²=AB·AC D、AE平分∠DAB

查看解析
10、已知直角三角形的两边长为3，4，则该直角三角形斜边上的中线长为（）

A、2或2.5 B、5或 $\sqrt{7}$ C、2.5或 $\sqrt{7}$ D、2.5或 $\frac{\sqrt{7}}{2}$

查看解析
11、甲、乙、丙、丁四人进行10次射击测试，他们的成绩的平均数相同，方差分别是 $s_{甲}^{2}$ =0.45， $s_{乙}^{2}$ =0.43， $s_{丙}^{2}$ =0.51， $s_{丁}^{2}$ =0.41，则这四人中，成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看解析
12、2023年嘉兴市的GDP为7062.45亿元，用科学记数法表示7062.45亿，正确的是（）

A、 $7.06245 \times 1 0^{11}$ B、 $0.706245 \times 1 0^{12}$ C、 $7.06245 \times 1 0^{10}$ D、 $70.6245 \times 1 0^{11}$

查看解析
13、如图所示为某几何体的三视图，该几何体可能是（）

A、圆柱 B、长方体 C、直五棱柱 D、五棱锥

查看解析
14、下列图标中，为轴对称图形的是（）

A、 B、 C、 D、

查看解析
15、如图，数轴上有A，B两点，表示的数分别为-3，2，则下列各数在数轴上对应的点，落在线段AB上的是（）

A、-4 B、-1.3 C、 $\sqrt{5}$ D、3

查看解析
16、△ABC内接于圆O，点I是△ABC的内心，连结AI并延长，交圆O于点D，连结BD，已知BC=6，∠BAC=α，

(1)、连结BI，CI，则∠BIC的度数为（用含有α的代数式表示）

(2)、求证：BD=DI.

(3)、连结OI，若 $t a n \frac{α}{2} = \frac{3}{4}$ ，求OI的最小值.

查看解析
17、已知二次函数 $y = x^{2} + b x + c$ $(b, c$ 为常数）的图象经过点 $A (- 2, 5)$ ，对称轴为直线 $x = - \frac{1}{2}$ .

(1)、求二次函数的表达式.

(2)、若点 $B (1, 7)$ 向上平移2个单位长度，向左平移 $m (m > 0)$ 个单位长度后，恰好落在 $y = x^{2} + b x + c$ 的图像上，求m的值.

(3)、当 $- 2 \leq x \leq n$ 时，二次函数 $y = x^{2} + b x + c$ 的最大值与最小值的差为 $\frac{9}{4}$ ，求n的取值范围.

查看解析
18、如图所示，在矩形ABCD中，点E，O分别为BC，BD的中点，过点A作AF平行于BD交EO的延长线于点F，连结CF交BD于点G.

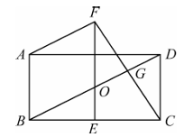(1)、求证：四边形ABOF为平行四边形.

(2)、若CF⊥BD，且AB=6，求OG的长.

查看解析
19、中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求，某小区增设了充电站，如图所示为矩形PQMN充电站的平面示意图，矩形ABCD是其中一个停车位.经测量，∠ABQ=60°，AB=5.4m，CE=1.6m，GH⊥CD，GH是另一个车位的宽，所有车位的长宽相同，按图示并列划定.根据以上信息回答下列问题（结果精确到0.1m，参考数据 $\sqrt{3}$ ≈1.73）：

(1)、求PQ的长.

(2)、该充电站有20个停车位，求PN的长.

查看解析
20、某兴趣小组为了了解本校男生参加课外体育锻炼情况，随机抽取本校300名男生进行了问卷调查，统计整理并绘制了如下两幅尚不完整的统计图.请根据以上信息解答下列问题：

(1)、课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为.

(2)、请补全条形统计图.

(3)、该校共有1200名男生，小明认为全校男生中，课外最喜欢参加的项目是乒乓球的人数约为1200× $\frac{27}{300}$ =108，请你判断这种说是否正确，并说明理由.

查看解析

上一页 969 970 971 972 973 下一页跳转