-
1、在平面直角坐标系中,平行四边形ABCD的对称中心是坐标原点,顶点A,B的坐标分别是(-1,1),(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是.
-
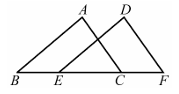
2、如图所示,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6,则BE的长是.
-
3、如图所示,在Rt△OAB中,∠AOB=30°,将△OAB绕点O按逆时针方向旋转100°得到△OA1B1 , 则∠A1OB的度数为.

-
4、已知二次函数的图像经过两点,则下列判断中,正确的是( )A、可以找到一个实数a,使得 B、无论实数a取什么值,都有 C、可以找到一个实数a,使得 D、无论实数a取什么值,都有
-
5、欧几里得的《几何原本》中给出了一个找线段的黄金分割点的方法:如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1与S2的比值为( )
 A、 B、 C、 D、1
A、 B、 C、 D、1 -
6、某班开展“用直尺和圆规作角平分线”的探究活动,各组展示的作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
7、如图所示,在四边形ABCD中 , , , , 把沿着AC翻折得到 , 若 , 则线段DE的长度是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、一张矩形纸片ABCD,已知AB=3,AD=2,小明按如图所示步骤折叠纸片,则线段DG的长为( )
 A、 B、 C、1 D、2
A、 B、 C、1 D、2 -
9、如图所示,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A'O'B,则下列四个图形中,正确的是( )
 A、
A、 B、
B、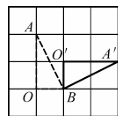 C、
C、 D、
D、
-
10、小美同学按如下步骤作四边形ABCD:①画∠MAN;②以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;③分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;④连结BC,CD,BD.若∠A=44̊,则∠CBD的大小是( )
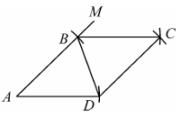 A、64̊ B、66̊ C、68̊ D、70̊
A、64̊ B、66̊ C、68̊ D、70̊ -
11、2024年6月5日,是二十四节气的芒种,二十四节气是中国古代劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
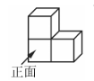
12、如图所示,由三个小正方体搭成的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
13、如图,已知△ABC内接于☉O,AB=BC,P为☉O上一点.
 (1)、如图甲,若点P在弧AMC上,连结BP交AC于点D.
(1)、如图甲,若点P在弧AMC上,连结BP交AC于点D.①求证:△BCD∽△BPC.
②若BD∶DP=1∶8,AP+PC=12,求AC的长.
(2)、如图乙,若点P在弧BC上,AP=6,BH⊥AP于点H,设PH=x,y=PH·PC.①求y关于x的函数表达式.
②求函数y的最大值.
-
14、已知二次函数的对称轴为 , 且.(1)、当时,求方程的根.(2)、当时,求证:.(3)、已知该二次函数的图象与x轴交于两点 , (点A在点B的左侧),与y轴的负半轴交于点C(0,c),若 , 且为直角三角形,求该二次函数的表达式.
-
15、如图,图甲是1个纸杯和6个叠放在一起的纸杯的示意图,量得1个纸杯的高为10厘米,6个叠放在一起的纸杯的高为14厘米.
 (1)、求4个叠放在一起的纸杯的高为多少厘米?(2)、若设x个叠放在一起的纸杯的高为y厘米(如图乙),并将这x个叠放在一起的纸杯按如图丙所示的方式放进竖立的方盒中,方盒的厚度不计.
(1)、求4个叠放在一起的纸杯的高为多少厘米?(2)、若设x个叠放在一起的纸杯的高为y厘米(如图乙),并将这x个叠放在一起的纸杯按如图丙所示的方式放进竖立的方盒中,方盒的厚度不计.①求y关于x的函数表达式.
②若竖立的方盒的高为33.5厘米,求x的最大值.
-
16、观察下面的等式:(1)、请写出的结果.(2)、按照上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数).(3)、试运用相关知识,推理说明你所得到的结论是正确的.
-
17、如图,已知四边形ABCD中,AB=CD,AE⊥BD于点E,CF⊥DB于点F,BE=CF.
 (1)、求证:△ABE≌△DCF.(2)、若点E是DF中点,CF=4,BC=5,求AD的长.
(1)、求证:△ABE≌△DCF.(2)、若点E是DF中点,CF=4,BC=5,求AD的长. -
18、某校为了推进拓展性课程建设,计划成立“文学”“机器人”“志愿者”“健美操”等多个社团,要求每名学生都自主选择其中一个社团,学生会组织调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成下面不完整的统计图表:
某校被调查学生选择社团意向统计表
社团
所占百分比
文学
40%
机器人
a
志愿者
b
健美操
6%
其它
16%
 (1)、求本次调查的学生总人数及a,b的值.(2)、将条形统计图补充完整.(3)、若该校共有1500名学生,试估计全校选择“志愿者”社团的学生人数.
(1)、求本次调查的学生总人数及a,b的值.(2)、将条形统计图补充完整.(3)、若该校共有1500名学生,试估计全校选择“志愿者”社团的学生人数. -
19、如图,在2×4的方格纸ABCD中,每个小方格的边长为1,已知格点P,请按要求完成以下问题.
 (1)、在图中画一个格点等腰三角形PEF,使得底边长为.(2)、在图中再找一个格点G,使得P,E,F,G四点构成平行四边形,则该平行四边形的面积为 .
(1)、在图中画一个格点等腰三角形PEF,使得底边长为.(2)、在图中再找一个格点G,使得P,E,F,G四点构成平行四边形,则该平行四边形的面积为 . -
20、(1)、计算:a(a+2)+(a-1)2.(2)、解不等式:4x+2≤x-1.