相关试卷

1、如图1，将一张平行四边形纸片 $O A B C$ 放置在平面直角坐标系中，点 $O$ 与原点重合， $O A$ 在 $x$ 轴上，点 $A (6, 0)$ ，点 $B, C$ 在第一象限，且 $A B = 4, ∠ A O C = 60 °$ ．

(1)、如图1，点 $B$ 的坐标为_______，点 $C$ 的坐标为_______．

(2)、如图2，若 $P$ 为 $x$ 轴的正半轴上的一个动点，过点 $P$ 作直线 $l ⊥ x$ 轴，沿直线 $l$ 折叠该纸片，折叠后点 $O$ 的对应点 $O^{'}$ 落在 $x$ 轴的正半轴上，点 $C$ 的对应点为 $C^{'}$ ．设 $O P = t$ ．
①若直线 $l$ 与边 $B C$ 相交于点 $Q$ ，将纸片折叠，当四边形 $P O^{'} C^{'} Q$ 与 $▱ O A B C$ 重叠部分为五边形时， $O^{'} C^{'}$ 与 $A B$ 相交于点 $E$ ．试用含有 $t$ 的式子表示线段 $B E$ 的长，并直接写出 $t$ 的取值范围；
②设折叠后重叠部分的面积为 $S$ ，当 $\frac{4}{3} \leq t \leq \frac{11}{2}$ 时，求 $S$ 的取值范围（直接写出结果即可）．

查看解析
2、定义：已知平面直角坐标系 $x O y$ 中有 $A$ ， $B$ 两点（点 $A$ 在点 $B$ 左侧）， $A B > 0$ ，且 $A B ∥ x$ 轴，若抛物线 $C : y = a x^{2} + b x + c (a \neq 0)$ 经过 $A$ ， $B$ 两点，则称抛物线 $C : y = a x^{2} + b x + c (a \neq 0)$ 是线段 $A B$ 的“共弦抛物线”．

(1)、若 $A (1, 3)$ ， $B (7, 3)$ ，线段 $A B$ 的一条“共弦抛物线” $C : y = a x^{2} + b x + c (a \neq 0)$ 的顶点 $N$ 的纵坐标为 $- 6$ ，求这个抛物线的解析式；

(2)、在（ $1$ ）的条件下，抛物线 $C$ 与 $x$ 轴相交于 $E$ ， $F$ 两点，求 $△ E F N$ 的面积；

(3)、若 $A B = 6$ ，线段 $A B$ 的“共弦抛物线” $C_{1} : y_{1} = 2 {(x + h)}^{2} + k$ 和 $C_{2} : y_{2} = a {(x + h)}^{2} + b$ 的顶点分别为点 $P$ ， $Q$ ，且点 $P$ ， $Q$ 距线段 $A B$ 的距离之和为 $21$ ，求 $a$ 的值．

查看解析
3、如图， $A B$ 是 $⊙ O$ 的直径，点 $C, D$ 在 $⊙ O$ 上， $B C ∥ O D$ ．

(1)、求证： $O D$ 平分 $∠ A O C$ ；

(2)、延长 $D O$ 交 $⊙ O$ 于点 $E$ ，连接 $C E$ 交 $O B$ 于点 $F$ ，过点 $B$ 作 $⊙ O$ 的切线交 $D E$ 的延长线于点 $P$ ，若 $\frac{E F}{C F} = \frac{5}{6}, P E = 1$ ，求 $P B$ 的长．

查看解析
4、电影《哪吒之魔童闹海》是一部大型的动画电影题材影片，该片以神话人物为背景，讲述一个感人的故事，影片于2025年1月开始上映后，深受人们的喜爱，票房过百亿．某影院开展“优惠”系列活动，对团体购买该电影票实行优惠，决定在原定零售票价基础上每张降价18元，这样按原定票价需花费5000元购买的门票张数，现在只花费了3200元．

(1)、求每张电影票的原定零售票价；

(2)、为了进一步回馈观众，该影院决定对网上购票的个人也采取优惠，原定零售票价经过连续两次降价后票价为每张 $40.5$ 元，求原定零售票价平均每次降价的百分率．

查看解析
5、如图，四边形 $A B C D$ 是菱形， $A E ⊥ C D$ 于点 $E$ ， $C F ⊥ A D$ 于点 $F$ ．

(1)、求证： $A F = C E$ ；

(2)、若 $A B = 2, ∠ A B C = 45 °$ ，求菱形 $A B C D$ 的面积．

查看解析
6、某校为提高学生体育运动能力，进一步增强学生的身体素质，现决定开设篮球、足球、排球、乒乓球、游泳5门运动课程．为了解学生需求，学校随机抽取部分学生进行调查（每人限选1门），并将调查结果绘制成如下两幅不完整的统计图．
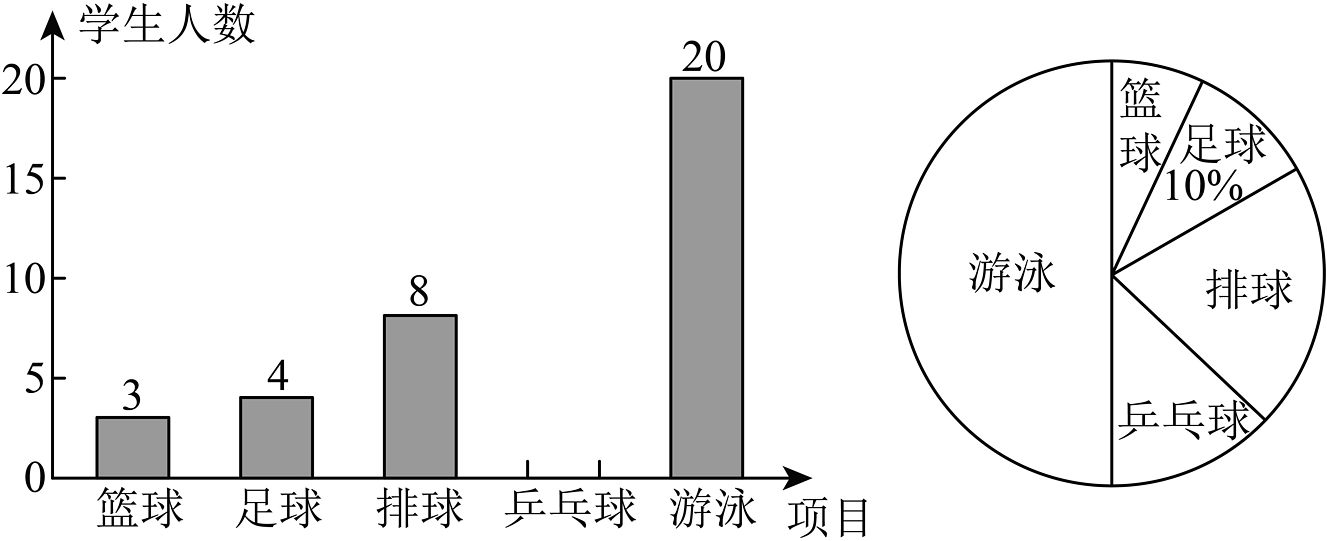
请你根据统计图提供的信息，解答下列问题：

(1)、本次调查的学生一共有________人；

(2)、扇形统计图中，“排球”所在扇形圆心角的度数为________；

(3)、若全校共有2200名学生，估计全校选择“乒乓球”的学生人数；

(4)、在选择“篮球”的3名学生中，有2名男生和1名女生，从这3名同学中随机抽取2名学生，求恰好抽到一名男生和一名女生的概率（用画树状图或列表的方法解答）．

查看解析
7、坐落于长沙望城区雷锋大道的雷锋双面雕塑，以雷锋的形象为艺术原型，突出表现雷锋舍己为人的伟大精神，为我们的城市增光添彩．某校数学社团的同学对该雕塑的高度进行了测量，如图， $C D ⊥ A C$ ，他们在 $A$ 处仰望雕塑 $C D$ 的顶部，测得仰角为 $30 °$ ，再往雕塑的方向前进 $34 m$ 至 $B$ 处，测得仰角为 $60 °$ ．（参考数据： $\sqrt{3} \approx 1.7$ ）

(1)、求证： $A B = D B$ ；

(2)、若学生的身高忽略不计，求该雕塑 $C D$ 的高度（结果精确到 $1 m$ ）．

查看解析
8、先化简，再求值： $(a + 3 - \frac{3 a + a^{2}}{a - 3}) \div \frac{a^{2} + 6 a + 9}{a - 3}$ ，其中 $a = \frac{3}{2}$ ．

查看解析
9、计算： ${(- \frac{1}{2})}^{- 2} + \sqrt{2} \tan 45 ° - |\sqrt{2} - 1| + \sqrt{8}$ ．

查看解析
10、如图，在已知的 $△ A B C$ 中，按如下步骤作图：
①分别以点 $B, C$ 为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧分别相交于点 $M, N$ ；
②作直线 $M N$ ，交 $A B$ 于点 $D$ ，连接 $C D$ ．
若 $C D = A C, ∠ A C D = 64 °$ ，则 $∠ A C B$ 的度数为．

查看解析
11、如图，将 $△ A B C$ 沿 $B C$ 边向右平移得到 $△ D E F$ ， $D E$ 交 $A C$ 于点 $G$ ，连接 $A D$ ．若 $S_{△ C E G} : S_{△ A D G}$ $= 4 : 9$ ， $B C = 10$ ，则 $C F$ 的值为．

查看解析
12、在某校举办的2024年秋季田径运动会上，参加初二女子跳高的7名运动员的成绩如下（单位：m）： $1.30$ ， $1.35$ ， $1.20$ ， $1.25$ ， $1.40$ ， $1.35$ ， $1.40$ ．这组数据的中位数是．

查看解析
13、我国古代数学名著记载：“今有牛十、羊四，直金三十八两；牛四、羊六，直金二十四两．问牛、羊各直金几何？”题目大意是： $10$ 头牛、 $4$ 只羊共 $38$ 两银子； $4$ 头牛、 $6$ 只羊共 $24$ 两银子，每头牛、每只羊各多少两银子？设 $1$ 头牛 $x$ 两银子， $1$ 只羊 $y$ 两银子，则可列方程组为．

查看解析
14、要使二次根式 $\sqrt{5 - 3 x}$ 有意义，则 $x$ 的取值范围是．

查看解析
15、 $2025$ 年某单位举行春节联欢会，其中有 $A, B, C, D$ 四个节目需要彩排．所有演员到场后节目彩排开始．一个节目彩排完毕，下一个节目彩排立即开始．每个节目的演员人数和彩排时长（单位： $\min$ ）如下表所示：
节目
$A$
$B$
$C$
$D$
演员人数
$12$
$2$
$12$
$1$
彩排时长
$25$
$8$
$20$
$8$
已知每位演员只参演一个节目．一位演员的候场时间是指从第一个彩排的节目彩排开始到这位演员参演的节目彩排开始的时间间隔（不考虑换场时间等其他因素）．若使这 $27$ 位演员的候场时间之和最小，则节目彩排的先后顺序为（）

A、 $A - B - C - D$ B、 $A - C - B - D$ C、 $C - A - B - D$ D、 $C - B - A - D$

查看解析
16、如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 切 $⊙ O$ 于点 $C$ ，连接 $A C$ ， $B C$ ，若 $∠ A B C = 26 °$ ，则 $∠ B C D$ 的度数为（）

A、 $64 °$ B、 $54 °$ C、 $52 °$ D、 $74 °$

查看解析
17、如图，在平面直角坐标系中，半径均为2个单位长度的半圆 $O_{1}, O_{2}, O_{3}, \dots$ 组成一条平滑的曲线，将一枚棋子放在原点 $O$ 处，第一步，棋子从点 $O$ 跳到点 $A_{1} (2, 2)$ ；第二步，从点 $A_{1}$ 跳到点 $A_{2} (4, 0)$ ；第三步，从点 $A_{2}$ 跳到点 $A_{3} (6, - 2)$ ；然后依次在曲线上向右跳动一步，则棋子跳到点 $A_{1013}$ 时的坐标为（）

A、 $(2026, 0)$ B、 $(2026, - 2)$ C、 $(2024, 0)$ D、 $(2026, 2)$

查看解析
18、正九边形的每一个内角的度数是（）

A、 $40 °$ B、 $140 °$ C、 $45 °$ D、 $135 °$

查看解析
19、不等式 $3 (3 - x) < 3 x - 3$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看解析
20、将一块等腰直角三角板按如图方式摆放，其中 $a ∥ b$ ， $∠ 2 = 155 °$ ，则 $∠ 1$ 的度数为（）

A、 $30 °$ B、 $25 °$ C、 $20 °$ D、 $15 °$

查看解析

上一页 949 950 951 952 953 下一页跳转

节目	$A$	$B$	$C$	$D$
演员人数	$12$	$2$	$12$	$1$
彩排时长	$25$	$8$	$20$	$8$