-
1、如图,为的直径,弦交于点M,且 , 若 , , 则的半径为( )
 A、 B、 C、3 D、4
A、 B、 C、3 D、4 -
2、二次函数的部分图象如图所示,下列说法正确的是( )
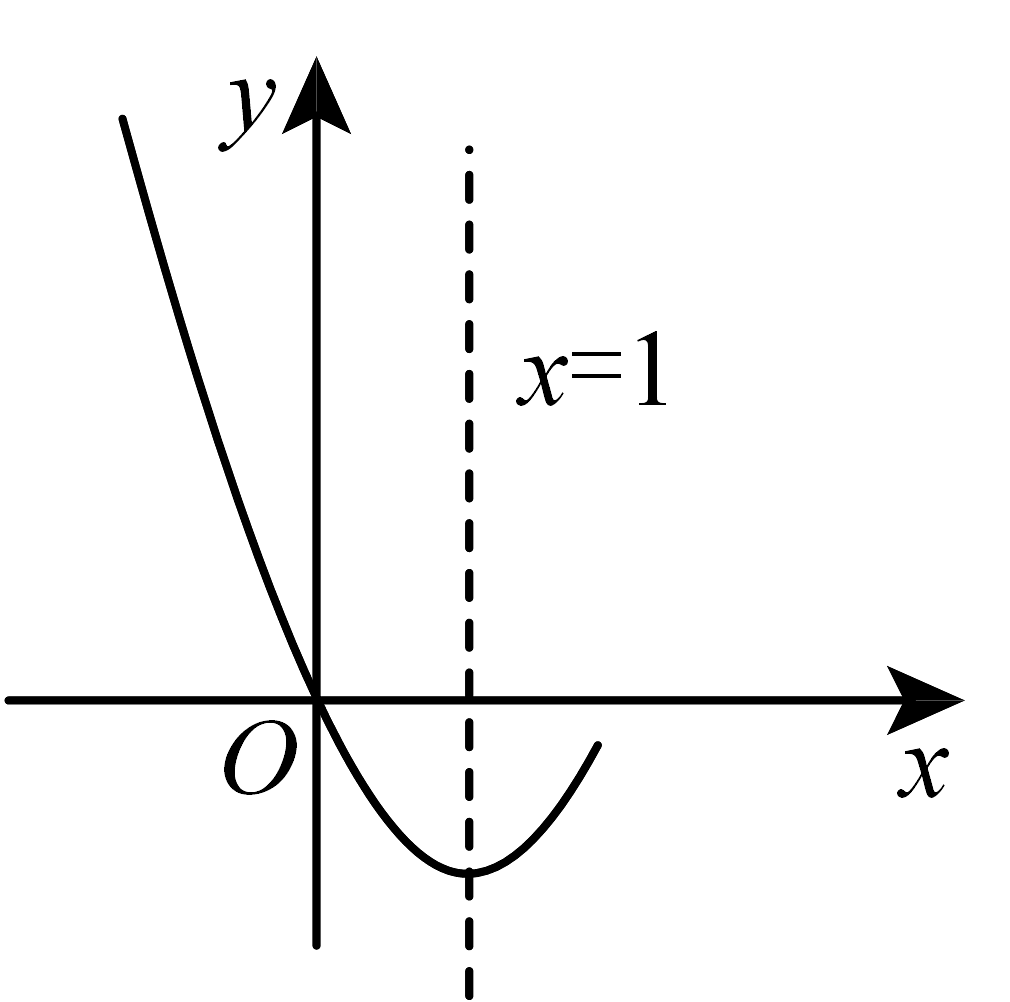 A、 B、 C、 D、
A、 B、 C、 D、 -
3、已知一元二次方程配方后可变形为 , 则的值为( )A、8 B、7 C、6 D、5
-
4、下列乐谱符号中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、综合与实践活动课上,老师让同学们以“折纸作的角”为主题开展数学活动.
【操作判断】
(1)①如图①,对折矩形纸片 , 使与重合,得到折痕 , 把纸片展平在上选一点P,沿折叠,使点A落在上的点M处,把纸片展平,连接 . 则______.
②如图②,在前面操作的基础上,延长与交于点N,则的形状是______.
【迁移探究】
(2)小明将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片按照(1)中的方式操作,并延长与交于点Q,连接 .
如图③,若改变点P在上的位置(点P不与点A,D重合),判断与的数量关系,并说明理由;
【拓展应用】
(3)在(2)的探究中,已知正方形的边长为 , 当P是边的三等分点时,求出的长.

-
6、问题呈现:对于任意正实数x、y,由于 , 所以有 , 于是 , 只有当时,才成立.也就是说,若为定值 , 则当时,有最小值 .
 (1)、若 , 则只有当_______时,有最小值______.(2)、数学思考:现有面积为1的矩形 , 直接写出其周长的最小值_______.(3)、拓展运用:如图,在平面直角坐标系中,已知 , , 点为第一象限内一动点,过P分别向坐标轴作垂线,分别交x、y轴于C、D两点,矩形的面积始终为12,设四边形的面积为S,当四边形的面积S最小时,试判断四边形为何种特殊形状的平行四边形,求出最小值并说明理由.
(1)、若 , 则只有当_______时,有最小值______.(2)、数学思考:现有面积为1的矩形 , 直接写出其周长的最小值_______.(3)、拓展运用:如图,在平面直角坐标系中,已知 , , 点为第一象限内一动点,过P分别向坐标轴作垂线,分别交x、y轴于C、D两点,矩形的面积始终为12,设四边形的面积为S,当四边形的面积S最小时,试判断四边形为何种特殊形状的平行四边形,求出最小值并说明理由. -
7、在四边形中,对角线相交于点 , E,F,G,H分别是的中点.
 (1)、求证:四边形是平行四边形;(2)、若 , 求证:四边形是菱形.
(1)、求证:四边形是平行四边形;(2)、若 , 求证:四边形是菱形. -
8、先阅读,再解答.由可以看出,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式,在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号,例如: . 请完成下列问题:(1)、的有理化因式是_____;_____.(2)、利用这一规律计算:的值.
-
9、已知一次函数的图象经过和两点.(1)、求这个一次函数的解析式;(2)、若点在这个函数图象上,求的值.
-
10、如图,在四边形中, , , , , .
 (1)、求证:(2)、求四边形的面积.
(1)、求证:(2)、求四边形的面积. -
11、已知直线 , 回答下列问题:(1)、与y轴交点A的坐标为_______.(2)、求与x轴的交点B的坐标;(3)、求线段的长度
-
12、拖拉机开始工作时,油箱中有油60L,每小时耗油5L.(1)、写出油箱中的余油量Q(L)与工作时间t(h)之间的函数关系式;(2)、写出自变量t的取值范围;(3)、拖拉机工作4小时后,油箱余油是多少?
-
13、如图,若输入的值为 , 则输出的结果 .

-
14、如图,矩形中,对角线相交于点 , 若 , , 则的长度为 .

-
15、如图,的对角线 , 交于点 , 平分 , 交于点E,且 , , 连接 . 下列结论:①为等边三角形;②;③;④ . 正确的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
16、一天,小明吃完晚饭出去散步,从家出发沿直线匀速走了20分钟到达离家900米的书店,看了10分钟的书后,原路原速返回家,则表示小明离家距离与时间之间关系的图象是( )A、
 B、
B、 C、
C、 D、
D、
-
17、如图,菱形的对角线、相交于点 , 是的中点,且 , 则的长是( )
 A、2.5 B、3 C、4 D、5
A、2.5 B、3 C、4 D、5 -
18、以下列各组数为边长,可以构成直角三角形的是( )A、 B、 C、 D、
-
19、如图,抛物线与轴交于 , 两点,与轴交于点 , 对称轴为直线 . 点是抛物线上的一个动点,设它的横坐标为 . 过点作轴,与交于点 , 连接 , .
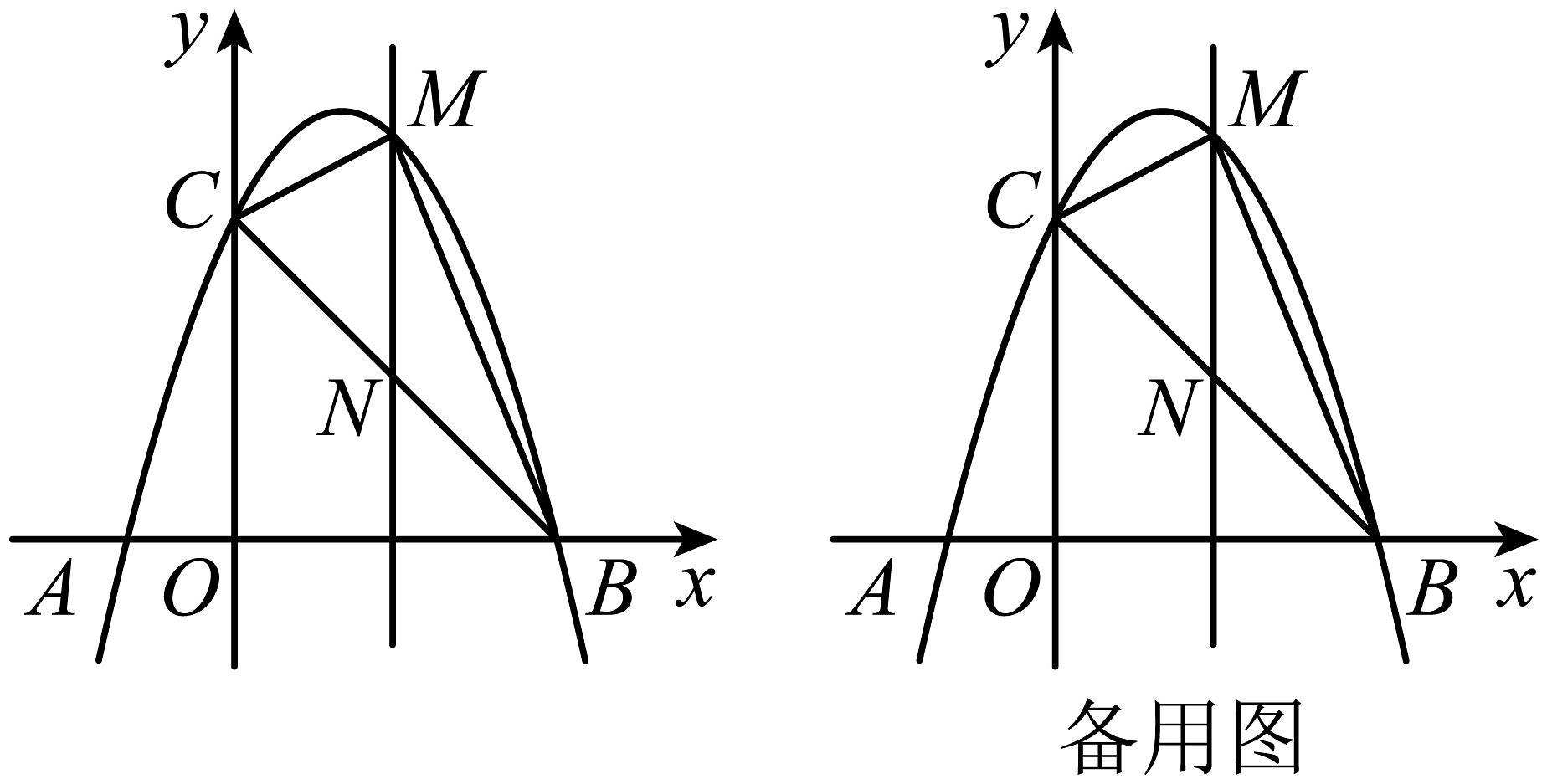 (1)、求抛物线的表达式;(2)、求线段的最大值;(3)、是否存在以为腰的等腰三角形?若存在,求出的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、求线段的最大值;(3)、是否存在以为腰的等腰三角形?若存在,求出的值;若不存在,请说明理由. -
20、如图,是的外接圆,为直径,点是劣弧的中点,连接 , , 过点作交的延长线于点 , 使得 .
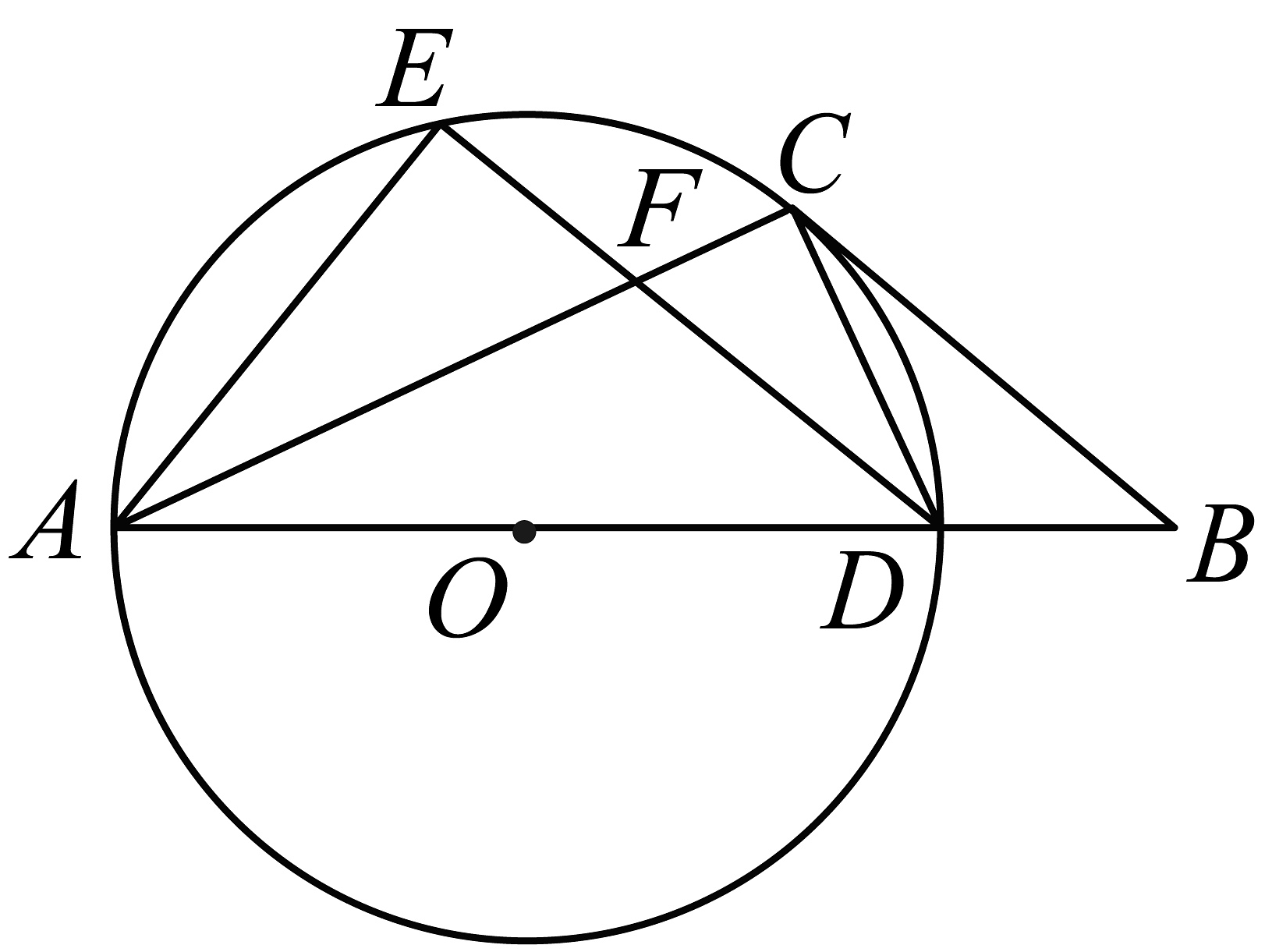 (1)、求证:为的切线;(2)、求证:;(3)、若的半径 , , 求的长度.
(1)、求证:为的切线;(2)、求证:;(3)、若的半径 , , 求的长度.