-
1、如图,这是U型磁铁示意图,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
2、在平面直角坐标系中,抛物线()的图象与x轴交于、两点,与y轴交于点 .
 (1)、求抛物线的解析式;(2)、如图1,点是直线上方抛物线上的一个动点,连接、;点为轴上的一个动点,点为轴上的一个动点,连接、、 . 当的面积取得最大值时,求点的坐标及周长的最小值;(3)、如图2,在(2)的条件下,连接 , 将抛物线沿射线的方向平移得到新抛物线 , 使得新抛物线经过点 , 且与直线相交于另一点 , 点为抛物线上的一个动点,当时,直接写出符合条件的所有点的坐标.
(1)、求抛物线的解析式;(2)、如图1,点是直线上方抛物线上的一个动点,连接、;点为轴上的一个动点,点为轴上的一个动点,连接、、 . 当的面积取得最大值时,求点的坐标及周长的最小值;(3)、如图2,在(2)的条件下,连接 , 将抛物线沿射线的方向平移得到新抛物线 , 使得新抛物线经过点 , 且与直线相交于另一点 , 点为抛物线上的一个动点,当时,直接写出符合条件的所有点的坐标. -
3、如图,是的切线,A为切点,是的弦,过O作于点H.若 , , . 求:
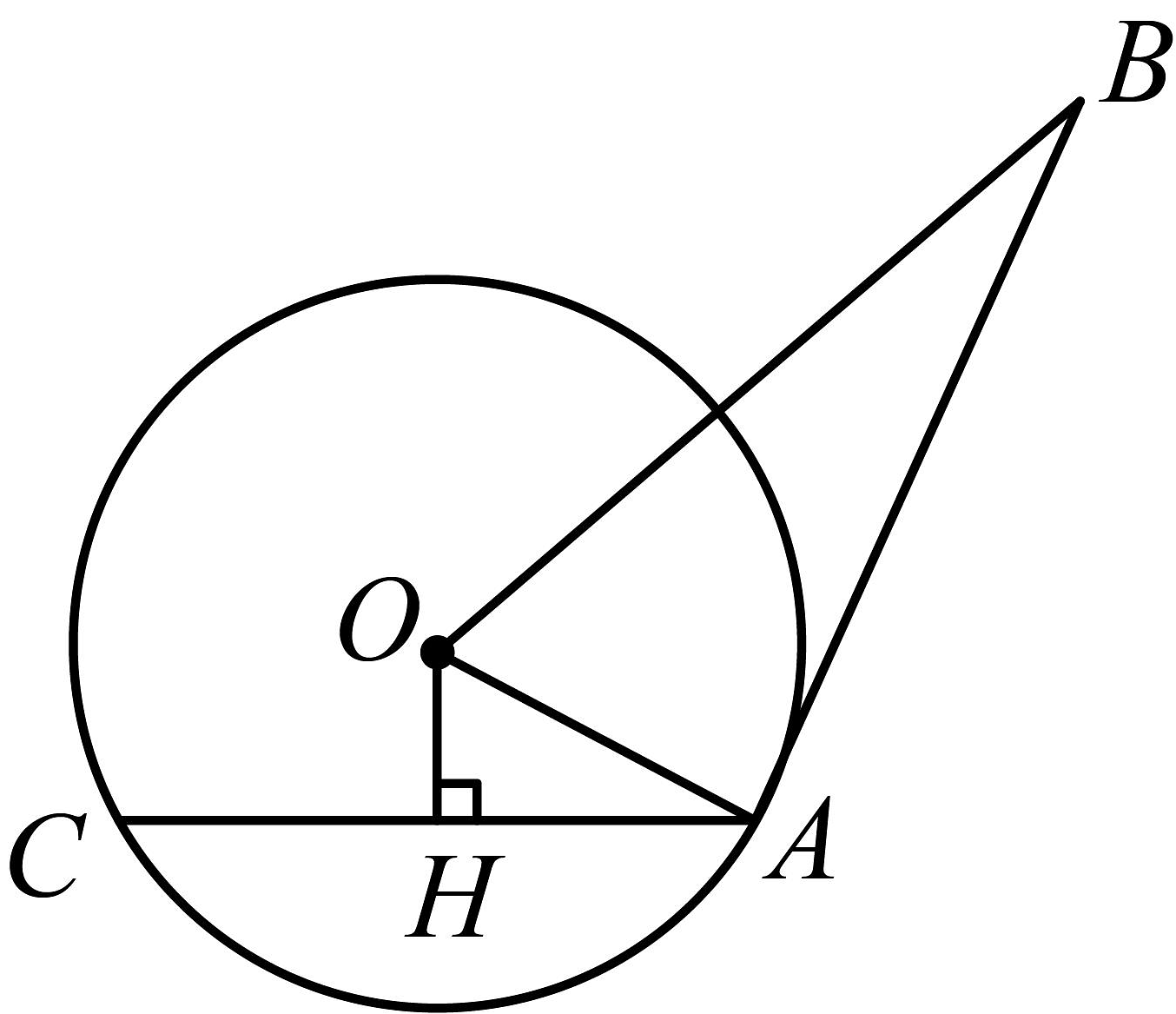 (1)、的半径;(2)、的值;
(1)、的半径;(2)、的值; -
4、如图,是的直径,为上一点,延长到点 , 过点作切于点 , 连接 , , 于点 , 交于点 , 交于点 .
 (1)、求证:;(2)、若 , , , 求的长.
(1)、求证:;(2)、若 , , , 求的长. -
5、如图,一次函数的图象与反比例函数的图象相交于两点,与轴交于点 .
 (1)、求一次函数的解析式;(2)、设为线段上的一个动点(不包括两点),过点作轴交反比例函数图象于点 , 当的面积是3时,求点的坐标.
(1)、求一次函数的解析式;(2)、设为线段上的一个动点(不包括两点),过点作轴交反比例函数图象于点 , 当的面积是3时,求点的坐标. -
6、某商场销售一批名牌衬衫,平均每天可销售件,每件盈利元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价元,商场平均每天可多售出件.求:(1)、若商场每件衬衫降价元,则商场每天可盈利多少元?(2)、若商场平均每天要盈利元,每件衬衫应降价多少元?
-
7、(1)计算: .
(2)解不等式: .
-
8、如图,在平面直角坐标系中,已知点 .
 (1)、作出关于原点O对称的;(2)、作出绕原点O顺时针旋转得到的 , 并写出点的坐标.
(1)、作出关于原点O对称的;(2)、作出绕原点O顺时针旋转得到的 , 并写出点的坐标. -
9、如图,在中, , 点在上,已知 , . 则 .

-
10、如图,在正方形中,为CD上一点,连接 , 过点作于点 , 若 , , 则 .

-
11、如图,是反比例函数图象上任意一点,过点作轴的垂线,垂足为 , 则的面积为 .

-
12、从这五个数中任选一个数,选出的这个数是无理数的概率是 .
-
13、如图,是的弦,半径于点C,为直径, , , 则线段的长为 .

-
14、二次函数的图象如图所示,若关于的一元二次方程有两个不相等的实数根,则整数的最小值为 .

-
15、一元二次方程的常数项是 .
-
16、如图,是的外接圆,P是延长线上一点,连接 , 且 , 点D是中点,的延长线交于点Q,则下列结论:①;②垂直平分;③直线和都是的切线;④ . 其中正确的结论是( )
 A、①④ B、②③ C、①②③ D、①②③④
A、①④ B、②③ C、①②③ D、①②③④ -
17、如图,是一个由4个相同的正方体组成的立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
18、如图,在中, , , , 点、 分别是、 上的动点,当 时,的最小值是( )
 A、8 B、 C、 D、9
A、8 B、 C、 D、9 -
19、由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.过点作的垂线交小正方形对角线的延长线于点 , 连结 , 延长交于点 . 若 , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、已知反比例函数 , 则下列点中在这个反比例函数图象上的是( )A、 B、 C、 D、