相关试卷

1、计算：

(1)、 $\sqrt{48} - 2 \sqrt{\frac{1}{2}} + \sqrt{3}$

(2)、 ${(2 \sqrt{3} - 1)}^{2} - (\sqrt{3} + 2) (\sqrt{3} - 2)$

查看解析
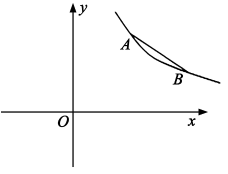
2、如图，已知点 $A (m ， m + 1) ， B (m + 3 ， m - 1)$ 都在反比例函数 $y = \frac{k_{1}}{x} (x > 0)$ 的图象上．将线段AB沿直线 $y = k_{2} x + b$ 进行对折得到线段 $A_{1} B_{1}$ ，且点 $A_{1}$ 始终在直线OA上．当线段 $A_{1} B_{1}$ 与x轴有交点时，b的取值的最大值是．

查看解析
3、如图，在矩形 $A B C D$ 中， $A B = 10$ ， $B C = 12$ ，点E在边 $A D$ 上，连接 $B E$ ，将 $△ A B E$ 沿 $B E$ 翻折，点A对应点为点F ，当直线 $B F$ 恰好经过 $C D$ 的中点M时， $A E$ 的长为．

查看解析
4、如图，在菱形 $A B C D$ 中，点P是对角线 $B D$ 上一动点， $P E ⊥ B C$ 于点E ， $P F ⊥ C D$ 于点F ，记菱形高线的长为h ，则下列结论：①当P为 $B D$ 中点时，则 $P E = P F$ ；② $P E + P F = h$ ；③ $∠ E P F + ∠ A = 180 °$ ；④若 $A B = 2, ∠ E P F = 60 °$ ，连接 $P C$ ，则 $P E + P C$ 有最小值为2；⑤若 $h = 2, ∠ E P F = 60 °$ ，连接 $E F$ ，则 $S_{△ P E F}$ 的最大值为 $\frac{\sqrt{3}}{2}$ ．其中错误的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看解析
5、如图，将含 $30 °$ 的三角尺放在平面直角坐标系 $x o y$ 中，点 $B$ 在 $x$ 轴上， $A C ∥ x$ 轴，点M为斜边AB的中点．若反比例函数 $y = \frac{m}{x}$ （ $m > 0$ ）的图象经过 $A, M$ 两点，反比例函数 $y = \frac{n}{x}$ （ $n > 0$ ）的图象经过点 $C$ ，则 $m$ 与 $n$ 满足的等量关系是（）

A、 $n = 3 m$ B、 $n = 2 m$ C、 $n = \sqrt{3} m$ D、 $n - m = \sqrt{3}$

查看解析
6、如图，点 $P$ 是矩形 $A B C D$ 的对角线 $A C$ 上一点，过点 $P$ 作 $E F ∥ B C$ ，分别交 $A B$ ， $C D$ 于 $E$ ， $F$ ，连接 $P B$ ， $P D$ ．若 $A E = 2$ ， $P F = 8$ ，则图中阴影部分的面积为（）

A、 $10$ B、 $12$ C、 $16$ D、 $18$

查看解析
7、已知点 $(- 2, y_{1})$ ， $(- 1, y_{2})$ ， $(3, y_{3})$ 都在反比例函数 $y = \frac{| k | + 1}{x}$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{2} < y_{3} < y_{1}$

查看解析
8、在 $△ A B C$ 中， $∠ C = R t ∠$ ，用反证法证明“在直角三角形中，至少有一个锐角不大于 $45 °$ ． ”的命题时，应先假设（）

A、 $∠ A$ ， $∠ B$ 都大于 $45 °$ B、 $∠ A$ ， $∠ B$ 都大于等于 $45 °$ C、 $∠ A$ ， $∠ B$ 都小于 $45 °$ D、 $∠ A$ ， $∠ B$ 都小于等于 $45 °$

查看解析
9、三角形的三条中位线的长分别为 $3 c m$ ， $4 c m$ ， $5 c m$ ，则原三角形的周长为（）

A、 $6.5 c m$ B、 $24 c m$ C、 $26 c m$ D、 $52 c m$

查看解析
10、如图所示，在 $⊙ O$ 中， $\overset{⌢}{A D} =$ $\overset{⌢}{A C}$ ，弦 $A B$ 与弦 $A C$ 交于点 $A$ ，弦 $C D$ 与 $A B$ 交于点 $F$ ，连接 $B C$ ．

(1)、求证： $A C^{2} = A B \cdot A F$ ；

(2)、若 $⊙ O$ 的直径长为 $8 cm$ ， $∠ B = 60 °$ ，求图中阴影部分面积．

查看解析
11、深圳地铁线路延长段工程正在紧锣密鼓施工，原计划40天完成一段轨道铺设任务．由于采用了新的施工技术，实际只用了25天就全部完工，并且实际每天铺设的轨道长度比原计划多150米．

(1)、求原计划每天铺设轨道多少米．

(2)、该地铁线路某站点的装修设计图中，要在一块矩形的墙面区域内，嵌入两个相同的正方形装饰图案．已知矩形墙面的长为8米，宽为6米，嵌入装饰图案后剩余可利用的墙面面积是原来矩形墙面面积的 $\frac{3}{4}$ ．求正方形装饰图案的边长为多少米．

查看解析
12、计算： $|- 3| - \frac{1}{2} \sqrt{12} + 4 cos 30 ° - {(π - 2025)}^{0}$ ．

查看解析
13、如图， $A O = B O = 50 cm ， O C$ 是一条射线， $O C ⊥ A B$ ，一只蚂蚁由点 $A$ 以 $2 cm / s$ 的速度向点 $B$ 爬行，同时另一只蚂蚁由点 $O$ 以 $3 cm / s$ 的速度沿 $O C$ 方向爬行，则经过 $s$ 后，两只蚂蚁与点 $O$ 组成的三角形的面积为 $450 {cm}^{2}$ ．

查看解析
14、如图，在平面直角坐标系中，一次函数 $y = - x + 1$ 与两坐标轴分别交于 $A$ ， $B$ 两点， $C$ 为线段 $A B$ 的中点，点 $P$ 在反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象上，则 $C P$ 的最小值为．

查看解析
15、一个锐角是 $21 ° 20^{'} 24^{"}$ ，它的余角是度．

查看解析
16、已知方程 $x^{2} - 17 x + 60 = 0$ 的两根恰好是 $Rt △ A B C$ 的两条边的长，则 $Rt △ A B C$ 的第三边长为．

查看解析
17、下列说法正确的是（）

A、可能性是 $99.9 %$ 的事件在一次实验中一定会发生 B、将只有颜色不同的5个白球、4个黑球放在一个不透明的布袋中，摸到白球和黑球的可能性相等 C、了解茅洲河的水质情况，采用抽样调查的方式 D、从4000名学生中随机抽取400名学生进行调查，样本容量为4000

查看解析
18、下列各数中，负数的是（）

A、 $|- 5|$ B、 $+ (- 4)$ C、0 D、 $- (- 3)$

查看解析
19、已知y与 $x - 1$ 成正比例，且当 $x = 3$ 时， $y = 4$ ．

(1)、求y与x之间的函数解析式；

(2)、当 $x = - 6$ 时，求y的值．

查看解析
20、如图，已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于 $A (1, 0)$ ， $B (4, 0)$ 两点，与y轴交于点C，点D为抛物线的顶点．

(1)、求抛物线的函数表达式及点D的坐标；

(2)、若四边形 $B C E F$ 为矩形， $C E = 3$ ．点M以每秒1个单位的速度从点C沿 $C E$ 向点E运动，同时点N以每秒2个单位的速度从点E沿 $E F$ 向点F运动，一点到达终点，另一点随之停止．当以M、E、N为顶点的三角形与 $△ B O C$ 相似时，求运动时间t的值；

(3)、抛物线的对称轴与x轴交于点P，点G是点P关于点D的对称点，点Q是x轴下方抛物线上的动点．若过点Q的直线 $l : y = k x + m (| k | < \frac{9}{4})$ 与抛物线只有一个公共点，且分别与线段 $G A$ 、 $G B$ 相交于点H、K，求证： $G H + G K$ 为定值．

查看解析

上一页 940 941 942 943 944 下一页跳转