-
1、已知关于的一元二次方程 .(1)、求证:无论取何值,此方程总有两个不相等的实数根.(2)、当方程的一个根是1时,求的值.
-
2、(1)、计算: .(2)、解方程: .
-
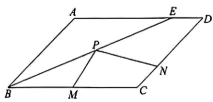
3、如图,在平行四边形中, , , 作的平分线交边于点 , 且有 , 是边上的动点,且满足 , 是边上的动点,连接 . 当时,的值为 .
-
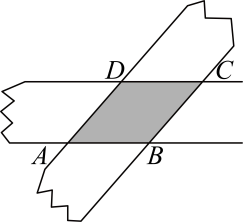
4、如图,两张等宽的纸条交叉叠放在一起,重合部分构成四边形 . 若测得 , 之间的距离为之间的距离为 , 则线段的长为 .
-
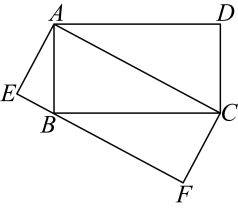
5、如图, , 都是矩形,而且点在边上,其中 , , 则矩形的面积为 .
-
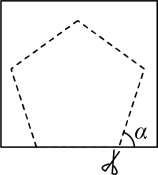
6、在剪纸活动中,小花同学想用一张长方形纸片剪出一个正五边形,其中正五边形的一条边与长方形的边重合,如图所示,则的大小是度.
-
7、方程的两根为 , , 则的值为 .
-
8、如图,把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形.如果图2中小正方形的边长为 , 图3中小正方形的边长为1,则图1中菱形的面积为( )
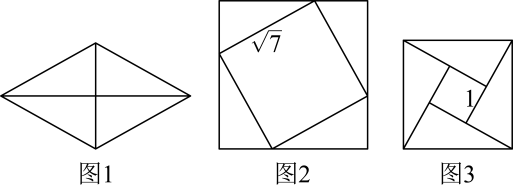 A、6 B、3 C、 D、12
A、6 B、3 C、 D、12 -
9、已知平面直角坐标系中有四个点,其中点 , 若以为顶点的四边形是平行四边形,则点的坐标可以是( )A、 B、 C、 D、
-
10、如图是脊柱侧弯的检测示意图,在体检时为方便测出角的大小,需将转化为与它相等的角,则图中与相等的角是( )
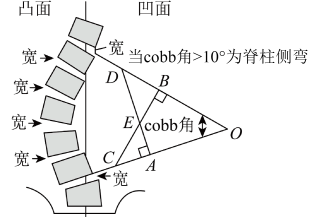 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,用一根绳子检测一个平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量两条对角线就可以判断了.这种检测方法用到的数学依据是( )
 A、两条对角线互相平分的平行四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的平行四边形是矩形 D、对角线平分每组对角的平行四边形是矩形
A、两条对角线互相平分的平行四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的平行四边形是矩形 D、对角线平分每组对角的平行四边形是矩形 -
12、用反证法证明命题:“已知△ABC , AB=AC;求证:∠B90°.”第一步应先假设( )A、 B、 C、 D、
-
13、一组数据:2,3,4,6,6,5,这组数据的中位数、众数分别是( )A、3,6 B、5,3 C、3.5,6 D、4.5,6
-
14、用配方法解一元二次方程 , 变形后的结果正确的是( )A、 B、 C、 D、
-
15、下列式子是最简二次根式的是( )A、 B、 C、 D、
-
16、如图1,点分别在直线和上, , 射线从射线的位置开始,绕点以每秒的速度逆时针旋转,同时射线从射线的位置开始,绕点以每秒的速度逆时针旋转,射线旋转到的位置时,两者停止运动.设旋转时间为秒.
 (1)、①的度数为 ▲ (用的代数式表示);
(1)、①的度数为 ▲ (用的代数式表示);②当射线经过点时,此时的度数为 ▲ .
(2)、在转动过程中,是否存在某个时刻,使得射线与射线所在直线的夹角为?若存在,求出的值;若不存在,请说明理由.(3)、在转动过程中,若射线与射线交于点 , 过点作交直线于点 , 与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由. -
17、根据以下素材,探索完成任务.
如何合理搭配消费券?
素材一
某市在今年发放了如图所示的超市购物消费券,规定每人可领取一套消费券(共5张):包含型消费券(满50减20元)2张,型消费券(满100减30元)2张,型消费券(满300减100元)1张.

素材二
在此次活动中,小明一家4人各领到了一套消费券.某日小明一家在超市使用消费券共减了480元.
解决问题
任务一
若小明一家用了2张型消费券,2张型消费券,则用了 ▲ 张型消费券,此时实际消费最少为 ▲ 元.
任务二
若小明一家此次消费共用了11张消费券,其中型比型的消费券多4张,求型的消费券各用了多少张.
任务三
若小明一家仅用两种不同类型的消费券组合消费,请问该如何使用消费券,才能使得实际消费金额最小,并求出此时的实际最小消费金额.
-
18、如图,在正方形中放入两张边长分别为和的正方形纸片,已知 , 正方形的面积记为 , 阴影部分面积分别记为 , .
 (1)、用含 , , 的代数式分别表示 , ;(2)、若 , 且 , 求的值;(3)、若 , 试说明的完全平方式.
(1)、用含 , , 的代数式分别表示 , ;(2)、若 , 且 , 求的值;(3)、若 , 试说明的完全平方式. -
19、(1)、已知 , , 求代数式的值.(2)、已知 , 求代数式的值.
-
20、先化简 , 再从1, , 2,中选择一个合适的x值代入求代数式的值.