-
1、关于一次函数 , 下列说法正确的是( )A、图象经过第二,三,四象限 B、图象与轴交于点 C、图象向下平移6个单位经过原点 D、点在函数图象上
-
2、在中, , , 的对边分别记为a , b , c , 下列条件不能够判定为直角三角形的是( )A、 B、 C、 , , D、
-
3、下列说法正确的是( )A、是最简二次根式 B、 C、 D、与可以合并
-
4、如图1,反比例函数与一次函数的图象交于点 , 点 , 一次函数与轴相交于点 .
 (1)、求反比例函数和一次函数的表达式;(2)、连接 , , 求的面积;(3)、如图2,点是反比例函数图象上点右侧一点,连接 , 把线段绕点顺时针旋转 , 点的对应点恰好也落在这个反比例函数的图象上,求点的坐标.
(1)、求反比例函数和一次函数的表达式;(2)、连接 , , 求的面积;(3)、如图2,点是反比例函数图象上点右侧一点,连接 , 把线段绕点顺时针旋转 , 点的对应点恰好也落在这个反比例函数的图象上,求点的坐标. -
5、如图,在▱中, , 点是的中点,连结并延长,交的延长线于点 , 连结 , .
 (1)、求的长;(2)、若 .
(1)、求的长;(2)、若 .①证明四边形是菱形;
②若 , 求四边形的周长.
-
6、2023年第19届亚运会将在杭州举行,某校举办了“迎亚运,展风采”知识竞赛,学生得分均为整数,为了解学生对亚运知识的掌握情况,结果如下:
七年级10名学生的竞赛成绩:94,83,94,85,96,94,88,95,87,84.
八年级10名学生的竞赛成绩:83,95,86,84,95,82,89,95,91,100
对上述两个年级各10名学生的竞赛成绩做如下分析:
年级
平均数
众数
中位数
方差
七年级
90
b
91
d
八年级
a
95
c
34.2
根据以上信息,解答下列问题:
(1)、请直接写出a , b , c , d的值.(2)、你认为上述七、八年级各10名学生的竞赛成绩哪个年级好?为什么?(3)、圆圆说:“由样本数据可以估计本次竞赛七年级学生中肯定没有同学得满分”.你认为圆圆的说法正确吗?请说明理由. -
7、如图,在6×6网格中,每个小正方形的边长都是1,每个顶点称为格点.
线段AB的端点都在格点上.按下列要求作图,使所画图形的顶点均在格点上.
 (1)、如图1,画一个以AB为边的平行四边形.(2)、如图2,画一个以AB为边,且面积为12的平行四边形.(3)、如图3,画一个以AB为对角线,且面积为7的平行四边形.
(1)、如图1,画一个以AB为边的平行四边形.(2)、如图2,画一个以AB为边,且面积为12的平行四边形.(3)、如图3,画一个以AB为对角线,且面积为7的平行四边形. -
8、解下列方程:(1)、(2)、2x2-5x+2=0
-
9、计算:(1)、(2)、
-
10、如图,在菱形ABCD中,点P是对角线BD上一动点,PE⊥BC于点E , PF⊥CD于点F , 记菱形高线的长为h , 则下列结论:
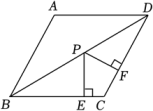
①当P为BD中点时,则PE=PF;②PE+PF=h;
③∠EPF+∠A=180°;④若AB=2,∠EPF=60°,连结PC , 则PE+PC有最小值为2;
⑤若h=2,∠EPF=60°,连结EF , 则S△PEF的最大值为 .
其中正确的结论有(填序号).
-
11、 如图,△OAC和△BAD都是等腰直角三角形, , 反比例函数在第一象限的图象经过点 , 则△OAC与△BAD的面积之差为 .

-
12、反比例函数 , 其中 . 若点均在该函数的图象上,则( )A、 B、 C、 D、
-
13、如图,菱形中,点 , 点 , 与交于点 , 反比例函数的图象经过点 , 则值为( )
 A、 B、—2 C、 D、2
A、 B、—2 C、 D、2 -
14、把一个长方形的纸片按如甲乙图形对折两次,然后剪下图丙中的①部分,为了得到一个锐角为30°的菱形,剪口与折痕所成的角的度数应为( )
 A、60°或30° B、30°或45° C、45°或60° D、75°或15°
A、60°或30° B、30°或45° C、45°或60° D、75°或15° -
15、方程(x-2)2=4(x-2)( )A、4 B、-2 C、4或-6 D、6或2
-
16、如图1,直线 , 且 . 点在直线上.点在直线上,动点从点出发,以每秒的速度向点运动,同时动点以同样的速度从点出发,向点运动.点运动的时间为 .
 (1)、当为何值时,四边形为平行四边形?并判断此时四边形的面积与四边形的面积有什么关系.(2)、是否存在的值,使四边形为菱形?若存在,求出的值;若不存在,说明理由.并探究如何只改变点的速度(匀速运动),使四边形在某一时刻为菱形,求点的速度.(3)、如图2,在(2)的条件下,将菱形绕点逆时针旋转得到菱形与直线相交于点 , 求四边形的面积.
(1)、当为何值时,四边形为平行四边形?并判断此时四边形的面积与四边形的面积有什么关系.(2)、是否存在的值,使四边形为菱形?若存在,求出的值;若不存在,说明理由.并探究如何只改变点的速度(匀速运动),使四边形在某一时刻为菱形,求点的速度.(3)、如图2,在(2)的条件下,将菱形绕点逆时针旋转得到菱形与直线相交于点 , 求四边形的面积. -
17、山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一,其中“蔡岭”在2019年“五一”小长假期间,接待游客达2万人次,预计在2021年“五一”小长假期间,接待游客2.88万人次,在蔡岭,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗10元,借鉴以往经验,若每碗卖15元,平均每天将销售120碗,若价格每提高0.5元,则平均每天少销售4碗,每天店面所需其他各种费用为168元.(1)、求出2019至2021年“五一”小长假期间游客人次的年平均增长率;(2)、为了更好地维护东至县形象,物价局规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天净利润600元?(净利润=总收入﹣总成本﹣其它各种费用)
-
18、为了解学生关注热点新闻的情况,“两会”期间,小帅对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
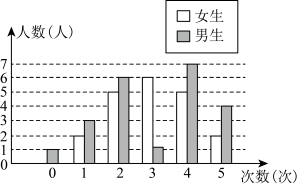 (1)、该班级的女生人数是 , 女生收看“两会”新闻次数的中位数是 .(2)、对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低 , 试求该班级的男生人数.(3)、为进一步分析该班级男、女生收看“两会”新闻次数的特点,小帅给出了部分统计量(如表).
(1)、该班级的女生人数是 , 女生收看“两会”新闻次数的中位数是 .(2)、对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低 , 试求该班级的男生人数.(3)、为进一步分析该班级男、女生收看“两会”新闻次数的特点,小帅给出了部分统计量(如表).统计量
平均数(次)
方差(次)
. ..
女生
3
1.3
. ..
男生
3
2
. ..
根据你学过的统计知识,比较该班级男、女生收看“两会”新闻次数的波动情况.
-
19、已知:如图,是正方形的边上的两点, , 连接 .
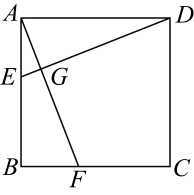 (1)、求证: .(2)、求的度数.
(1)、求证: .(2)、求的度数. -
20、如图1,已知 , 用直尺和圆规作以为邻边的平行四边形 .
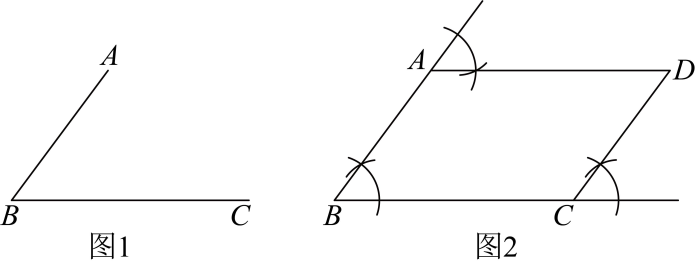 (1)、如图2,根据作图痕迹,证明四边形为平行四边形.(2)、在图1中,请你再作一个平行四边形(方法与上题不一样,保留作图痕迹,不需要证明).
(1)、如图2,根据作图痕迹,证明四边形为平行四边形.(2)、在图1中,请你再作一个平行四边形(方法与上题不一样,保留作图痕迹,不需要证明).