相关试卷

1、随着经济复苏，某公司近两年的总收入逐年递增，该公司2021年缴税40万，2023年缴税48.4万，该公司这两年缴税的年平均增长率是（）

A、 $10 %$ B、 $15 %$ C、 $20 %$ D、 $25 %$

查看解析
2、二次函数 $y = 2 (x + 1)^{2} - 7$ 的最小值是（）

A、 $- 7$ B、1 C、 $- 1$ D、7

查看解析
3、三个大小相同的正方体搭成的几何体如图所示，其俯视图是（）

A、 B、 C、 D、

查看解析
4、将20109用科学记数法表示为（）

A、 $2.0109 \times 1 0^{4}$ B、 $20.109 \times 1 0^{3}$ C、 $201.09 \times 1 0^{2}$ D、 $0.20109 \times 1 0^{5}$

查看解析
5、剪纸是我国最古老的民间艺术之一．下列剪纸图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
6、 $\frac{5}{2}$ 的相反数为（）

A、 $- 2.5$ B、 $2.5$ C、 $- \frac{2}{5}$ D、 $\frac{2}{5}$

查看解析
7、如图，已知 $A F$ 是 $⊙ O$ 的直径，弦 $B C ⊥ A F$ 于点 $G$ ， $D$ 是弧 $A C$ 上的一点， $A D$ ， $B C$ 的延长线交于点 $E$ ．连接 $B D$ 交 $A F$ 于点 $M$ ．连结 $C D$ ，若 $E D = 2 A D$ ．

(1)、【认识图形】求证： $∠ E D C = ∠ A D B$

(2)、【探索关系】① $B D$ 与 $B E$ 之间有什么数量关系？
②设 $\frac{D M}{M B} = x$ ， $\frac{G E}{B G} = y$ ，求 $y$ 关于 $x$ 的函数关系式．

(3)、【问题解决】若 $B M = 3 \sqrt{3}$ ， $M D = 4 \sqrt{3}$ ，求 $A D$ 的长．

查看解析
8、二次函数 $y = x^{2} - 2 m x (m \neq 0)$ 的图象经过点 $A (2 m + 1, y_{1})$ ，点 $B (m - 1, y_{2})$ ．

(1)、若 $m = 2$ ，求抛物线的顶点坐标；

(2)、若存在实数 $k$ ，使得 $y_{2} - 1 = k (y_{1} - 1)$ ，且 $1 < k < 2$ ，求 $m$ 的取值范围；

(3)、当 $m - 1 \leq x \leq 2 m + 1$ 时，随着 $x$ 增大， $y$ 先减小再增大， $y$ 的最大值与 $y$ 的最小值的和为 $\frac{1}{2}$ ，求 $m$ 的值．

查看解析
9、如图1，直线 $y = k x + 1 (k > 0)$ 分别与x轴，y轴相交于A ， B两点，直线 $y = \frac{3}{4} x - 3$ 分别与x轴，y轴相交于C ， D两点，两条直线相交于点E ．

(1)、点C的坐标为，点A的坐标为（点A用含k的代数式表示）．

(2)、若点A关于y轴的对称点 $A^{'}$ 恰好落在 $△ B D E$ 的内部，求k的取值范围．

(3)、如图2，若点D为 $C E$ 的中点，点Q为直线 $A B$ 上一点，连接 $D Q$ ，记点E关于直线 $D Q$ 的对称点为 $E^{'}$ ．请问：是否存在点Q ，使得点 $E^{'}$ 恰好落在直线 $C D$ 上方的坐标轴上？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看解析
10、已知：如图，在四边形 $A B C D$ 中， $A B = C D ， E ， F ， G$ 分别是 $A D ， B C ， B D$ 的中点，可证： $∠ G E F = ∠ G F E$ （无需证明）．
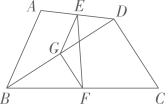
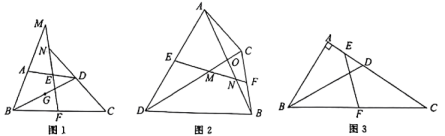
拓展：

(1)、如图1；在四边形 $A B C D$ 中， $A B = C D ， E ， F ， G$ 分别是 $A D ， B C ， B D$ 的中点，分别延长 $B A ， F E ， C D$ ，交于 $M ， N$ 两点，求证： $∠ M = ∠ C N F$ ．

(2)、如图2，在四边形 $A D B C$ 中， $A B$ 与 $C D$ 相交于点 $O ， A B = C D ， E ， F$ 分别是 $A D ， B C$ 的中点，连结 $E F$ ，分别交 $D C$ ， $A B$ 于点 $M$ ， $N$ ，判断 $△ O M N$ 的形状：（直接写出答案，无需证明）．

(3)、如图3，在 $△ A B C$ 中， $∠ A = 90 °$ ， $D$ 是 $A C$ 上一点，且 $C D = A B = 10$ ， $E$ ， $F$ 分别是 $A D$ ， $B C$ 的中点，求 $E F$ 的长．

查看解析
11、为了解某校九年级学生的一分钟跳绳情况，随机抽取了部分学生进行调查，并将跳绳个数分为五组： $A . 175 \sim 195$ ， $B . 155 \sim 175$ ， $C . 135 \sim 155$ ， $D . 115 \sim 135$ ， $E . 95 \sim 115$ ．（每组含后一个边界值，不含前一个边界值），绘制成如下两幅不完整的统计图.请根据信息，解答下列问题：

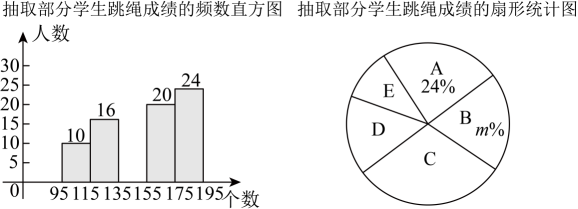(1)、扇形统计图中的 $m =$ ， $E$ 组所对圆心角度数为．

(2)、补全条形统计图．

(3)、已知该校共有九年级学生450人，已知一分钟跳绳个数超过175个为满分，请估计该校九年级学生一分钟跳绳的满分人数。

查看解析
12、如图，在 $△ A B C$ 中， $A D ⊥ B C$ ， $∠ A C B$ 的平分线 $C E$ 交 $A D$ 于点 $F$ ， $A C = 10$ ， $s i n ∠ C A D = \frac{3}{5}$ ．

(1)、求 $A D$ 的长．

(2)、求 $c o s ∠ A C E$ 的值．

查看解析
13、解分式方程：

(1)、 $\frac{11 - 2 x}{4 - x} = \frac{1 - x}{x - 4}$ ；

(2)、 $\frac{3}{x} - \frac{6}{1 - x} = \frac{x + 5}{x (1 - x)}$ ．

查看解析
14、计算： $| - 2 | + {(\frac{1}{2})}^{- 2} - {(s i n 60 ° - 1)}^{0}$

查看解析
15、如图，在矩形 $A B C D$ 中，已知 $\frac{A B}{B C} = \frac{3}{5}$ ，点 $E$ 是对角线 $A C$ 上一动点，边 $A B$ 绕点 $E$ 按逆时针方向旋转 $90 °$ 得到线段 $M N$ ，连结 $B N$ ， $C M$ ．当点 $M$ 落在边 $B C$ 上时， $\frac{B N}{C M}$ 的值为．

查看解析
16、如图， $A, B, C$ 是在 $⊙ O$ 上的点， $∠ C = 30 °$ ， $O A = 2$ ，则 $\overset{⌢}{A B}$ 的长为．（结果保留 $π$ ）

查看解析
17、若m是方程 $2 x^{2} - 3 x + 1 = 0$ 的一个根，则 $4 m^{2} - 6 m + 2026$ 的值为．

查看解析
18、已知 $△ A_{1} B_{1} C_{1}, △ A_{2} B_{2} C_{2}$ 的面积相等，现有两个判断：①若 $A_{1} B_{1} = A_{2} B_{2}, A_{1} C_{1} = A_{2} C_{2}$ ，则 $△ A_{1} B_{1} C_{1} ≌ △ A_{2} B_{2} C_{2}$ ；②若 $∠ A_{1} = ∠ A_{2}, ∠ B_{1} = ∠ B_{2}$ ，则 $△ A_{1} B_{1} C_{1} ≌ △ A_{2} B_{2} C_{2}$ ．对于上述的两个判断，下列说法正确的是（）

A、①正确，②错误 B、①错误，②正确 C、①②都错误 D、①②都正确

查看解析
19、清代数学家梅文鼎在《几何通解》中指出：若一直角三角形的股长是勾长的二倍，则这个直角三角形的勾弦之和等于勾弦之差再加上股，其勾弦之和就被勾弦之差和股分成中末比（即黄金分割比 $\frac{\sqrt{5} - 1}{2}$ ）．如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 4 ， B C = 2$ ．点 $D$ 在边 $A B$ 上，过点 $D$ 作 $D E ⊥ A C$ 于点 $E$ ，作 $D F$ $⊥ B C$ 于点 $F$ ，若四边形 $D E C F$ 的周长与 $R t △ A B C$ 的周长之比恰好为中末比，则 $A D$ 的长为（）

A、 $3 \sqrt{5} - 5$ B、 $3 - \sqrt{5}$ C、 $6 - 3 \sqrt{5}$ D、 $5 - \sqrt{5}$

查看解析
20、下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(x y)}^{4} = x y^{4}$ C、 ${(x^{2})}^{3} = x^{6}$ D、 $x^{6} \div x^{3} = x^{2}$

查看解析

上一页 935 936 937 938 939 下一页跳转