-
1、在古代数学名著里,记载了利用算筹实施“正负术”的方法.图1表示计算的过程,按照这种方法,图2的计算过程表示的算式为( )
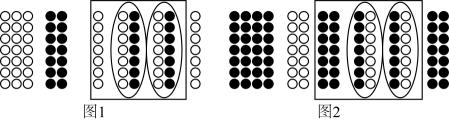 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图1所示的云梯是古代攻城用的器械,传说由鲁班发明.云梯底架以木为床,下置六轮,梯身以一定角度固定装置于底盘上,并在主梯之外增设了一具可以活动的副梯,主、副梯长度相等,立柱、底板、主梯构成一个三角形.如图2为其平面示意图, , 米,AD可以绕点A旋转,以便调节云梯的高.
 (1)、若 , , 求的度数;(2)、当时,计算出点D到的距离.
(1)、若 , , 求的度数;(2)、当时,计算出点D到的距离. -
3、正方形是我们熟悉的几何图形,它有着非常多的性质.如图1,正方形的边长是4,是对角线上一点.
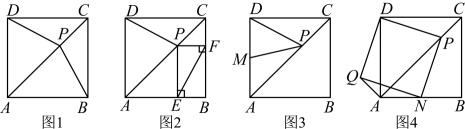 (1)、求证: .(2)、如图2,过点作 , , 垂足分别为 , , 连接 , 猜想与的数量关系,并证明你的猜想.(3)、如图3,是的中点,连接 , , 求的最小值.(4)、如图4,过点作 , 交于点 , 以 , 为邻边作矩形 , 连接 , 若恰好为的中点,直接写出矩形的面积.
(1)、求证: .(2)、如图2,过点作 , , 垂足分别为 , , 连接 , 猜想与的数量关系,并证明你的猜想.(3)、如图3,是的中点,连接 , , 求的最小值.(4)、如图4,过点作 , 交于点 , 以 , 为邻边作矩形 , 连接 , 若恰好为的中点,直接写出矩形的面积. -
4、已知:如图所示,在平面直角坐标系中,过点的直线与直线相交于点 , 与y轴交于点M .
 (1)、求直线的表达式.(2)、求的面积.(3)、若一次函数的图像为 , 且、、不能围成三角形,直接写出n的值.
(1)、求直线的表达式.(2)、求的面积.(3)、若一次函数的图像为 , 且、、不能围成三角形,直接写出n的值. -
5、某班40名学生进行数学测验(满分20分),随机抽取10人的真实成绩如下:16,18,15,12,20,17,18,14,18,19.(1)、直接写出该样本数据的中位数和众数;(2)、嘉嘉抄录样本数据时有一个成绩抄错,导致众数发生变化,则他抄错的原成绩是分;(3)、已知全班的平均分是16.2分.淇淇说:所抽取的这10名学生成绩与全班相比,平均水平更高.通过计算说明淇淇的说法是否正确.
-
6、如图,在平行四边形中,
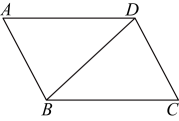 (1)、尺规作图:作对角线的中点(保留作图痕迹,不写作图过程);(2)、过点作直线分别交 , 于点 , ,
(1)、尺规作图:作对角线的中点(保留作图痕迹,不写作图过程);(2)、过点作直线分别交 , 于点 , ,①求证:;
②连接 , 若的外心在上,的周长为24,求平行四边形的周长.
-
7、计算:(1)、;(2)、 .
-
8、某商场销售一种儿童滑板车,经市场调查,售价(元/件)、每星期销量(件)之间的函数解析式为;售价(元/件)与单件利润(元)之间的关系如图所示.
 (1)、与之间的函数解析式为;(不必写范围)(2)、若某星期该滑板车单件利润为25元,则本星期该滑板车的销量为件.
(1)、与之间的函数解析式为;(不必写范围)(2)、若某星期该滑板车单件利润为25元,则本星期该滑板车的销量为件. -
9、已知等腰三角形周长为16,则底边长y关于腰长x的函数解析式为(x为自变量);自变量的取值范围;
-
10、如图,是跷跷板示意图,支柱经过的中点O , 与地面垂直于点M , , 当跷跷板的一端A着地时,另一端B离地面的高度为cm.

-
11、若一次函数上有两点和 , 则与的大小关系为(填“>“、“<“或“=“).
-
12、如图,在菱形中, , , 是上一点, , 是边上一动点,将四边形沿直线折叠,的对应点 . 当的长度最小时,则的长为( )
 A、7 B、6 C、5 D、6.5
A、7 B、6 C、5 D、6.5 -
13、在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为(0,3)、(t , 3)、(t , 0),点D是直线y=kx+1与y轴的交点,若点A关于直线y=kx+1的对称点恰好落在四边形OABC内部(不包括正好落在边上),则t的取值范围为( )
 A、-2<t<2 B、-2<t<2 C、-2<t<-2或2<t<2 D、以上答案都不对
A、-2<t<2 B、-2<t<2 C、-2<t<-2或2<t<2 D、以上答案都不对 -
14、小明想画出平行四边形 , 他的方法如下图:点B是的边上的一点,用无刻度的直尺和圆规作一条射线 , 接下来的画图小亮和小红分别给出建议.小亮:分别在射线和射线上截取 , 连接 , 四边形即为平行四边形;小红:在射线上截取线段 , 作 , 交射线于点C , 四边形即为平行四边形.下列说法正确的是( )
 A、小红的方法正确,小亮的方法不正确 B、小红的方法不正确,小亮的方法正确 C、小红、小亮的方法都正确 D、小红、小亮的方法都不正确
A、小红的方法正确,小亮的方法不正确 B、小红的方法不正确,小亮的方法正确 C、小红、小亮的方法都正确 D、小红、小亮的方法都不正确 -
15、如图,四边形是菱形, , , 于点 , 则的长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、如图,正方形 , , 的边长分别为直角三角形的三边长.若正方形 , 的边长分别为6和11,则正方形的面积为( )
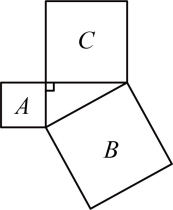 A、5 B、8 C、85 D、157
A、5 B、8 C、85 D、157 -
17、某校九(1)班全体43名学生身高的平均数与中位数都是 , 但后来发现其中有一位同学的身高登记错误,将登记成 , 经重新计算后,正确的平均数是 , 中位数是 , 则下列正确的是( )A、 B、 C、 D、
-
18、矩形、菱形都具有的性质是( )A、对角线相等 B、每一条对角线平分一组对角 C、对角线互相平分 D、对角线互相垂直
-
19、如图,在等腰中, , AD平分 , 点E为AC的中点,则DE的长等于( )
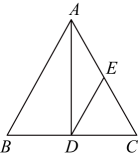 A、8 B、6 C、4 D、5
A、8 B、6 C、4 D、5 -
20、如图,在中,按照如下尺规作图的步骤进行操作:①以点B为圆心 , 以适当长为半径画弧,分别与交于点E、F;②分别以E、F为圆心,以适当长为半径画弧,两弧交于点G , 作射线 , 与边交于点H;③以B为圆心,长为半径画弧,交于边于点M . 若 , 则点A , M之间的距离为( )
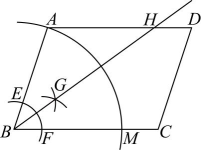 A、8 B、7 C、6 D、5
A、8 B、7 C、6 D、5