-
1、 如图,在等边三角形中,D为边上一点,E为边上一点,且 , 若 , 则的面积为 .

-
2、 某校运会百米预赛用抽签方式确定赛道,8条赛道的编号分别为1到8.若小张第一个抽签,她随机抽取一签,则抽到6号赛道的概率是 .
-
3、 计算:.
-
4、 如图,在等腰直角三角形中,是上一点, , 连接 , , 交的垂线于点 . 连接 , 交于 , 若设 , 在的运动过程中,下列代数式的值不变的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、 如图在平行四边形中,按以下步骤作图:①以点B为圆心,以适当长为半径作弧,分别交 , 于点M,N;②分别以M,N为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 交于点E,交延长线于点.若 , , 下列结论错误的是( )
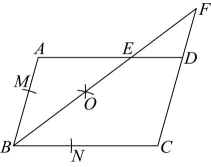 A、 B、 C、 D、
A、 B、 C、 D、 -
6、 《九章算术》中的算筹图是竖排的,现在改为横排,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表示出来,就是 , 在图2所示的算筹图中有一个图形被墨水覆盖了,若图2所表示的方程组中x的值为3,则被墨水所覆盖的图形为( )
 A、 B、 C、
A、 B、 C、 D、
D、
-
7、 如图,点A,B,C在上,垂直平分于点 . 现测得 , 则圆的半径为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 截止近日,电影《哪吒之魔童闹海》全球票房累计约达15400000000元,数据15400000000用科学记数法可表示为( )A、 B、 C、 D、
-
9、 如图表示某天我国城市的最低气温,这些城市中气温最高是( )
 A、武汉 B、广州 C、北京 D、哈尔滨
A、武汉 B、广州 C、北京 D、哈尔滨 -
10、已知 , 点B在直线之间, .
 (1)、如图1,请直接写出和之间的数量关系:_________.(2)、如图2,和满足怎样的数量关系?请说明理由.(3)、如图3,平分 , 平分 , 与交于点G,则的度数为_________.
(1)、如图1,请直接写出和之间的数量关系:_________.(2)、如图2,和满足怎样的数量关系?请说明理由.(3)、如图3,平分 , 平分 , 与交于点G,则的度数为_________. -
11、的三个顶点坐标分别为 , 将平移至的位置,点A、B、C对应的点分别为、、 , 已知点的坐标是(﹣2,3).
 (1)、求点、的坐标;(2)、在如图的平面直角坐标系中,画出和;(3)、已知内有一点 , 直接写出它在的对应点P的坐标.
(1)、求点、的坐标;(2)、在如图的平面直角坐标系中,画出和;(3)、已知内有一点 , 直接写出它在的对应点P的坐标. -
12、如图,已知 , 于D,于F.
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
13、已知某正数m的两个不同的平方根是和 , 求这个正数m的值.
-
14、解不等式: .
-
15、我国从2011年5月1日起在公众场所实行“禁烟”.为配合“禁烟”行动.某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对—题记10分.答错(或不答)一题记一5分.小明参加本次竞赛得分要超过100分.他至少要答对道题.
-
16、如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠EFC'=125°,那么∠AEB的度数是 .

-
17、“六•一”儿童节前夕,某超市用3360元购进A,B两种童装共120套,其中A型童装每套24元,B型童装每套36元.若设购买A型童装x套,B型童装y套,依题意列方程组正确的是( )A、 B、 C、 D、
-
18、已知是二元一次方程4x+ay=7的一组解,则a的值为( )A、 B、5 C、﹣5 D、﹣
-
19、
 (1)、【基础巩固】如图1,在矩形ABCD中,对角线AC、BD相交于点O,过点O的线段分别交AD、BC于点E、F,求证:OE=OF.(2)、【尝试运用】如图2,在矩形ABCD中,点O是对角线BD的中点,分别交AD、BC于点E、F,连结OE、OF,试猜想OE、OF的数量关系,并证明你的猜想.(3)、【拓展提高】如图3,在矩形ABCD中,点M,N是对角线BD的三等分点,过点M作分别交AD、BC于点E、F,连结EN、FN,已知 , , 求线段MF的长.
(1)、【基础巩固】如图1,在矩形ABCD中,对角线AC、BD相交于点O,过点O的线段分别交AD、BC于点E、F,求证:OE=OF.(2)、【尝试运用】如图2,在矩形ABCD中,点O是对角线BD的中点,分别交AD、BC于点E、F,连结OE、OF,试猜想OE、OF的数量关系,并证明你的猜想.(3)、【拓展提高】如图3,在矩形ABCD中,点M,N是对角线BD的三等分点,过点M作分别交AD、BC于点E、F,连结EN、FN,已知 , , 求线段MF的长. -
20、 一次函数 (k为常数),且 .(1)、 若点(-1,4)在一次函数的图象上,求一次函数的解析式.(2)、 当 时,一次函数 (k 为常数,且 )有最大值 k,求 k 的值.(3)、 若一次函数 (k 为常数,且 )与 x 轴的交点为(m,0),且 , 设 , 求 P 的取值范围.