-
1、下列几何体中,有一个几何体的主视图的形状与其它三个不一样,这个几何体是( )A、
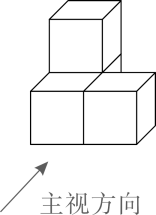 B、
B、 C、
C、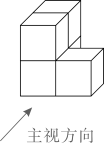 D、
D、
-
2、 如图1,点是正方形内部的一点, . 连接 , , 过点作的垂线交的延长线于点 .

 (1)、猜测的度数,并说明理由;(2)、若 , 求正方形的边长;(3)、如图2,过点作的垂线交于点 . 当恰好过的中点时,设正方形的边长为 , 用含的代数式表示 .
(1)、猜测的度数,并说明理由;(2)、若 , 求正方形的边长;(3)、如图2,过点作的垂线交于点 . 当恰好过的中点时,设正方形的边长为 , 用含的代数式表示 . -
3、 界首市公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月增长率;(2)、若此种头盔的进价为30元/个,经测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元,则月销售量将减少10个.
①为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?.
②要使销售该品牌头盔每月获得的利润最大,则该品牌头盔每个的售价为 ▲ 元?
-
4、 如图,菱形的对角线 , 相交于点O,E是的中点,点F,G在上, , .
 (1)、求证:四边形是矩形;(2)、若 , , 求的长.
(1)、求证:四边形是矩形;(2)、若 , , 求的长. -
5、 如图,在中, , 点E,F分别是的中点,
 (1)、尺规作图:作的平分线交于点D,连接 , (保留作图痕迹,不写作法).(2)、求证:四边形是菱形.
(1)、尺规作图:作的平分线交于点D,连接 , (保留作图痕迹,不写作法).(2)、求证:四边形是菱形. -
6、(1)、计算:(2)、解方程:
-
7、 如图,正方形的边长为3,点在上且 , 点、分别为线段、上的动点,连接 , , , . 若在点、的运动过程中始终满足 , 则的最小值为.

-
8、 如图,点分别是正方形的边上的点,将正方形沿折叠,使得点的对应点在边上,若已知三角形的周长,则可以求出下列哪个数据( ).
 A、三角形周长 B、三角形的周长 C、三角形的面积 D、正方形的面积
A、三角形周长 B、三角形的周长 C、三角形的面积 D、正方形的面积 -
9、 如图,以为斜边的面积为2 ,以的各边为边分别向外作正方形, 过点作于点 , 过点作于点 , 则图中阴影面积为 ( )
 A、9 B、10 C、11 D、12
A、9 B、10 C、11 D、12 -
10、 如图,在中,的角平分线交于点 . 若平行四边形的周长为16,且 , 则的长度为( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
11、 在平行四边形中, , 则的度数为( )A、 B、 C、 D、
-
12、 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是 , 则射击成绩比较稳定的是( )A、甲 B、乙 C、丙 D、丁
-
13、 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
14、 如图,是的两条弦,于点 , 连结交于点 , 连结 , 设 .
 (1)、(用含的代数式表示);(2)、若 ,
(1)、(用含的代数式表示);(2)、若 ,①当时,求的值;
②若 , , 求的值.
-
15、 如图是某种固定式遮阳棚的实物图,某校数学兴趣小组对其进行实际测量,绘制了其横截面示意图,并得到以下数据:遮阳篷长为米,与水平面的夹角为 , 且靠墙端离地高为米.
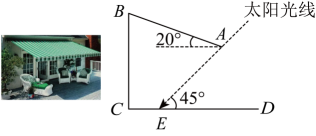 (1)、求遮阳棚外端点离地面的高度;(2)、若在某天的日照时间内,此处太阳光线与地面的夹角范围为至之间(包含和),求日照时间内阴影的最小值与最大值.(结果精确到 , 参考数据: , , )
(1)、求遮阳棚外端点离地面的高度;(2)、若在某天的日照时间内,此处太阳光线与地面的夹角范围为至之间(包含和),求日照时间内阴影的最小值与最大值.(结果精确到 , 参考数据: , , ) -
16、 如图,在中, , 点 , 分别为边、的中点,连接 , , 过点作交的延长线于点 , 连接 .
 (1)、求证:四边形是平行四边形;(2)、若 , , 求的长.
(1)、求证:四边形是平行四边形;(2)、若 , , 求的长. -
17、 《少年急救官生命教育安全课》以视频课的形式开播.某校为了解学生观看视频课的时长,随机抽取了部分学生观看视频课的时长t(单位:h)作为样本,将收集的数据整理后分为A,B,C,D,E五个组别,绘制成如下不完整的统计图表.
各组观看视频课时长频数分布表
组别
频数
A
5
B
12
C
D
15
E
8
各组观看视频课的时长扇形统计图

请根据以上信息回答下列问题:
(1)、本次调查的学生人数有人.(2)、扇形统计图中C组所在扇形的圆心角的度数是.(3)、若该校有1800名学生,估计该校学生观看视频课时长超过的人数. -
18、 解不等式组:.
-
19、 计算: .
-
20、 如图,在正方形纸片中,点E是的中点.将沿折叠,使点A落在点F处,连结.
 (1)、延长交于点G,则;(2)、若再将沿折叠,此时点的对应点恰好落在上.若记和重叠部分的面积为 , 正方形的面积为 , 则.
(1)、延长交于点G,则;(2)、若再将沿折叠,此时点的对应点恰好落在上.若记和重叠部分的面积为 , 正方形的面积为 , 则.