相关试卷

1、将等式a=b-1进行变形，其中变形正确的是（）

A、a-1=b B、-a=1-b C、a-3=b-2 D、2a=2b-1

查看解析
2、如图放置的圆柱体的主视图是（）

A、 B、 C、 D、

查看解析
3、在有理数2，-1，-5，0中，最大的数是（）

A、2 B、-1 C、-5 D、0

查看解析
4、实践探究.
【定义】在 $△ A B C$ 中，P是边AC上一点，若 $A B^{2} = A P \cdot A C$ ，则称点P是边AC关于边AB的“白银点”.

(1)、【概念理解】
如图(a)，请你利用尺规作图在 $△ A B C$ 中作出边AC关于边AB的“白银点”P.（不要求写作法，保留作图痕迹）

(2)、【性质应用】
如图(b)，在 $△ A B C$ 中，若 $A B = 4$ ， $B C = 6$ ， $A C = 8$ ，点P是边AC关于边AB的“白银点”，请你求出BP的值.

(3)、【拓展提升】
①如图(c)，在 $△ A B C$ 中，若 $A B = 4$ ， $B C = 6$ ， $∠ A = 2 ∠ C$ ，请你求出AC的值.
②如图(d)，在 $△ A B C$ 中，若 $A B = 4$ ， $A C = 8$ ， $∠ C = 4 5^{°} - \frac{1}{2} ∠ A$ ，请你求出BC的值.

查看解析
5、在物理实验中，光线从空气中射入液体中会发生折射现象. 某学习小组设计了如图所示的实验. 水槽横截面为矩形 MNFD， $M N = 80 c m$ ， O 为水槽水面 DF 的中点，水深 $D M = 20 c m$ . 如图（a），小明同学从高出水面 30 cm 的 A 处发出一束激光，射到水槽水面上的 O 处，光在水中的路径为 OB，C 为水槽底部 MN 的中点，测得 $B C = 10 c m$ .（图中点 M，C，B，N 在同一直线上；点 A，P，R，D，M 在同一直线上）

(1)、【问题初探】
如图（a）， $α$ ， $β$ 分别为入射角、折射角，则 $t a n α =$ ， $t a n β =$ .

(2)、【深入探究】
小组成员探究如何才能使折射光线经过点 C.
① 小张同学设计了如图（b）所示的实验，在保持光线出发点 A、入射角、折射角不变的条件下，通过增加水面高度，使得折射光线经过点 C，请求出增加的水面高度 DP 的值.
② 小刚同学设计了如图（c）所示的实验，在保持入射角、折射角不变的条件下，通过把光线的出发点从点 A 降至点 R，也能使得折射光线经过点 C. 请求出下降高度 AR 的值.

(3)、【问题拓展】
小组讨论后，认为在保持入射角、折射角不变的条件下，将光线出发点的高度降低 x cm，同时增加水面高度 y cm，也能使得折射光线经过点 C，请求出 y 与 x 之间的函数关系.

查看解析
6、如图，AB是 $⊙ O$ 的直径，点 $C$ 在 $⊙ O$ 上，分别连接CO、BC， $⊙ O$ 的切线AD与BC的延长线交于点 $D$ ， $E$ 是AD的中点，连接CE.

(1)、求证：CE是 $⊙ O$ 的切线；

(2)、若 $t a n D = \frac{3}{4}$ ， $B C = 6$ ，求四边形AOCE的面积.

查看解析

7、根据表中素材，完成任务.

素材1	某校为了引导学生学习人工智能知识、激发学生的创新思维，特开展“青少年人工智能挑战赛”活动.已知该活动设置“特等奖”和“优秀奖”两种奖项，需要购置的“特等奖”奖杯的单价比“优秀奖”奖杯的单价贵10元，用500元购进的“特等奖”奖杯的数量和用400元购进的“优秀奖”奖杯的数量相同.
素材2	学校的要求如下： ①此次活动的获奖总人数是30人. ②获得“优秀奖”的人数不超过“特等奖”人数的2倍.
⑴任务1	根据以上信息，请求出“优秀奖”和“特等奖”奖杯的单价.
⑵任务2	为响应降本增效方针，在满足要求的情况下尽量降低采购总费用，请求出此次颁奖所需奖杯的最低采购费用.

查看解析

8、科教兴国，科普为先. 某校组织七、八年级学生参加了“科技赋能，智行未来”科普知识竞赛，竞赛成绩分为A，B，C，D四个等级，对应等级得分依次记为10分，9分，8分，7分. 现从该校七、八年级学生中各随机抽取了40名学生的竞赛成绩进行整理，并绘制成了如下统计表和统计图（其中条形统计图不完整）.
年级
平均数
中位数
众数
七年级
8.5分
9分
a分
八年级
8.8分
b分
9分

(1)、根据以上信息填空：a= ， b=.

(2)、把条形统计图补充完整.

(3)、若该校七、八年级各有1000名学生参加了此次科普知识竞赛，请估计这两个年级成绩达到A等级10分的学生共有多少人？

查看解析
9、先化简，再求值： $(1 + \frac{1}{x - 1}) \div \frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ，其中 $x = 2$ .

查看解析
10、计算： $(3 - π)^{0} + | \frac{\sqrt{2}}{2} - 1 | - c o s 4 5^{°} + (- \frac{1}{2})^{- 2}$ .

查看解析
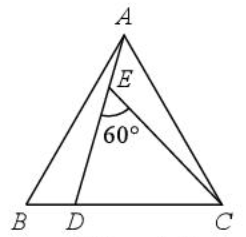
11、如图，在等边三角形ABC中，点D在边BC上， $B D = \frac{1}{3} C D$ ，连接AD，点E在线段AD上，连接CE.若 $A E = 2$ ， $∠ D E C = 6 0^{°}$ ，则AD的值为.

查看解析
12、如图， $△ A B C$ 的边AB与 $x$ 轴重合，已知点A的坐标为 $(2, 0)$ ， $∠ A B C = 9 0^{°}$ ， $∠ C A B = 3 0^{°}$ .将 $△ A B C$ 绕点A逆时针旋转 $6 0^{°}$ 得到 $△ A D E$ （点B，C的对应点分别为点D，E），若点C，E都在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则k的值为.

查看解析
13、关于x的方程 $m x^{2} + 4 x - 2 = 0$ 有两个不相等的实数根，请写出一个符合条件的m的值.

查看解析
14、周末，小亮打算在“甘坑古镇”、“大芬油画村”、“龙城公园”、“鹤湖新居”、“园山风景区”这五个景点中随机选择一个去游玩，恰好选中“龙城公园”的概率是.

查看解析
15、如图(a)，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ， CH为边AB的高， $A C = 3$ ， E， F分别为边AC， BC上的动点，且 $E H ⊥ F H$ .设CE的长为x， $△ C E F$ 的面积为y，图(b)为点E运动时y随x变化的关系图象，则AB的长度为（）

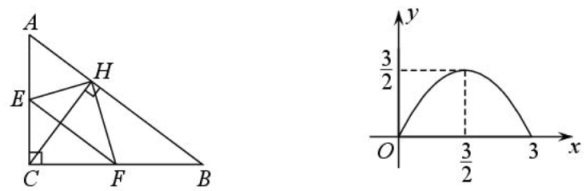A、4 B、5 C、 $3 \sqrt{2}$ D、6

查看解析
16、如图，某物理兴趣小组做小车从斜面下滑的实验时，将小车沿高度为h的斜面顶端向下滑，若斜面与水平面的夹角为 $α$ ，沿斜面下滑的时间为t，则小车在斜面上下滑的平均速度为（）

A、 $\frac{h}{t}$ B、 $\frac{h}{t \cdot s i n α}$ C、 $\frac{h}{t \cdot t a n α}$ D、 $\frac{h}{t \cdot c o s α}$

查看解析
17、《九章算术》中有一道题：“今有共买物，人出八，盈三；人出七，不足四. 问：人数、物价各几何？”其大意是：假设共同买东西，如果每个人出8钱，则买东西后还剩下3钱；如果每个人出7钱，则买东西时还差4钱. 问：人数、物价各是多少？设人数为x人，物价为y钱，那么下面所列方程正确的是（）

A、 ${\begin{array}{l} 8 x - 3 = y, \\ 7 x + 4 = y; \end{array}$ B、 ${\begin{array}{l} 8 x - 3 = y, \\ 7 x - 4 = y; \end{array}$ C、 ${\begin{array}{l} 8 x + 3 = y, \\ 7 x + 4 = y; \end{array}$ D、 ${\begin{array}{l} 8 x + 3 = y, \\ 7 x - 4 = y . \end{array}$

查看解析
18、若关于 x 的不等式组 ${\begin{array}{l} 3 x - 1 < 8 \\ x < m + 2 \end{array}$ 的解集为 $x < 3$ ，则 m 的取值范围是（）

A、 $m \geq 3$ B、 $m \leq 3$ C、 $m \geq 1$ D、 $m \leq 1$

查看解析
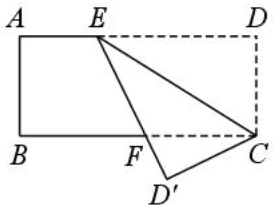
19、如图，在矩形 ABCD 中，点 E 在边 AD 上，连接 CE，将 $△ C D E$ 沿 CE翻折得到 $△ C D^{'} E$ ，点 D 的对应点为点 D'，DE 交 BC 于点 F. 若 $∠ B F E = 6 4^{°}$ ，则 $∠ D E C =$ （）

A、 $3 2^{°}$ B、 $6 4^{°}$ C、 $5 8^{°}$ D、 $2 6^{°}$

查看解析
20、下列计算正确的是（）

A、 $3 a b - a b = 3$ B、 $(a - b)^{2} = a^{2} - b^{2}$ C、 $\sqrt{(a + b)} = \sqrt{a} + \sqrt{b}$ D、 $2^{- 2} = \frac{1}{4}$

查看解析

上一页 927 928 929 930 931 下一页跳转

年级	平均数	中位数	众数
七年级	8.5分	9分	a分
八年级	8.8分	b分	9分