-
1、如图1，点O，F分别为凸透镜MN的光心与焦点，直线OF为凸透镜的主光轴，.根据科学原理，若从光源A射出的光线AC与OF平行，其折射光线必过点F；若从光源A射出的光线过点O，则光线不发生偏折，继续沿原方向传播.作于点B，设 ， （其中）.
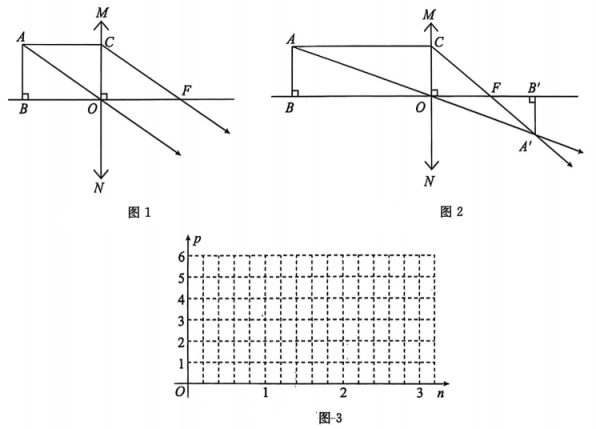(1)、如图1，若 ， 判断光线AO，CF的位置关系，并说明理由.(2)、如图2，若 ， 光线AO，CF交于点A'，于点B'，设.①当n=2时，求p的值；
②求p关于的函数关系式，并在图3坐标系中画出该函数图象；
③比较A'B'与AB的大小.
-
2、二次函数的图像经过点（0，-3）.(1)、求a的值.(2)、当时，该函数的最大值减去最小值的差为 ， 当时，该函数的最大值减去最小值的差为.
①若 ， 求m的取值范围；
②是否存在？若存在，请求出m的取值范围；若不存在，请说明理由.
-
3、如图，AB为⊙O的直径，点C在⊙O外，AD平分∠BAC，交BC于点D，交⊙O于点E，DF⊥AC于点F，AF=AB.
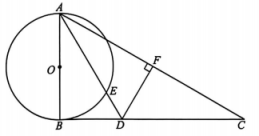(1)、求证：BC是⊙O的切线；(2)、若CF=AF=6，求弧BE的长度. -
4、 “黄金1号”玉米种子的价格为5元/kg，如果一次性购买2kg以上的种子，超过2kg的部分打8折.设“黄金1号”玉米种子的一次性购买量为x（单位：kg），相应的付款金额为y（单位：元）.(1)、①完成下表：
购买量x/kg
0.5
1
1.5
2
2.5
3
…
付款金额y/元
2.5
5
7.5
▲
▲
14
…
②求y关于x（x≥2）的函数解析式；
(2)、“黄金2号”玉米种子的价格为a元/kg，且始终不打折.若两种玉米种子的一次性购买量相同，则“黄金1号”玉米种子的付款金额始终要高于“黄金2号”，请直接写出ａ的最大值. -
5、规定乒乓球直径的标准尺寸为40mm，最大可以是40.2mm，最小可以是39.8mm，在此范围内的都是优等品.某车间生产了2000个乒乓球，质检员从中随机抽取100个乒乓球检测直径，数据整理如下表.
直径/mm
39.7
39.8
39.9
40.0
40.1
40.2
40.3
…
频数/个
8
22
11
11
27
8
13
…
(1)、被抽查的100个乒乓球的直径数据中，中位数、众数分别是多少？(2)、该车间生产的2000个乒乓球中，优等品大约有多少个？ -
6、小甬按如图方式测量旗杆高度AB，将A处的绳子笔直拉至地面C处，使B，C间距离等于小甬直立时的眼睛离地高度，在C处放置一块直角三角板PMN，使直角顶点P落在C处，边PN与绳子重合，随后小甬后退至D处直立，使眼睛E与点M，P在同一直线上.小甬认为CD的长等于旗杆高度AB，你认同他的观点吗？请说明理由．
-
7、
-
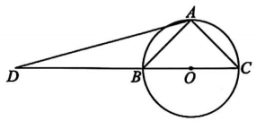
8、如图，点A在以BC为直径的⊙O上，点D在CB的延长线上.若∠DAB=30°，DB：BC=4：3，则tan∠ACB=.
-
9、如图，在△ABC中，∠B=2∠C，AD⊥BC于点D.若△ABC的周长为20，CD=6，则AC的长为.
-
10、已知关于的一元二次方程（x+1）（x-5）=k有一个实数根x1=-2，则它的另一个实数根x2=.
-
11、小钱、小塘玩“石头、剪刀、布”游戏，若两人同时随机各出一个手势，则两人分出胜负的概率为.
-
12、不等式2x-3<2的解集为.
-
13、因式分解：4x2-9=.
-
14、如图，在△ABC中，AB=10，AC=8.在高线AD所在直线上任取一点P（不与点A，D重合），连结PB，PC，则PB2-PC2的值为（ ）
A、6 B、18 C、36 D、72 -
15、地震规模大小通常用里氏震级表示，一次地震的里氏震级M与距离震中100km处测得的最大振幅A（单位：μm）之间的关系为10M=kA（k为常数）.若里氏震级M提高2级，则距离震中100km处测得的最大振幅A将增大到原来的（ ）A、100倍 B、20倍 C、10倍 D、2倍
-
16、对一个四边形的特征描述如下：①有一组邻边相等；②对角线互相平分；③对角线互相垂直.选择其中两个特征作为题设，余下的特征作为结论组成三个命题，其中真命题的个数为（ ）A、0个 B、1个 C、2个 D、3个
-
17、如图，在△ABC中，AB=AC，∠A=40°.以点B为圆心，BC为半径画弧，与AB交于点D，连结CD，则∠ACD的度数为（ ）
A、12° B、15° C、18° D、20° -
18、如图，数轴上的点A，B，C，D分别表示数a，b，c，d.若AB=1，CD=2，a+d=7，则b+c的值为（ ）
A、4 B、5 C、6 D、7 -
19、将数组：5，8，4，3，10中的每一个数加1，得到一个新数组.将原数组和新数组的平均数分别记为 ， ， 方差分别记为 ， ， 下列结论中，正确的是（ ）A、 ， B、 ， C、 ， D、 ，
-
20、化简的结果为（ ）A、 B、 C、1 D、-1