-
1、综合与实践
【主题】自制环保笔筒
【素材】如图,一个直径为 , 高的纸筒卷,一张长 , 宽的包装纸,一张边长为的小正方形纸板,一根装饰绳子,一把剪刀,一瓶固体胶.

【实践操作】
步骤1:在包装纸上用剪刀裁剪出一张刚好能与纸筒卷外表面紧密贴合的纸;
步骤2:用固体胶把包装纸紧密地贴在纸筒卷外表面;
步骤3:用固体胶把装饰用的绳子粘在纸筒外面;
步骤4:用固体胶把小正方形纸板粘在纸筒卷的底部,得到一个形如2图所示的环保笔筒.

【实践探索】
(1)、求出步骤1中裁剪出的包装纸的面积;(结果保留)(2)、如3图,如果想要绳子缠绕笔筒圈,正好从点绕到正上方的点,求所需绳子的最短长度.(结果保留和根号)
-
2、如图,双曲线的图象与一次函数的图象交于 , 两点.
 (1)、求 , 的值,并求反比例函数的解析式;(2)、设直线与轴交于点 , 若为轴上一点,当的面积为时,求点的坐标.
(1)、求 , 的值,并求反比例函数的解析式;(2)、设直线与轴交于点 , 若为轴上一点,当的面积为时,求点的坐标. -
3、“国家喊你该减肥了”,国家卫生健康委联合民政部等部门启动实施了“体重管理年”行动.某社区积极响应,安装了两款健身器材,方便居民健身活动,并对两款健身器材进行了满意度测评,社区工作人员从居民对两款健身器材的满意度评分中各随机抽取份,对数据进行整理、描述和分析.(评分分数用表示,分为四个等级:不满意 , 比较满意 , 满意 , 非常满意 , 单位:分)抽取的对款健身器材的评分数据中“满意”包含的所有数据: , , , , , ;抽取的对B款健身器材的评分数据: , , , , , , , , , , , , , , , , , , , .
抽取的对款健身器材的满意度评分统计表
健身器材
平均数
中位数
众数
“非常满意”所占百分比

根据以上信息,解答下列问题:
(1)、填空:______;(2)、若有名居民对款健身器材进行评分,请你估计“满意”的有多少人;(3)、社区甲乙两人进行健身活动,用列表或树状图求甲选器材乙选器材的概率. -
4、如图,在中,点E为中点,交于点D.
 (1)、请用无刻度的直尺和圆规作 , 使 , 且射线交于点F(保留作图痕迹,不写作法);(2)、试判断(1)中得到的四边形的形状,并说明理由.
(1)、请用无刻度的直尺和圆规作 , 使 , 且射线交于点F(保留作图痕迹,不写作法);(2)、试判断(1)中得到的四边形的形状,并说明理由. -
5、为了贯彻落实“阳光2小时”,清远某学校准备一次性购买若干个足球和篮球,已知用900元购买足球的数量是用600元购买篮球数量的2倍,且篮球的单价比足球多30元,求足球与篮球的单价.
-
6、基本概念与代数推理:(1)、若两个二项式相乘 , 刚好满足平方差公式,则括号里面可填______;(2)、请说明,不管取何值,二次根式有意义.
-
7、在数学课上,某同学用一张如图所示的长方形纸板制做了一个扇形,并由这个扇形,围成一个圆锥模型,若扇形的圆心角为 , 圆锥的底面半径 , 则此圆锥的高为 .

-
8、 .
-
9、如图,二次函数的图象与x轴交于点 , 与y轴交于点B,对称轴为直线 , 下列四个结论:①该图象经过点;②;③;④ , 其中正确结论的个数为( )
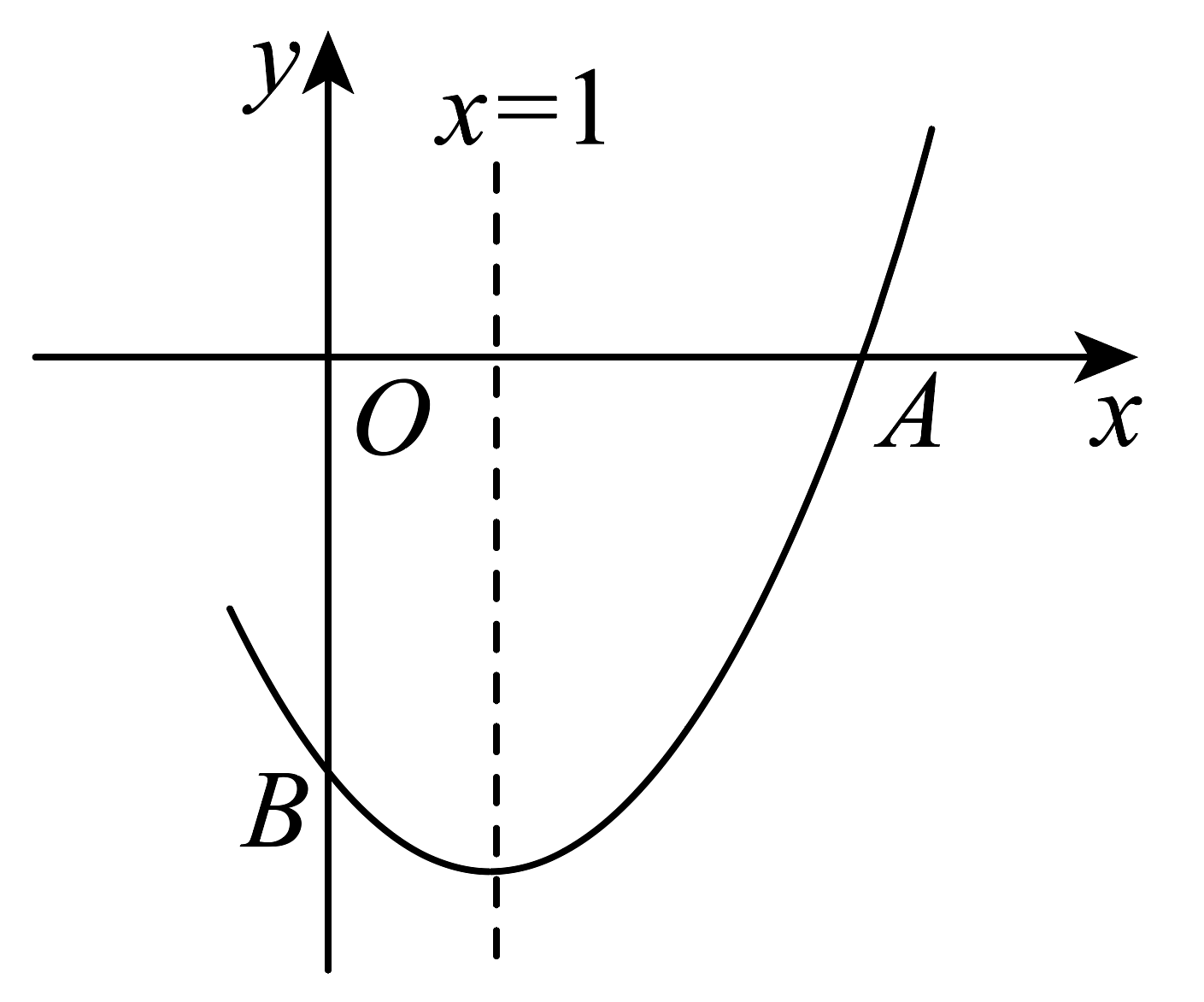 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
10、如图,在矩形中, , , 交于点 , 交于点 , 则线段的长是( )
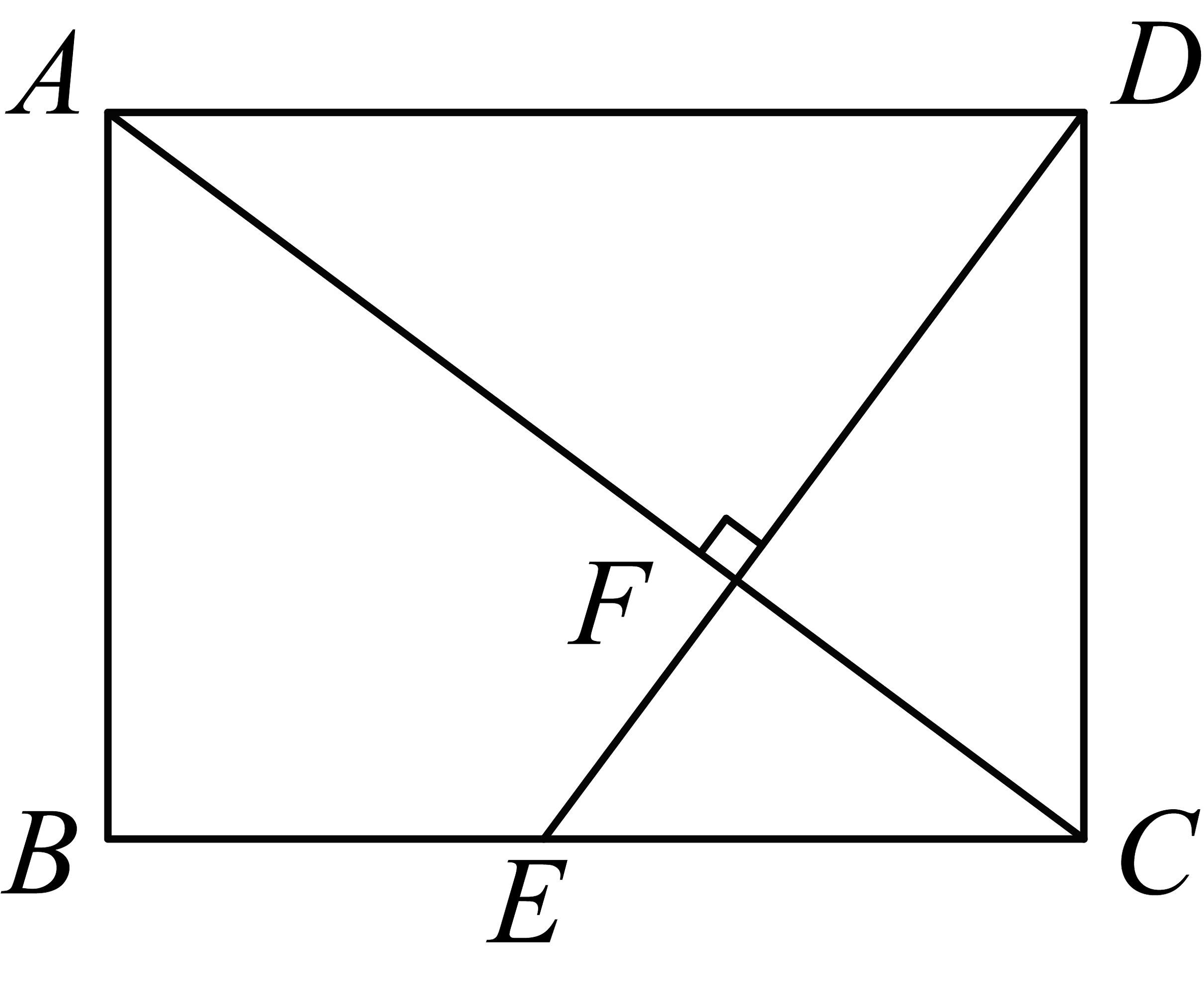 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,小明参加骑行活动,骑行中遇到斜坡路段,小明沿斜坡从A点骑行到B点的路程为 , 其上升的垂直高度为 , 则斜坡的坡度为( )
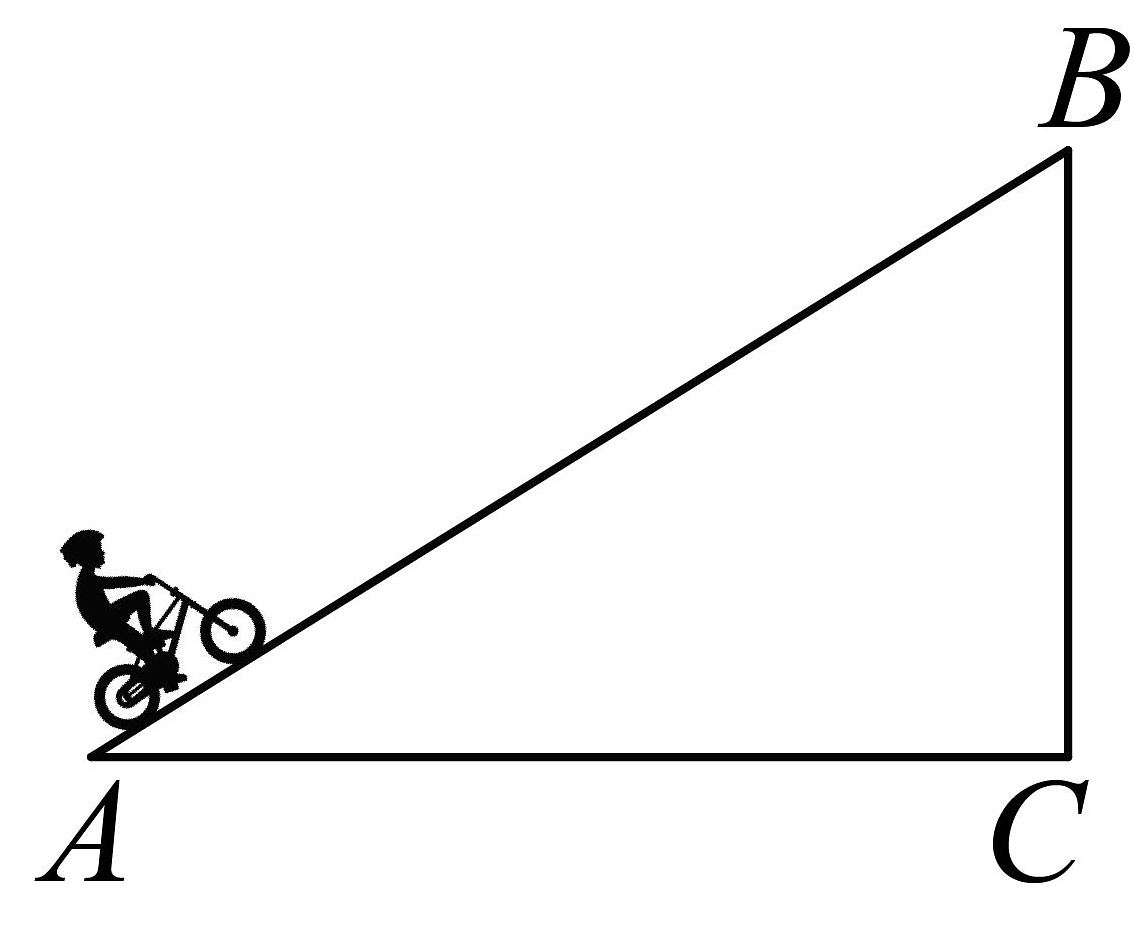 A、 B、 C、 D、
A、 B、 C、 D、 -
12、对于一次函数的相关性质,下列描述错误的是( )A、函数图象经过第一、二、三象限 B、函数图象经过点 C、函数图象与y轴的交点坐标为 D、y随x的增大而减小
-
13、如图,直线 , 直线与直线分别相交于点和 , , 垂足为点 , 若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、下列式子计算正确的是( )A、 B、 C、 D、
-
15、截止至2024年12月底,广东清远市的常住人口约为397万人,397万用科学记数法表示为( )A、 B、 C、 D、
-
16、下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
17、【问题提出】在旋转专题复习课中,王老师引导同学们积极探究以下问题:
将一大一小两个等腰直角三角板如图1放置, , 点F在内,连接并延长到点E,使 , 连接 , , . 探究线段与的关系.
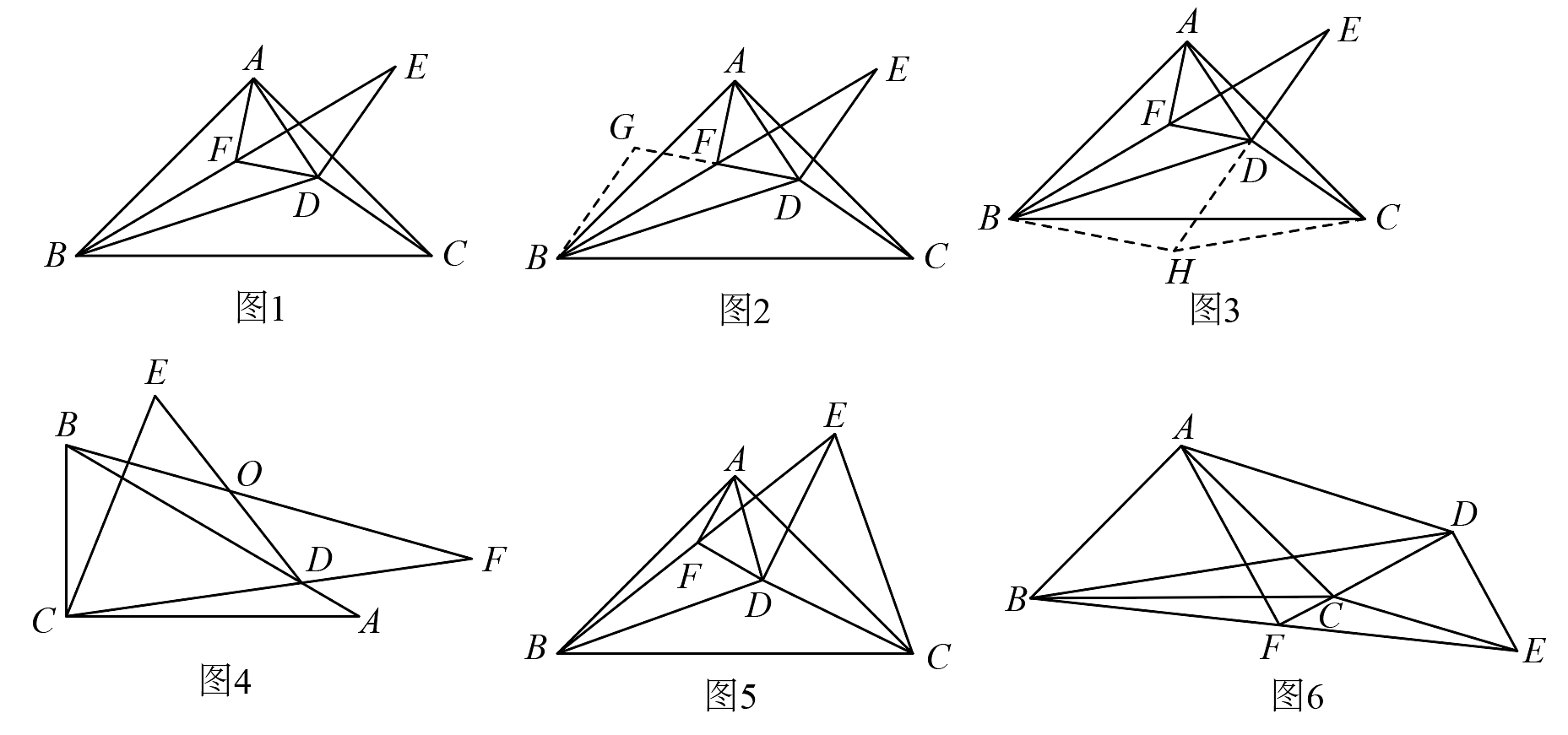
【思路探究】“勤学小组”的解题思路:将线段借助平行线进行平移,如图2,过点B作平行交的延长线于点G,这样可以将证明和的关系转化为和的关系;
“善思小组”的解题思路:结合F为的中点构造三角形的中位线,如图3,过点B作平行交延长线于点H,从而借助三角形中位线性质,将和的关系转化为和的关系.
(1)请你写出线段与的数量关系________,位置关系________,并证明线段与的数量关系(写出一种方法即可);
【思维训练】王老师为了进一步让学生体会平行线在图形证明中的作用,又出示了下列问题:
(2)如图4,在中, , , D为上一点,将绕点C逆时针旋转得到 , 连接 , , O为中点,连接并延长交的延长线于点F,若 , 探究 , , 之间的数量关系__________,并说明理由;
【能力提升】
(3)“创新小组”的同学在【问题提出】的基础上对该问题又进一步拓展:连接 , 若F为平面内一点, , , , 其他条件不变,请直接写出的值(参考图5、图6).
-
18、【问题背景】
人们从城市中的一点到另一点时,通常只能沿着城市中的街道行走.因此,人们发现,用19世纪数学家闵可夫斯基提出的曼哈顿距离来计算城市内街道上两点之间的距离更符合生活现实.曼哈顿距离(简称为“曼距”的定义如下:坐标平面内的两点 , , , 之间的距离为 . 例如,在平面直角坐标系中,点与点之间的“曼距” .
【初步理解】
(1)在一座理想的棋盘式布局的城市内,“110”的调度员收到信息,有一个突发事故发生在处.而在该地区附近有两辆警车,车位于处,车位于处,那么以“曼距”大小衡量,按“就近优先出警”的原则,应该派 车(填或前去处理事故.
(2)如图1,正方形的中心位于坐标原点 , 四个顶点均位于坐标轴上,且 . 则下列说法:
①若点是正方形一边上的一点,则;②若点是正方形内的一点,则;
③若点是正方形外的一点,则;④若点是正方形内的一点,则 .
其中不正确的是 (填序号).
【探究应用】
(3)如图2,某消防支队位于坐标原点 , 轴是一条城市主干道,“月牙湖”位于城市边陲,其西、南岸可近似看作一段圆弧.已知圆弧形湖岸经过 , , 三点.今该消防支队要在湖岸边,建一个训练基地(记为点 , 为使该消防支队官兵,平时前往基地参训时的“曼距”最短,需探究:点的位置应选在何处?请作答以下问题:
①圆弧所在的圆的圆心的坐标为 , 该圆的半径大小为 ;
②请利用网格格点,在图2中,画出使最小时点的位置(不要求证明);
③的最小值为 .

-
19、“端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒的利润率不低于 , 且每盒售价不得高于80元.根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒.设每盒售价为x元,日销售量为p盒.(1)、当时,________;(2)、当每盒售价定为多少元时,日销售额y(元)最大?最大日销售额是多少元?
-
20、在实验教育集团“学习总理精神,担当时代责任”主题演讲比赛中,A、B两所学校各有10名学生进入决赛,现对他们的成绩(满分100分)进行整理分析,得到如图表信息:

平均数
众数
中位数
A学校
85.5
80
n
B学校
85.5
m
86
根据以上信息,回答下列问题:
(1)、填空:________,________;(2)、A、B两所学校决赛成绩的方差分别记为、 , 请判断_______(填“”“”或“”);(3)、本次比赛的前4名分别来自A、B两所学校,该区决定从这4位学生(A校3位,B校1位)中随机选取2位学生参加市级竞赛,求选中的两位学生恰好在同一学校的概率.