-
1、已知抛物线与轴交于、两点(点在点的左侧),与轴交于点 , 直线过点 . 与抛物线交于、两点,且 , .(1)、求抛物线的对称轴;(2)、求 , , 的值;(3)、点是下方抛物线上一点,过作轴交抛物线于点 , 交于点 , 求的最大值.
-
2、如图,在正方形中,点是上一动点(不与点 , 重合),连接 , 将绕点在平面内按顺时针方向旋转至位置,连接 , 交于点 .
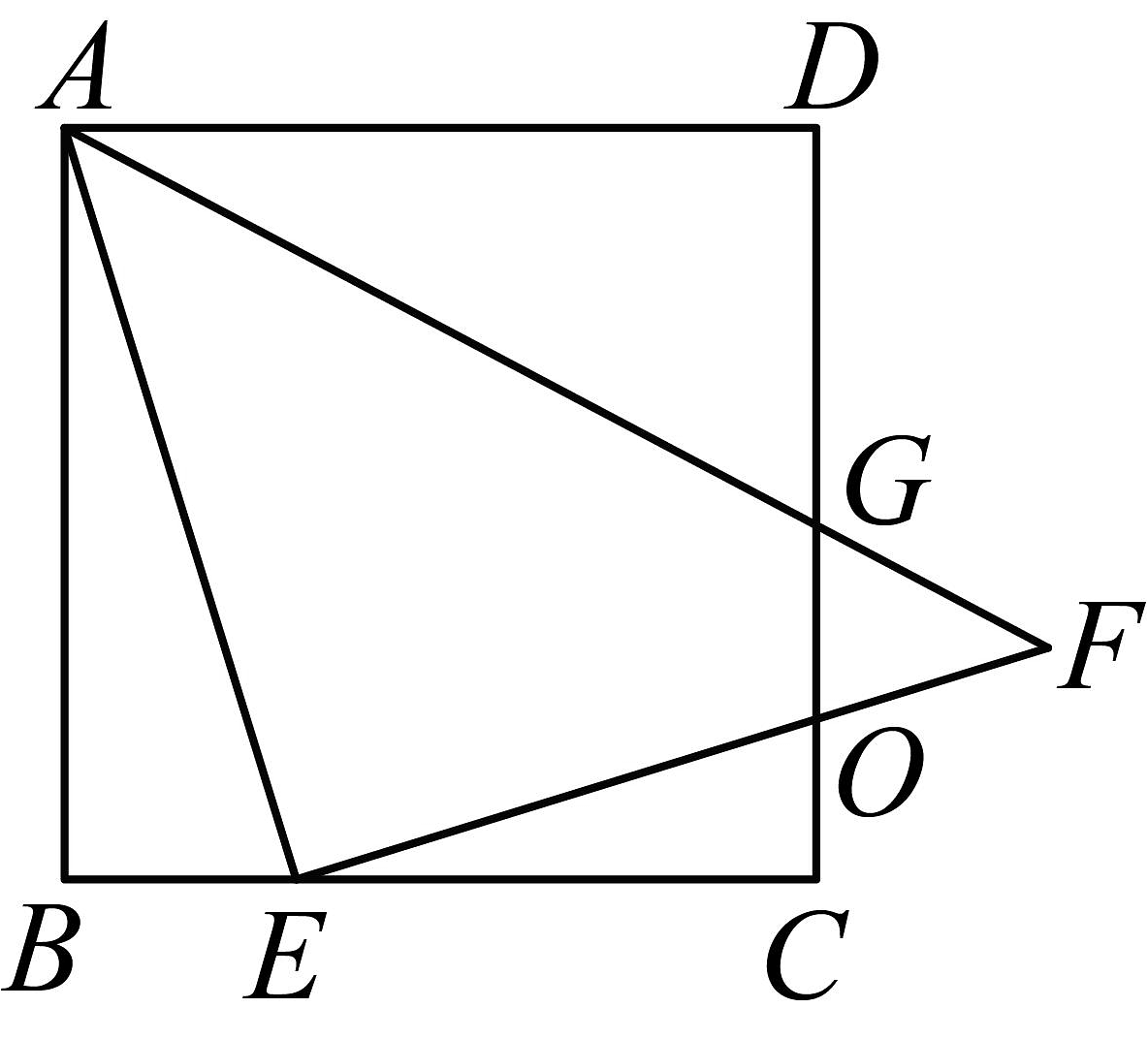 (1)、求证:;(2)、过点作于点 , 其延长线交于点 .
(1)、求证:;(2)、过点作于点 , 其延长线交于点 .①连接 , 求证:平分;
②当时,求的值.
-
3、如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境,受桔槔的启发,某数学兴趣小组组装了以下装置,通过实验收集了大量数据,对数据的整理和分析,发现的长度和重物的质量之间近似存在一个函数关系,部分数据如下表:


…
10
16
20
25
40
50
…
…
8
5
4
3.2
2
1.6
…
(1)、在图1中描出表中数据对应的点;(2)、根据表中数据,从和中选择一个函数模型,使它能近似的反映重物的质量为和的长度为的函数关系,并求出这个函数的解析式(不要求写出的取值范围);(3)、在(2)的条件下,若点的坐标为 , 点的坐标为 , 在(2)中所求函数的图象上存在点 , 使得 , 请求出所有满足条件的点的坐标. -
4、如图,内接于是的直径,是的中点,连接 .
 (1)、请用无刻度的直尺和圆规,过点作直线垂直于直线(保留作图痕迹,不写作法);(2)、若(1)中所作的直线与直线交于点 . 与的延长线交于点 .
(1)、请用无刻度的直尺和圆规,过点作直线垂直于直线(保留作图痕迹,不写作法);(2)、若(1)中所作的直线与直线交于点 . 与的延长线交于点 .①判断直线与的位置关系,并说明理由;
②若 , 求的长.
-
5、在数学综合与实践活动课上,老师组织同学们开展以“测量小树的高度”为主题的探究活动.
【小组1】查阅学校资料得知小树前的教学楼高度为24米,如图1,某一时刻测得小树、教学楼在同一时刻阳光下的投影长分别是米,米.
【小组2】借助皮尺和测角仪,如图2,已知测角仪离地面的高度米,在处测得小树顶部的仰角 , 测角仪到树的水平距离米.
 (1)、请根据小组1的数据求小树的高度;(2)、请根据小组2的数据求小树的高度(结果保留整数, , ).
(1)、请根据小组1的数据求小树的高度;(2)、请根据小组2的数据求小树的高度(结果保留整数, , ). -
6、已知 .(1)、化简;(2)、若数轴上点、表示的数分别为、 , 且 , 求的值.
-
7、如图, . 求证:四边形是平行四边形.

-
8、如图,是菱形的对角线,关于的轴对称图形为 , 且 . 以下结论正确的是 .
为等腰直角三角形;;;④;⑤ .

-
9、已知是方程的一个根,则代数式的值为 .
-
10、我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”.如图.在设计人体雕像时,为了增加视觉美感利用黄金分割法,将雕像分为上下两部分,其中为的黄金分割点 , 已知长为2米,则的长是米.

-
11、分式方程的解为 .
-
12、如图,等边三角形的顶点 , 点在第一象限内,点在边上且 , 点为边上一动点(不与点重合),连接 , 将沿折叠得到 , 当的面积最小时,点到的距离为( )
 A、 B、2 C、 D、
A、 B、2 C、 D、 -
13、已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )A、 B、 C、且 D、且
-
14、甲、乙两家酒店规模相当,去年月的月盈利折线统计图如图所示.下列说法中,不正确的是( )
 A、甲酒店每月盈利呈现不断增长的趋势 B、乙酒店经营状况有可能很快超过甲酒店 C、甲酒店月盈利的平均数大于乙酒店月盈利的平均数 D、甲酒店月盈利的方差小于乙酒店月盈利的方差
A、甲酒店每月盈利呈现不断增长的趋势 B、乙酒店经营状况有可能很快超过甲酒店 C、甲酒店月盈利的平均数大于乙酒店月盈利的平均数 D、甲酒店月盈利的方差小于乙酒店月盈利的方差 -
15、如图,是红军长征路线图,若表示会宁会师的点的坐标为 , 则表示瑞金的点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、在 , 0, , 2这四个数中,无理数是( )A、 B、 C、0 D、2
-
17、下列四个前沿的大模型的图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如图1).并绘制出不完整的条形统计图(如图2).
成绩
频数
百分比
不及格
3
a
及格
b
良好
45
c
优秀
32
图1 学生体质健康统计表
 (1)、图1中________,________,________;(2)、请补全图2的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;(3)、为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会.请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率.
(1)、图1中________,________,________;(2)、请补全图2的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;(3)、为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会.请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率. -
19、如1图,在中, , , 点、分别在边、上, , 连接 , 点、、分别为、、的中点.
 (1)、观察猜想:1图中,数线段与的量关系是______,位置关系是______;(2)、探究证明:如2图在中, , , 点、分别在边、上, , 连接 , 点、、分别为、、的中点.把绕点逆时针方向旋转到3图的位置,连接 , , , 判断的形状,并说明理由;(3)、拓展延伸:在(2)的基础上,把绕点在平面内自由旋转,若 , , 请你求出周长的最大值.
(1)、观察猜想:1图中,数线段与的量关系是______,位置关系是______;(2)、探究证明:如2图在中, , , 点、分别在边、上, , 连接 , 点、、分别为、、的中点.把绕点逆时针方向旋转到3图的位置,连接 , , , 判断的形状,并说明理由;(3)、拓展延伸:在(2)的基础上,把绕点在平面内自由旋转,若 , , 请你求出周长的最大值. -
20、抛物线与x轴交于A,两点(A在B的左侧),与y轴交于点 . 点P在抛物线上,连接 .
 (1)、求抛物线的解析式;(2)、如1图,若点P在第四象限,点D在线段上,连接并延长交x轴于点E,若 , 连接 , 记的面积为 , 的面积为 , 当时,求点P的坐标;(3)、如2图,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段交于点G,当时,求点P的横坐标.
(1)、求抛物线的解析式;(2)、如1图,若点P在第四象限,点D在线段上,连接并延长交x轴于点E,若 , 连接 , 记的面积为 , 的面积为 , 当时,求点P的坐标;(3)、如2图,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段交于点G,当时,求点P的横坐标.