-
1、2024年5月8日,云岩区中小学科学教育实验区建设正式启动,标志着我区在科学教育领域迈出了重要一步.某校为加强实验教学,确保每位学生都能动手操作、亲身体验,开设了七年级生物实验课,要求七年级学生每人在以下五个生物实验中选择一个进行研究(每人只选一个).
实验名称:
A.研究鱼游泳时鱼鳍的作用;
B.研究小鼠走迷宫的学习行为;
C.观察家蚕的完全变态发育过程;
D.观察青蛙的变态发育过程;
E.观察蚂蚁的信息交流.
为了解学生的选择情况,现从该校七年级随机抽取部分学生进行问卷调查,根据学生的选择,小红绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题:
 (1)、此次共调查学生 人;(2)、将条形统计图补充完整;生物实验D所在扇形的圆心角为 ;(3)、若该校七年级共有学生800人,请估计选择生物实验E的学生有多少人?
(1)、此次共调查学生 人;(2)、将条形统计图补充完整;生物实验D所在扇形的圆心角为 ;(3)、若该校七年级共有学生800人,请估计选择生物实验E的学生有多少人? -
2、如图,在中, , 点D,E分别是 , 的中点,连接 , 延长至点F,使 , 连接 .
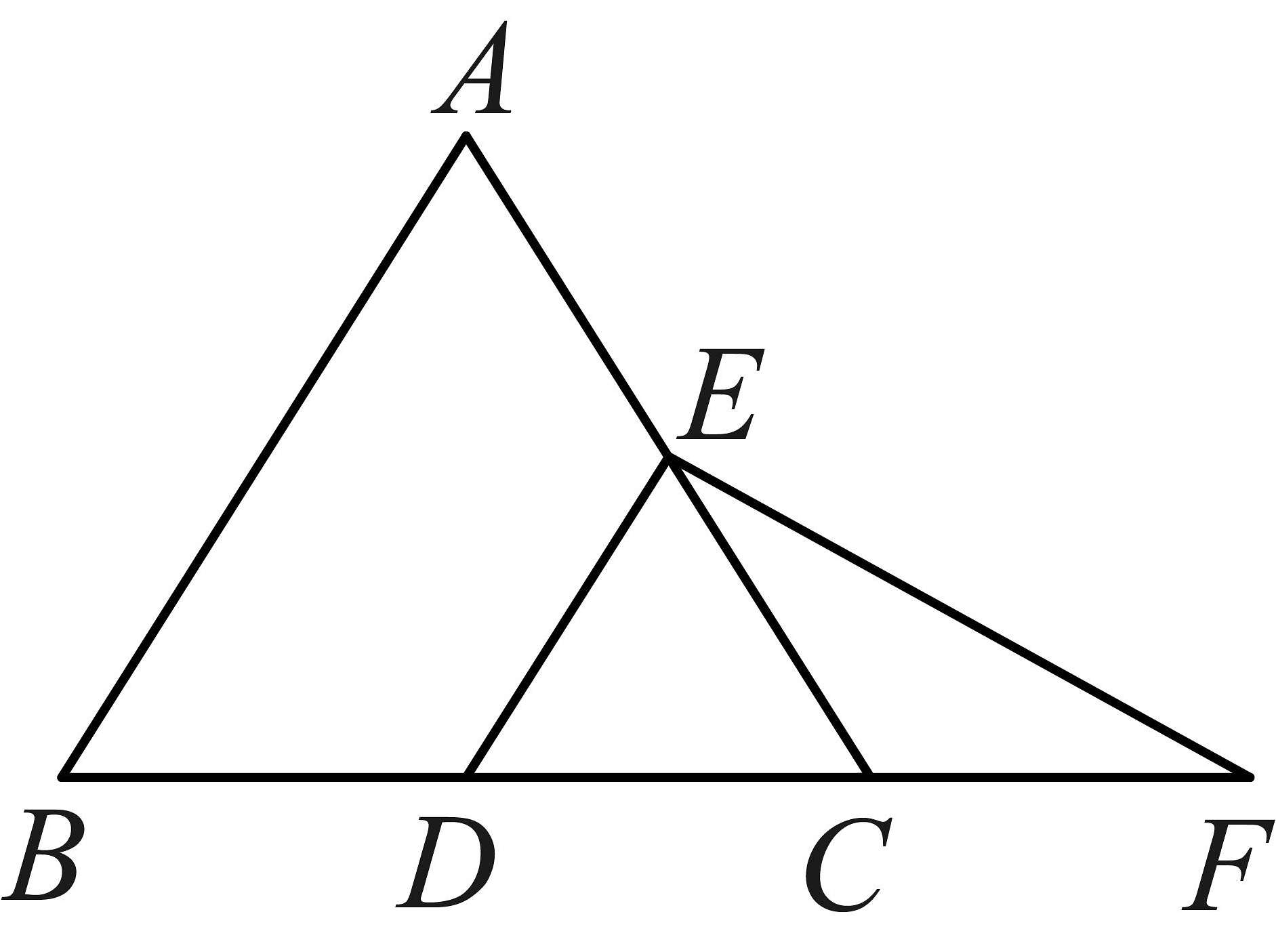 (1)、求证:是等腰三角形;(2)、已知 , 求的度数.
(1)、求证:是等腰三角形;(2)、已知 , 求的度数. -
3、
综合与实践:制作简易计时器
【问题情境】
某小组同学根据古代计时器“漏壶”的原理制作了如图所示的简易计时器,该计时器由一个圆锥和一个圆柱组成,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中.
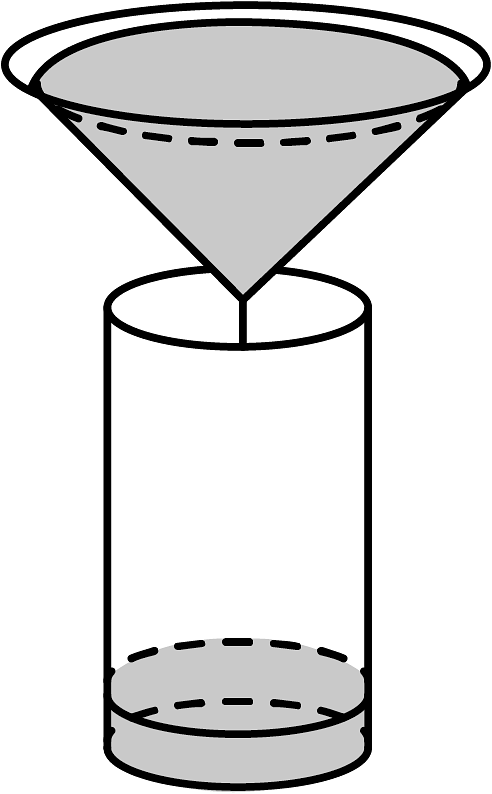
【实验观察】表格记录的是圆柱容器液面高度y()与时间x()的数据:
记录次数
第一次
第二次
第三次
第四次
第五次
时间x()
1
2
3
4
5
圆柱容器液面高度y()
2
4
6
4
10
【探索发现】根据上述的实践活动,该小组同学发现y与x之间满足一次函数关系,请解决以下问题:
(1)根据表中的数据在图中描点:小组长发现其中有一次数据记录错误,请你指出记录错误的是第 次:
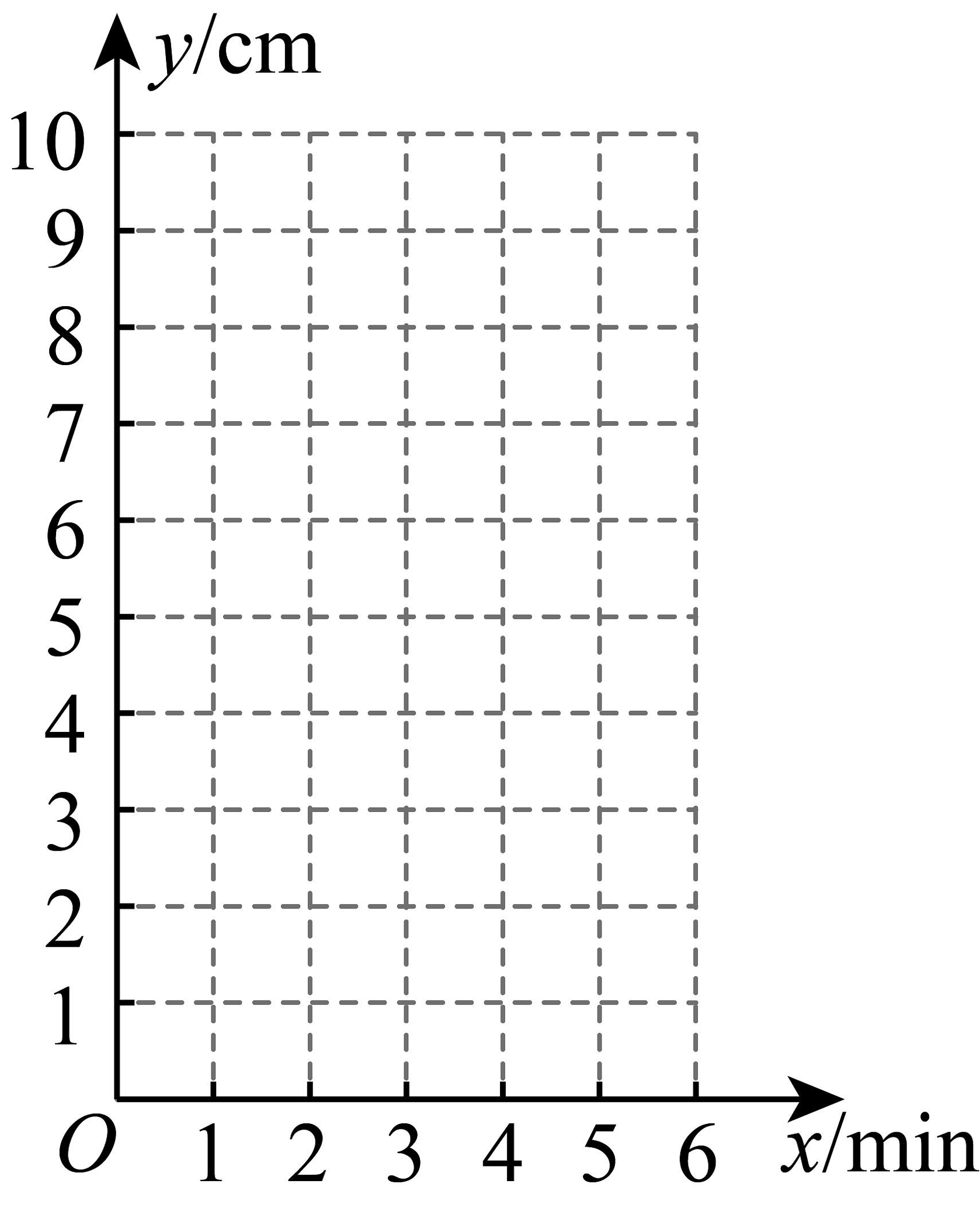
【结论应用】
(2)已知圆柱容器液面的最大高度能达到 , 则这个简易计时器最多可计时多少分钟?
-
4、(1)计算:;
(2)如图,数轴上的点A表示数 , 点B表示数 , 且点A始终在点B的左侧,求满足条件的x的取值范围.

-
5、如图,中, , 的外角平分线交于点A,过点A分别作直线的垂线,B,D为垂足.已知 , 则的值为 .
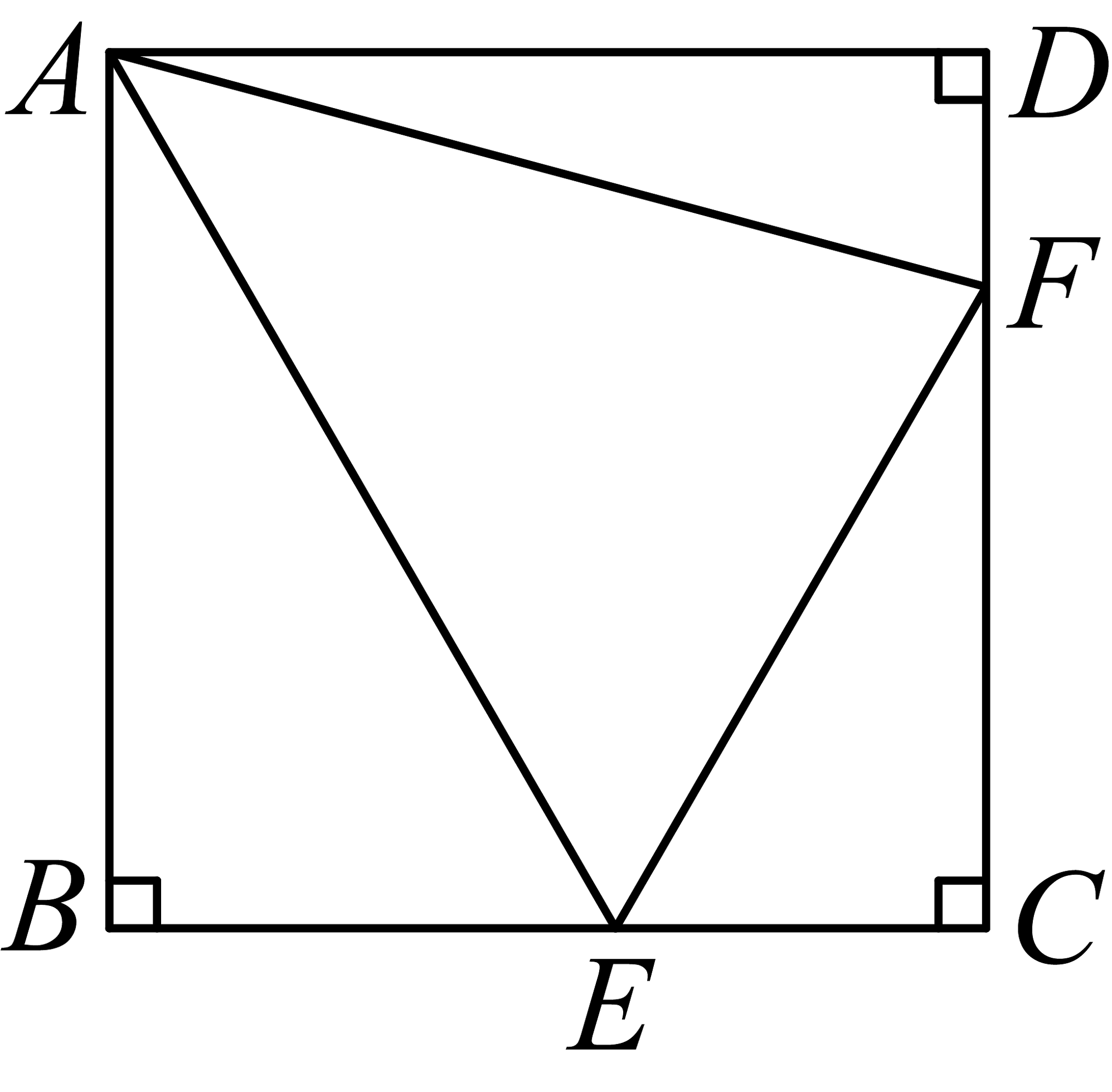
-
6、若分式无意义,则x的值为 .
-
7、如图,已知线段 . 按下列步骤作图:①分别以点A,B为圆心、以的长为半径作弧,两弧交于点C;②连接 . 观察尺规作图的痕迹,的度数为 .
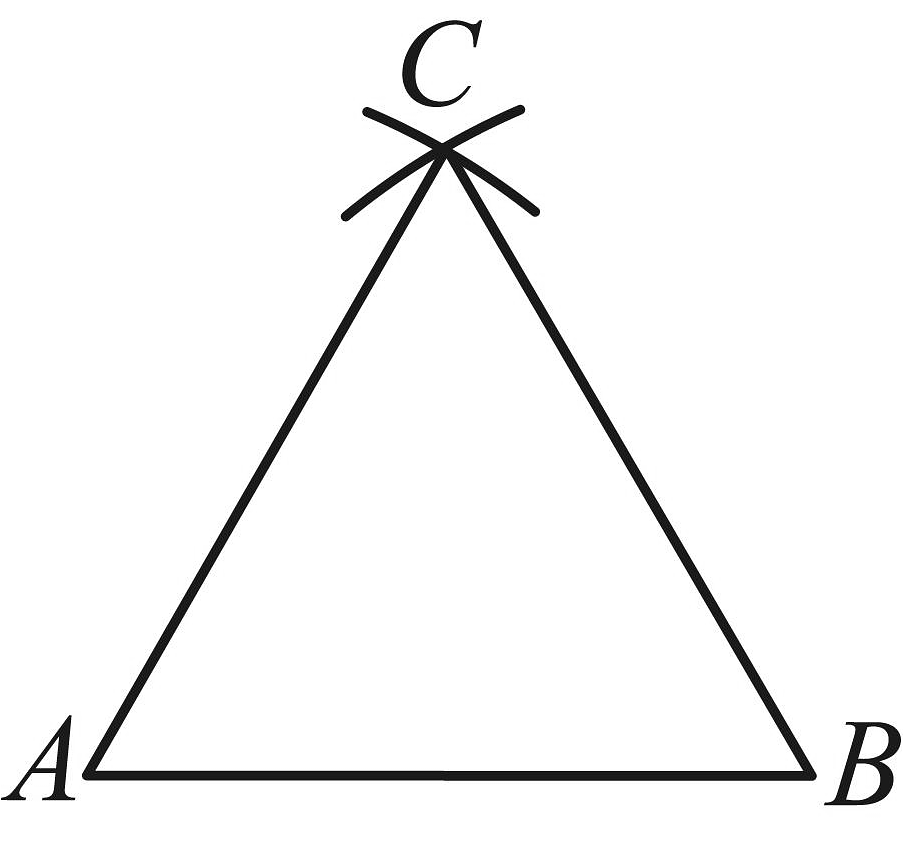
-
8、如图,在平面直角坐标系中,点在反比例函数(k为常数,)的图象上.将直线沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若 , 则点B的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、中华美食讲究色香味美,优雅的摆盘能让美食锦上添花.图①外围的每一个拼盘的形状都是扇形的一部分,图②是其中一个的示意图(阴影部分为拼盘).测量得到 , , , 则图②所示的拼盘面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、根据表格中的信息,估计一元二次方程的一个解的范围是( )
x
0
1
2
5
A、 B、 C、 D、 -
11、一次函数(k,b为常数,)的图象如图所示,则关于x的不等式的解集为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、在剪纸活动中,小华想用一张矩形纸片剪出一个正八边形,如图,正八边形的一边与矩形的边重合,则的大小为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、甲、乙、丙、丁四名射击运动员各进行20次射击测试,他们的测试平均成绩相同,方差分别是 , , , , 则这四名射击运动员中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁
-
14、用加减消元法解方程组时,将可得( )A、 B、 C、 D、
-
15、“加榜梯田”“从江鼓楼”“岜(bā)沙苗寨”是从江县著名旅游景点.以“从江鼓楼”为原点建立直角坐标系,若“岜沙苗寨”的坐标为 , 则“加榜梯田”的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、将分别标有“多”“彩”“贵”“州”汉字的四个小球装在一个不透明的口袋中,这些小球除汉字外都相同,随机摸出一球,摸到标有“贵”字小球的概率是( )A、 B、 C、 D、
-
17、计算的结果是( )A、 B、 C、 D、
-
18、窗花是我国最具代表性的民间艺术之一.下列窗花图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、中国是最早采用正负数表示相反意义的量的国家.如果零上记作 , 那么零下记作( )A、 B、 C、 D、
-
20、在平面直角坐标系中,点O是坐标原点,抛物线(b是常数)经过点 , 点M在抛物线上,横坐标为m,点N的横坐标为 , 纵坐标与点M的纵坐标相同,点A在y轴上,纵坐标为m.当点M和点A的纵坐标不相等时,作点A关于点M的对称点B,作点A关于点N的对称点C,连结、、 .(1)、求该抛物线对应的函数表达式;(2)、试说明线段的长度为4;(3)、当直线与抛物线(b是常数)有两个交点时,设这两个交点分别为P、Q(点P在点Q左侧).
①若点M在对称轴左侧,点P在线段上,当此抛物线在内部(包括边)的点的纵坐标最大值与最小值的差为2时,求m的值;
②连结、 , 若点M在对称轴右侧,当时,直接写出m的值.