-
1、合并同类项的结果等于( )A、 B、 C、1 D、
-
2、如图①,在平面直角坐标系中,以点为圆心的圆,交x轴于B,C两点(B在C的左侧),交y轴于A,D两点(A在D的下方) .

【问题提出】
(1)直接写出B、C两点的坐标;
【问题探究】
(2)如图②,将绕点P旋转得到 , 试说明四边形的形状,并求出点M的坐标;
【问题解决】
(3)在一次数学建模设计大赛上,智慧组操作的四个电子机器人A,B,M,C一开始均在如图③所示的上,其中是的直径,四边形是矩形.表演开始后,机器人B先从点B出发,沿直线与直线之间的某个直线方向运动到上的点E处,然后立即调整方向,沿垂直的方向运动到上的点G处停止;机器人M沿直线先运动到的中点Q处,再沿方向运动到点G处和机器人B汇合.请你通过计算分析,机器人M的两次运动路线形成的的大小是否为定值?若是定值,请计算这个定值;若不是定值,请说明理由.
-
3、先化简,再求值: , 其中.
-
4、阅读材料,完成下列任务:
材料一;
材料二:
我们可以用以下方法表示无理数的小数部分.
我们可以用以下方法求无理数的近似值(保留两位小数).
∵ ,
∴ , 即 ,
∴的整数部分为2,
∴的小数部分为 .
∵面积为107的正方形的边长是 , 且 . ∴设 , 其中 , 画出边长为的正方形,如图1:根据图中面积,得 , 当较小时,忽略 , 得 . 解得 .
∴ .

任务:
(1)、利用材料一中的方法,的小数部分是 ;(2)、x是的小数部分,y是的小数部分,则的值是多少?(3)、利用材料二中的方法,探究的近似值(保留两位小数,并写出求解过程) -
5、如图,将平行四边形绕点A旋转得到平行四边形 , 点B'落在边CD上,若 , 当三点共线时,等于 .

-
6、新定义:如果二次函数的图象经过点 , 那么称此二次函数图象为“定点抛物线”.(1)、若抛物线是“定点抛物线”,求该抛物线的表达式.(2)、已知抛物线( , 为常数,且).
①求证:该抛物线为“定点抛物线”;
②若 , 当抛物线的顶点在最低位置时,抛物线上有两点 , , 当时,求的取值范围.
-
7、2025年春节,《哪吒之魔童闹海》(以下简称《哪吒2》)横空出世,现已登顶全球动画电影票房榜,米小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了10名男生和10名女生展开问卷调查(问卷调查满分为100分),并对数据进行整理,描述和分析(评分分数用表示,共分为四组:A:;B:;C:;D: , 下面给出了部分信息:
10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86
20名同学对《哪吒2》评分统计表
性别
平均数
众数
中位数
方差
满分占比
女生
88
a
90
112.2
10%
男生
88
100
b
200.2
50%

根据以上信息,解答下列问题:
(1)、上述图表中的______________________,___________(2)、根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;(写出一条理由即可)(3)、我校初三年级有500名女生和600名男生去看过《哪吒2》,估计这些学生中对《哪吒2》的评分在D组共有多少人? -
8、解方程: .
-
9、先化简,再求值: , 其中 .
-
10、已知一组数据的平均数为4,方差是 , 则另一组数据的平均数和方差分别是( )A、4,5.2 B、8,6.4 C、10,12.8 D、12,16
-
11、在一条笔直的公路上A、B两地相120km,甲车从A地开往B地,乙车从B地开往A地,甲比乙先出发.设甲、乙两车距A地的路程为y千米,甲车行驶的时间为x小时,y与x之间的关系如图所示,下列说法错误的是( )
 A、甲车的速度比乙的速度慢 B、甲车出发1小时后乙才出发 C、甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D、乙车达到A地时,甲车离A地90km
A、甲车的速度比乙的速度慢 B、甲车出发1小时后乙才出发 C、甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D、乙车达到A地时,甲车离A地90km -
12、《孙子算经》下卷第28题译成现代文意思是:现有甲乙二人,身边各有多少钱,不清楚.如果甲的钱数加上乙的钱数的一半,钱数一共是48;如果乙的线数加上甲的钱数的 , 钱数一共也是48.问甲乙二人各有多少钱?( )A、24,36 B、36,18 C、36,24 D、24,18
-
13、如图,已知 , 是正方形的对角线上的两点, , , 则四边形的周长是( )
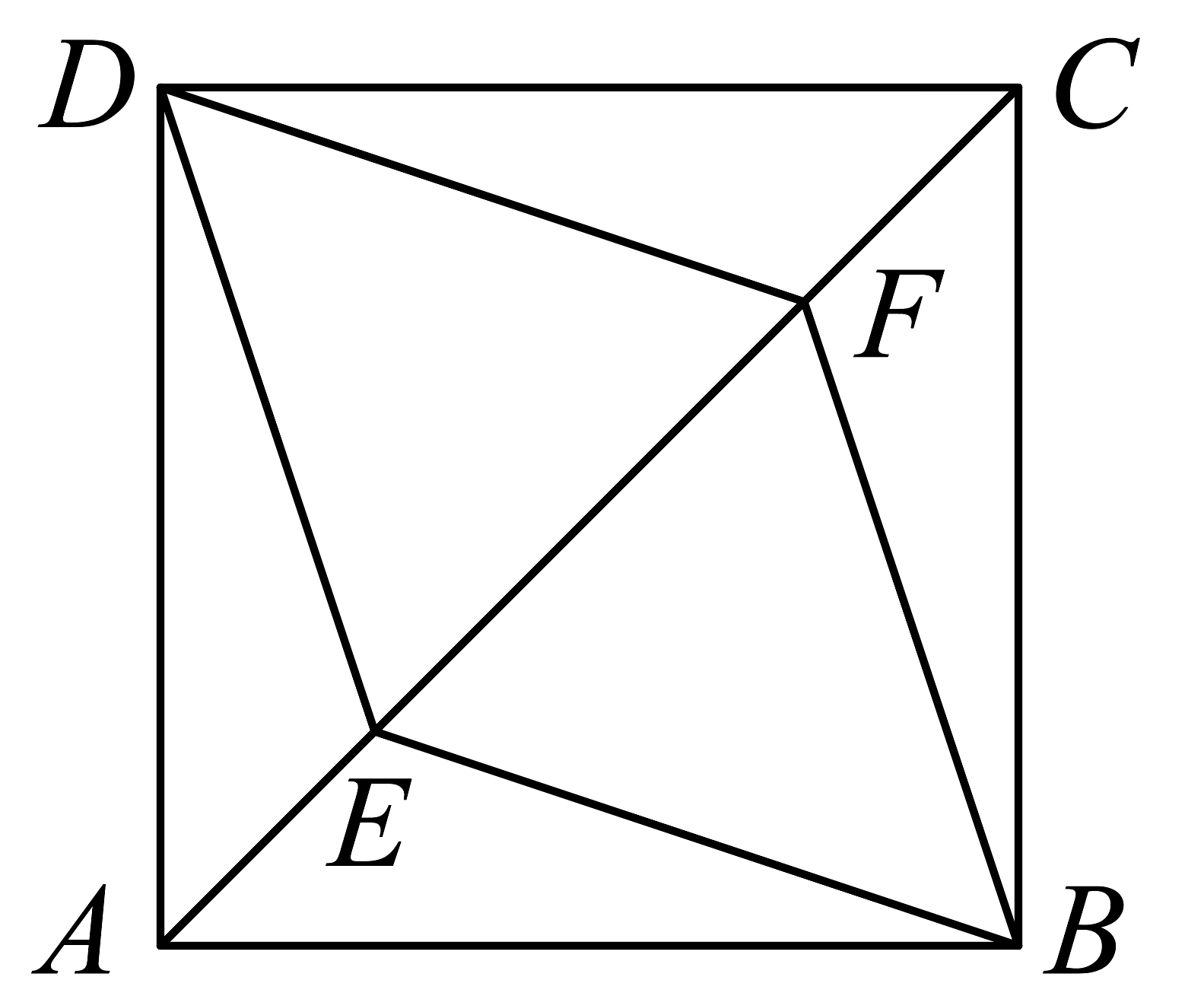 A、8 B、 C、 D、4
A、8 B、 C、 D、4 -
14、2025年春节假期,兰州市旅游收入约42亿元,将42亿用科学记数法表示为( )A、 B、 C、 D、
-
15、观察如图所示的三种视图,与之对应的物体是( )
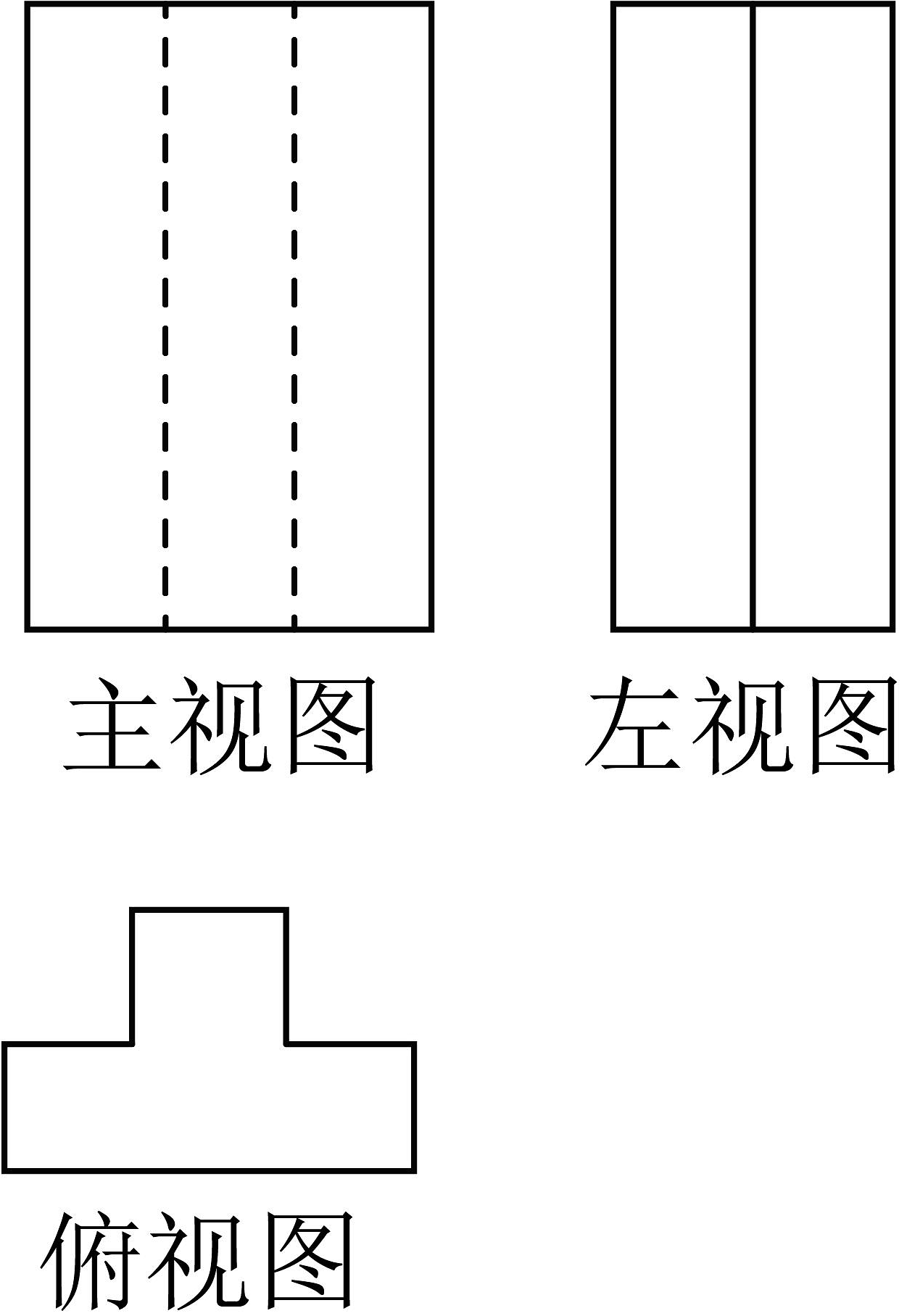 A、
A、 B、
B、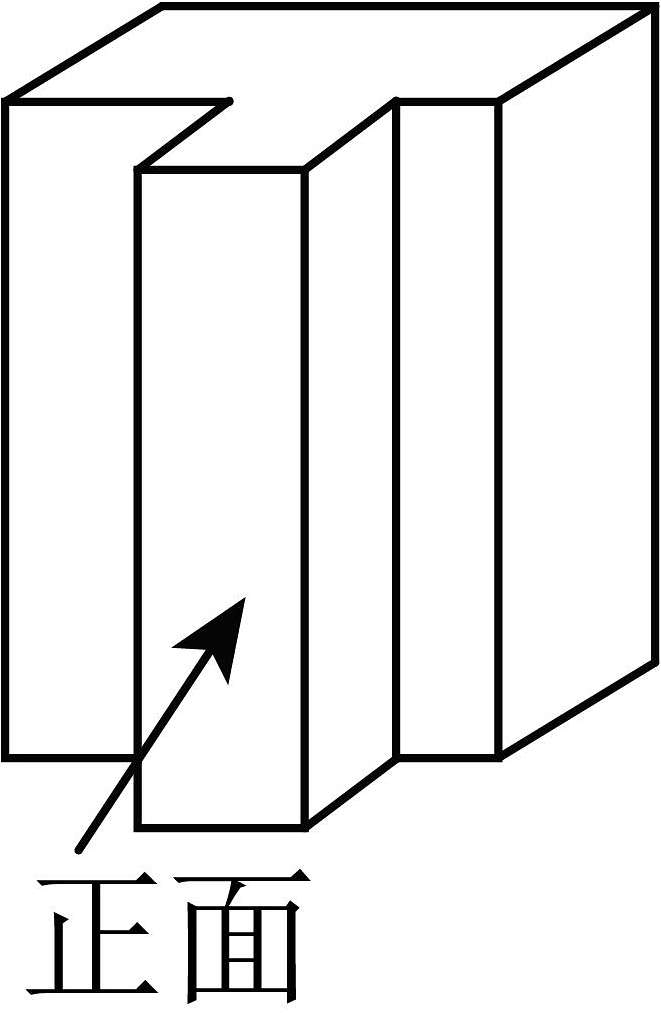 C、
C、 D、
D、
-
16、【问题提出】小丽在上自主学习时,看到一个结论:对于任何一个封闭的平面图形,存在一条直线既平分周长,又平分面积.于是小丽利用初中所学知识进行初步验证.
【问题探究】
(1)小丽先选择了几个特殊图形进行验证,如图,请你在三个图形中任选两个,分别作一条直线,使这条直线既平分你所选图形的周长,又平分它的面积;
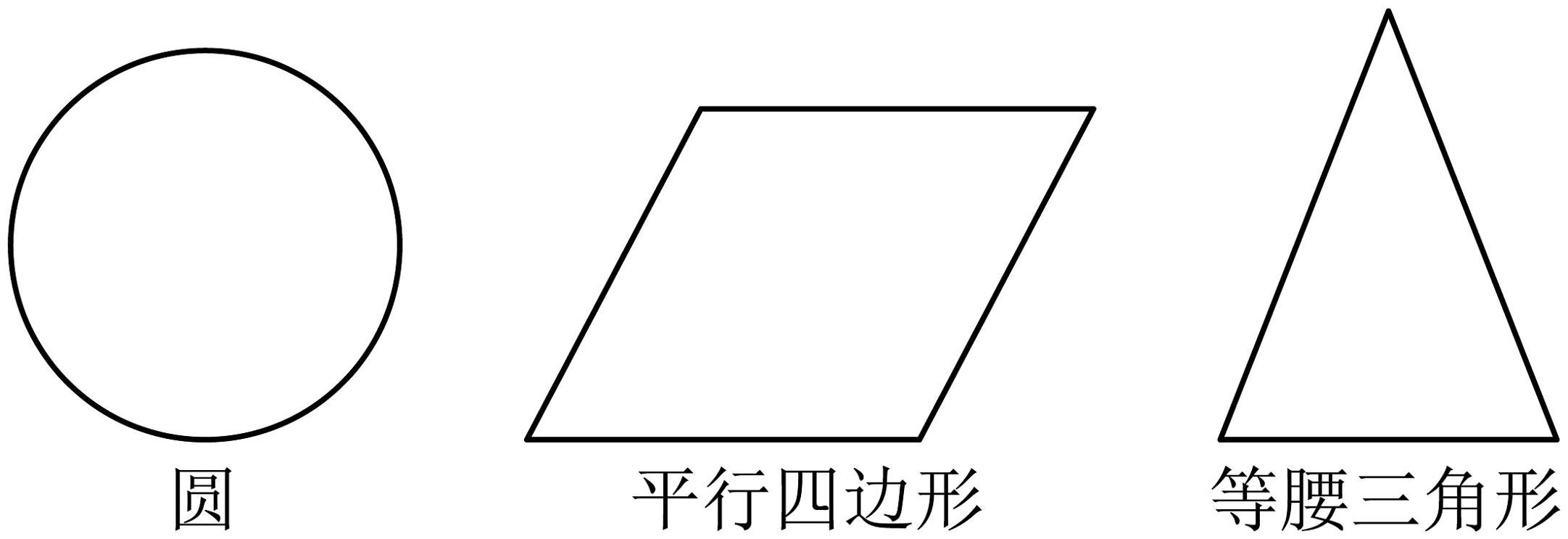
(2)如图,小丽在直角三角形中,作出一条直线 , 交于点E、交于点F,直线既平分的周长,又平分的面积.请根据小丽所给的数据计算:若 , , , , 用含有a的代数式表示 , 并求a的值;
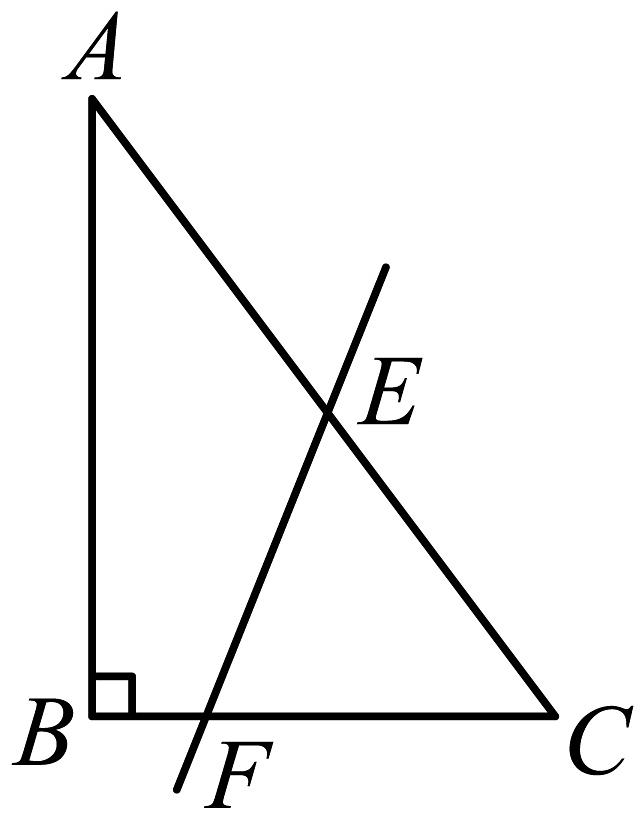
【问题解决】
(3)小丽家所在小区平面示意图如图,小区为方便居民出行,准备修一条笔直的道路(路宽不计),使这条道路所在的直线既平分四边形的周长,又平分四边形的面积.小丽利用所学知识进行思考,通过测量示意图得到 , , , , , . 若该道路的一个出口在边上,请帮小丽在图中画出这条直线,并在图中标出所有线段的长度.

-
17、某校为学生拍毕业照设计了一个拱门,该拱门的横截面由线段和一段抛物线构成,垂直于地面.将其截面放入平面直角坐标系如图1所示,点O为坐标原点,已知 , 抛物线顶点E的坐标为 .
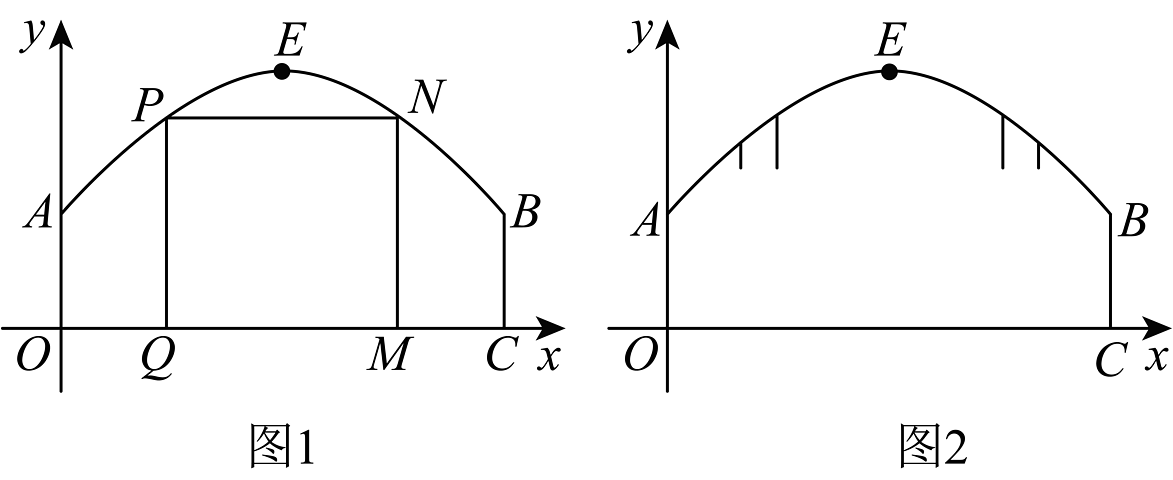 (1)、求拱门抛物线的函数关系式;(2)、现要在抛物线与地面围成的区域中用 , , 三根钢架隔出正方形区域供师生拍照留念,点P,N在抛物线上,点Q,M在地面上,求此正方形的边长;(3)、如图2,在拱门上安装彩灯,要求彩灯到地面的垂直距离为 , 每两个相邻彩灯之间的水平距离相等且不超过 , 左右外侧的两个彩灯安装在拱门的抛物线上.求至少需要安装彩灯的个数.(参考数据:)
(1)、求拱门抛物线的函数关系式;(2)、现要在抛物线与地面围成的区域中用 , , 三根钢架隔出正方形区域供师生拍照留念,点P,N在抛物线上,点Q,M在地面上,求此正方形的边长;(3)、如图2,在拱门上安装彩灯,要求彩灯到地面的垂直距离为 , 每两个相邻彩灯之间的水平距离相等且不超过 , 左右外侧的两个彩灯安装在拱门的抛物线上.求至少需要安装彩灯的个数.(参考数据:) -
18、如图,已知内接于 , 直径平分∠ACB,交于点D,交于点E,连接 .
 (1)、填空: (选填“<”、“>”或“=”);(2)、用尺规在图中作直线 , 使得直线与相切于点C;(保留作图痕迹,不写作法)(3)、判断与的位置关系,并说明理由.
(1)、填空: (选填“<”、“>”或“=”);(2)、用尺规在图中作直线 , 使得直线与相切于点C;(保留作图痕迹,不写作法)(3)、判断与的位置关系,并说明理由. -
19、沿河土家族自治县位于乌江下游,被称为“乌江百里画廊”.某数学兴趣小组借助无人机测量乌江某段河道的宽度.如图,在河岸边的点C处,兴趣小组控制一架无人机沿倾斜角的方向飞行到达点A处,然后无人机又沿垂直于河道的方向水平飞行至点B处,此时测得河对岸D处的倾斜角为 , 图中点A,B,D,C在同一平面内.
 (1)、求无人机从C飞到A时垂直上升的距离(结果保留根号);(2)、求该段河道的宽度(结果保留整数).(参考数据: , , , )
(1)、求无人机从C飞到A时垂直上升的距离(结果保留根号);(2)、求该段河道的宽度(结果保留整数).(参考数据: , , , ) -
20、贵州玉屏县被誉为“箫笛之乡”.玉屏县某中学举办“箫笛艺术节”活动,现需购买玉箫、玉笛若干支.已知玉萧单价比玉笛单价高10元,用1000元购买的玉萧数量与800元购买的玉笛数量相同.(1)、求玉萧和玉笛的单价各是多少元?(2)、学校计划购买玉箫与玉笛共30支,且玉箫的数量不少于玉笛数量的2倍,则学校最少需花费多少元?