相关试卷

1、计算：

(1)、 $3 \sqrt{2} - |\sqrt{3} - \sqrt{2}|$

(2)、 $- 1^{2022} + \sqrt{16} \times {(- 3)}^{2} + (- 6) \div \sqrt[3]{- 8}$

查看解析
2、已知关于 $x, y$ 的方程组 $\{\begin{cases} x + y = m + 2 \\ 2 x - 5 y = 3 \end{cases}$ 的解满足 $x - 2 y > 1$ ，则 $m$ 的取值范围为．

查看解析
3、某校为了了解八年级学生身高的范围和整体分布情况，抽样调查了八年级50名学生的身高，其中身高最高的是 $17 6cm$ ，最矮的是 $147 cm$ ，若以 $5 cm$ 为组距，应把这些数据分成组．

查看解析
4、如图，直线 $A B$ 和 $C D$ 交于O点， $O D$ 平分 $∠ B O F ， O E ⊥ C D$ 于点 $O ， ∠ A O C = 30 °$ ，则 $∠ E O F =$ ．

查看解析
5、已知直线 $A B ∥ C D$ ，点P在直线 $A B ， C D$ 之间，连接 $A P ， C P$ ．
下面结论正确的个数为（）
①如图1，若 $∠ A P C = α$ ， $∠ P A B = β$ ，则 $∠ P C D = 360 ° - α - β ；$
②如图2，点Q在 $A B ， C D$ 之间， $∠ Q A P = 2 ∠ Q A B ， ∠ Q C P = 2 ∠ Q C D$ ，则 $∠ A P C + 3 ∠ A Q C = 360 °$ ；
③如图3， $∠ P A B$ 的角平分线交CD于点M，且 $A M ∥ P C$ ，点N在直线 $A B ， C D$ 之间，连接 $C N ， M N$ ， $∠ P C N = n ∠ N C D ， ∠ A M N = \frac{1}{n} ∠ N M D ， n > 1$ ，则 $∠ P$ 和 $∠ N$ 的关系为 $\frac{∠ N}{∠ P} = \frac{n + 1}{n - 1}$ （用含n的式子表示，题中的角均指大于 $0 °$ 且小于 $180 °$ 的角）．

A、0 B、1 C、2 D、3

查看解析
6、若关于x的不等式组 $\{\begin{matrix} \frac{3 x + 5}{2} - 5 > \frac{5}{2} - x \\ 3 x - 2 a \geq 5 x + 4 \end{matrix}$ 恰有3个整数解，则a的取值范围是（）

A、 $5 \leq a < 6$ B、 $5 < a \leq 6$ C、 $- 8 \leq a < - 7$ D、 $- 8 < a \leq - 7$

查看解析
7、甲骨文是中华优秀传统文化的根脉．下列甲骨文中，能用其中一部分平移得到的是（）

A、 B、 C、 D、

查看解析
8、如图1，抛物线 $y = a x^{2} + b x - 2 (a \neq 0)$ 与y轴交于点A，与x轴交于点 $B (- \frac{1}{2}, 0)$ 、 $C (4, 0)$ ，点P是直线 $A C$ 下方抛物线上一动点，分别连接 $A C, A P, C P$ ．

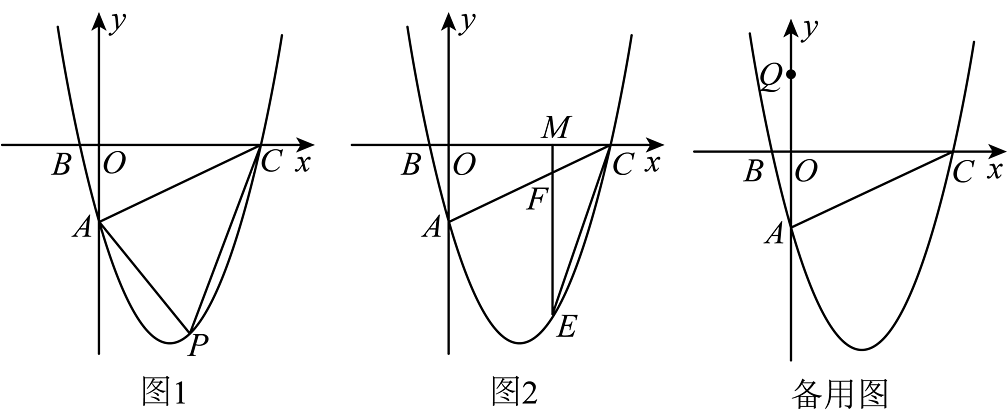(1)、求抛物线表达式；

(2)、当 $△ P A C$ 的面积是 $△ O A C$ 面积的2倍时，求点P的坐标；

(3)、将线段 $A C$ 沿x轴的负方向平移得到 $A^{'} C^{'}$ ，点A的对应点为点 $A^{'}$ ，点C的对应点为点 $C^{'}$ ，点Q为点A关于x轴的对称点，连接 $Q A^{'} 、 Q C^{'}$ ，在线段平移过程中，求 $Q A^{'} + Q C^{'}$ 的最小值．

查看解析
9、如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 交 $B C$ 于点 $D$ ，过点 $D$ 作 $D E ⊥ A C$ ，垂足为 $E$ ，交 $B A$ 的延长线于点 $F$ ．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $A F = 2$ ， $\tan ∠ F = \frac{3}{4}$ ，求 $⊙ O$ 的半径．

查看解析
10、广西水果全国产量第一，而蓬勃发展的快递业，为广西的新鲜水果及时走进千家万户提供了极大便利．不同的快递公司在配送、服务、收费和投递范围等方面各具优势．火龙果种植户小丽经过初步了解，打算从甲、乙两家快递公司中选择一家合作，为此，小丽收集了10家火龙果种植户对两家公司的相关评价，并整理、描述、分析如下：
a．配送速度得分：
甲：6、6、7、7、7、8、9、9、9、10
乙：6、7、7、8、8、8、8、9、9、10
c．配送速度和服务质量得分统计表：
统计量快递公司
配送速度得分
服务质量得分
平均数
中位数
平均数
方差
甲
$7.8$
m
7
$S_{甲}^{2}$
乙
8
8
7
$S_{乙}^{2}$
b．服务质量得分统计图：

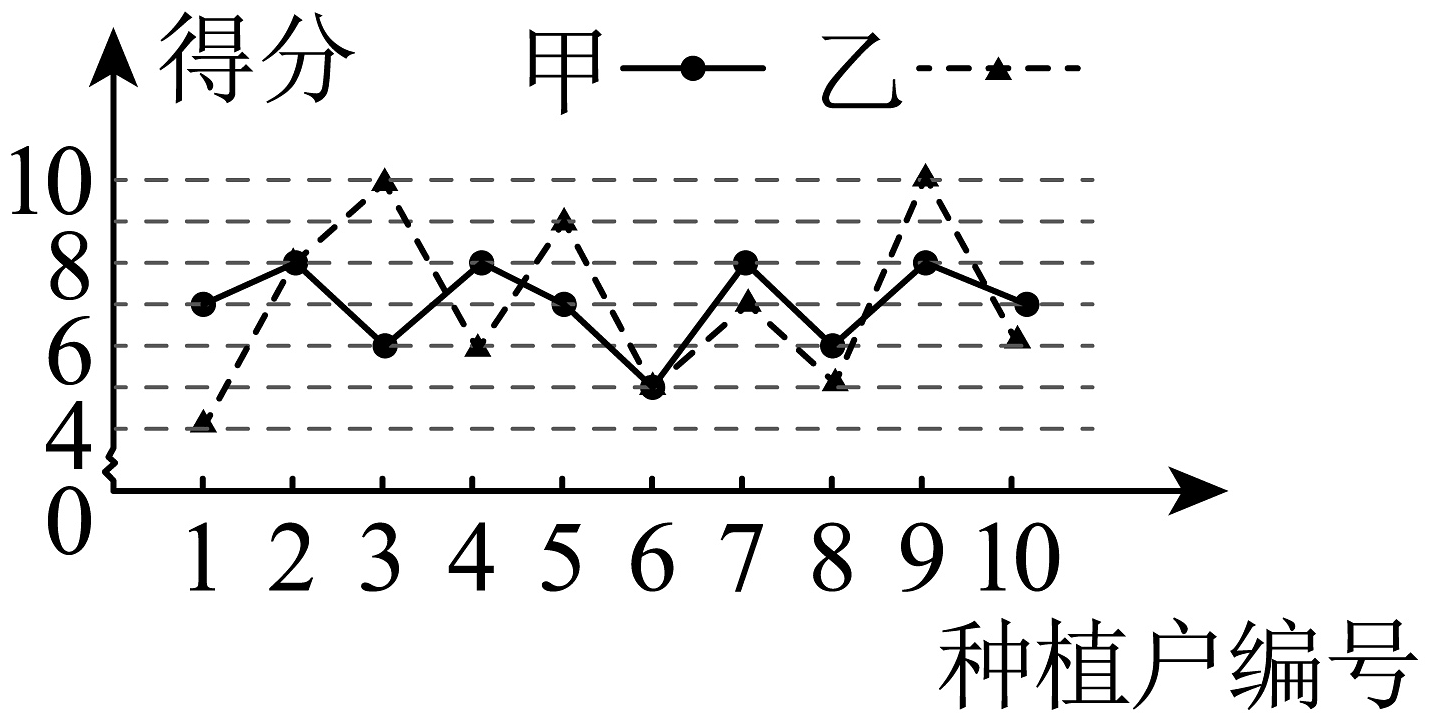
根据以上信息，回答下列问题：

(1)、表格中的 $m =$ ； $S_{甲}^{2}$ $S_{乙}^{2}$ （填“ $>$ ”“=”或“ $<$ ”)．

(2)、综合上表中的统计量，你认为小丽应选择哪家公司？请说明理由．

查看解析
11、在中国古代，数学被称为“算术”或“九章之学”，而几何知识常用于天文、测地、建筑、乃至器物制作中．古人用“矩”、“规”巧妙地构建出各类精妙图形．在这样的背景下，匠人们常以尺规作图解决实际问题，体现“法天则地”的智慧精神．
如今，借助尺规来完成一道几何构造题：
如图，已知： $△ A B C$ ，尺规作图得四边形 $D B E C$ ．作图步骤如下：
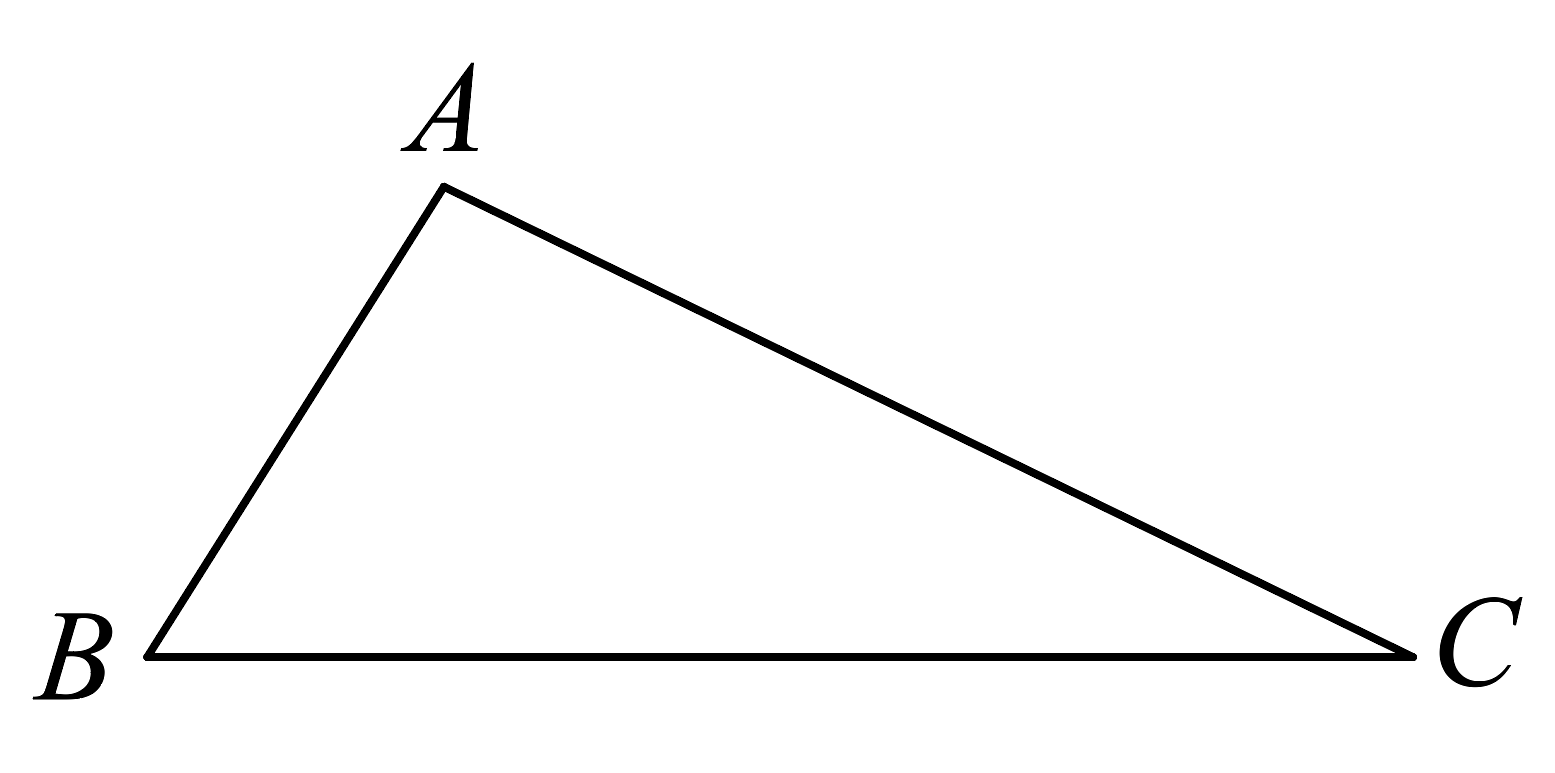
①分别以B、C为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两条弧分别相交于点P，Q；
②作直线 $P Q$ 交 $A C$ 于点D，连接 $B D$ ；
③以B为圆心， $B D$ 的长为半径作弧，交直线 $P Q$ 于点E，连接 $C E, B E$ ．

(1)、请用上面方法，用没有刻度的直尺和圆规作出四边形 $D B E C$ ．（不写作法，保留作图痕迹）；

(2)、若 $∠ B A C = 90 °$ ， $A B = 8 cm, A C = 16 cm$ ，则四边形 $D B E C$ 的面积是__________ $cm$ ．

查看解析
12、先化简，再求值： $(\frac{a}{a - 1} - 1) \div \frac{a^{2} + a}{a^{2} - 1}$ ，其中 $a = \frac{5}{2}$ ．

查看解析
13、解不等式组： $\{\begin{cases} 2 (x - 2) < x - 3 ① \\ x > \frac{3 x - 2}{4} ② \end{cases}$ ．

查看解析
14、计算： $\sqrt{2} (\sqrt{3} + \sqrt{2}) - \sqrt{8} \div \sqrt{2}$ ．

查看解析
15、如图，水池中心点O处竖直安装一水管，水管喷头喷出抛物线形水柱，喷头上下移动时，抛物线形水柱随之竖直上下平移，水柱落点与点O在同一水平面．安装师傅调试发现，喷头高 $2 .5m$ 时，水柱落点距O点 $2 .5m$ ；喷头高 $4m$ 时，水柱落点距O点 $3m$ ．那么喷头高m时，水柱落点距离O点 $2m$ ．

查看解析
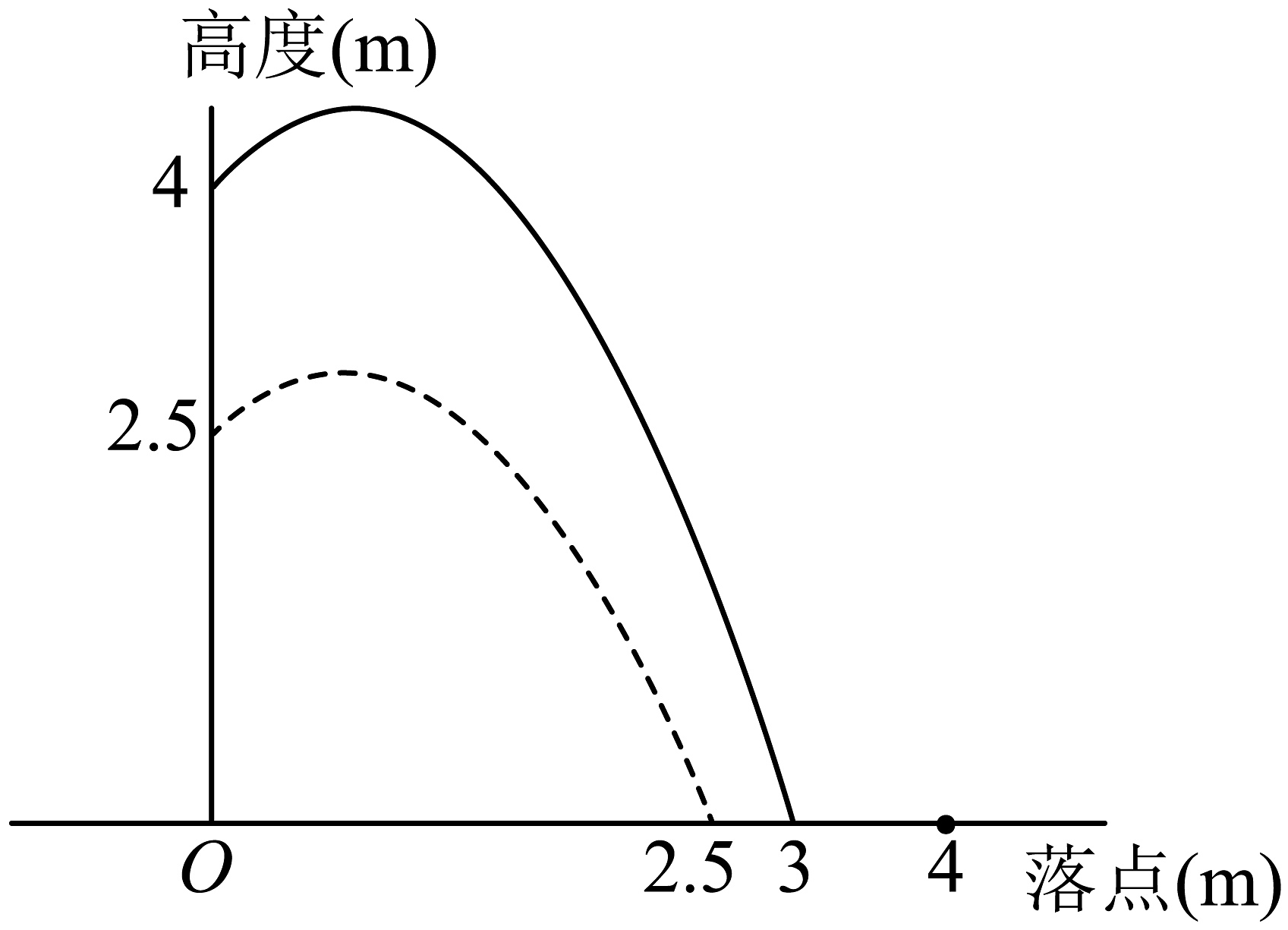
16、关于 $x$ 的一元二次方程 $x^{2} + 3 x + 2 c = 0$ 有两个不相等的实数根，则 $c$ = ．（写出一个满足条件的值）

查看解析
17、如图，一束平行于主光轴的光线 $A B$ 经凸透镜折射后，其折射光线 $B F$ 与一束经过光心O的光线 $C D$ 相交于点P，点F为凸透镜的焦点．若 $∠ A B F = 145 °$ ， $∠ C O E = 30 °$ ，则 $∠ D P F$ 的度数为（）

A、 $45 °$ B、 $55 °$ C、 $65 °$ D、 $75 °$

查看解析
18、随着人工智能技术的不断突破，人形机器人行业备受关注，未来行业将持续保持高速发展．如图是某机构对2025～2030年全球人形机器人市场规模预测的数据：
根据预测数据，下列分析正确的是（）
①2025～2030年全球人形机器人市场规模逐年增长；
②2025～2030年全球人形机器人市场规模增长率逐年增大；
③2025～2030年全球人形机器人市场总规模超7000亿元；
④若保持与2030年相同的年增长率，到2032年全球人形机器人市场规模将超万亿元．

A、①④ B、①② C、②③④ D、①②④

查看解析
19、截至4月12日17时38分，电影《哪吒之魔童闹海》全球总票房达到156.29亿元，也是我国首部百亿电影．将数据“156.29亿”用科学记数法表示为（）

A、 $156.29 \times 10^{8}$ B、 $15.629 \times 10^{10}$ C、 $1.5629 \times 10^{10}$ D、 $0.15629 \times 10^{9}$

查看解析
20、下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = a^{9}$ B、 $2 a^{3} \div a^{2} = a$ C、 ${(- a^{2})}^{2} = a^{4}$ D、 $a^{4} + a^{2} = a^{6}$

查看解析

上一页 915 916 917 918 919 下一页跳转

统计量快递公司	配送速度得分		服务质量得分
统计量快递公司	平均数	中位数	平均数	方差
甲	$7.8$	m	7	$S_{甲}^{2}$
乙	8	8	7	$S_{乙}^{2}$