-
1、有着冰上“国际象棋”之称的冰壶如图放置时,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
2、下列四个数中最小的是( )A、 B、 C、0 D、5
-
3、篮球跃动身心,健康点亮生活.小星在距离篮筐7米处投篮,准确命中篮筐,篮球出手时离地的高度为米.已知篮筐中心离地面3米,篮球飞行的轨迹是一条抛物线,且在距离出手点水平方向4米处达到最高点4米.小星同学学习了二次函数之后,建立了如图2所示的直角坐标系,其中出手点的坐标为 , 篮筐点的坐标为 , 并求出球的高度关于水平方向运动的距离的二次函数表达式为 .
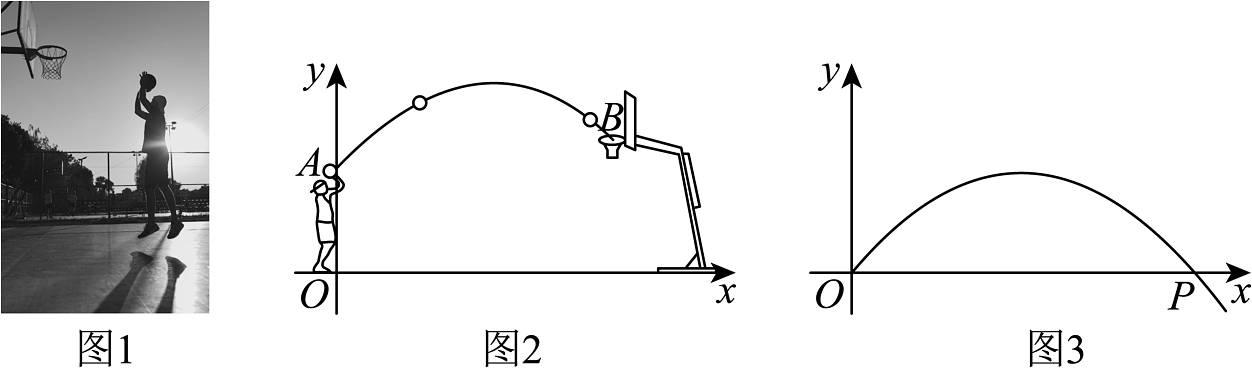 (1)、的值为______;的值为______;(2)、若在小星将球投出手的同时,防守球员小明立即跑位到小星的正前方进行回防,已知小明起跳时手心离地的最大高度为米.请问小明能否成功将正在空中飞行的球拦截?若能,请说明理由,并求出拦截成功时小明距离小星出手点时的水平距离;(3)、如图3,小星同学进一步研究所得到的二次函数的图象性质,他对原二次函数进行优化,使得自变量的取值范围为 , 并将原二次函数的图象向下平移个单位,得到一个新的二次函数: , 新函数图象与轴交于点 . 点在对称轴右侧的抛物线上,点N在轴上,点在其对称轴上,且到轴的距离为1,并且点位于第一象限,请问是否存在以点F、P、M、N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
(1)、的值为______;的值为______;(2)、若在小星将球投出手的同时,防守球员小明立即跑位到小星的正前方进行回防,已知小明起跳时手心离地的最大高度为米.请问小明能否成功将正在空中飞行的球拦截?若能,请说明理由,并求出拦截成功时小明距离小星出手点时的水平距离;(3)、如图3,小星同学进一步研究所得到的二次函数的图象性质,他对原二次函数进行优化,使得自变量的取值范围为 , 并将原二次函数的图象向下平移个单位,得到一个新的二次函数: , 新函数图象与轴交于点 . 点在对称轴右侧的抛物线上,点N在轴上,点在其对称轴上,且到轴的距离为1,并且点位于第一象限,请问是否存在以点F、P、M、N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由. -
4、如图,在四边形中, , 且 , 以B为端点,作射线 , 在射线上截切 , 并分别连接 , 其中分别交于点F和点G.
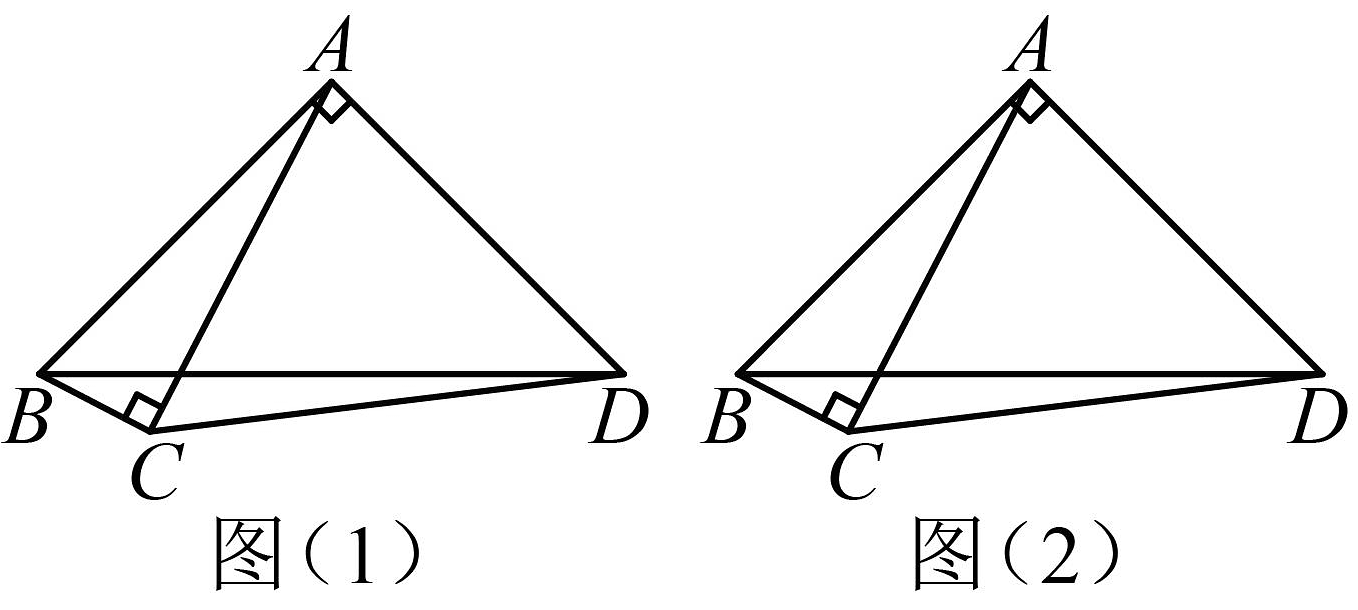 (1)、【动手操作】根据题意请在图(1)中补全图形;(2)、【问题探究】求证:;(3)、【拓展延伸】若 , 求的长,并说明理由.
(1)、【动手操作】根据题意请在图(1)中补全图形;(2)、【问题探究】求证:;(3)、【拓展延伸】若 , 求的长,并说明理由. -
5、如图,已知是的直径,为上一点,的角平分线交于点D,F在直线上,且 , 垂足为 , 连接 .
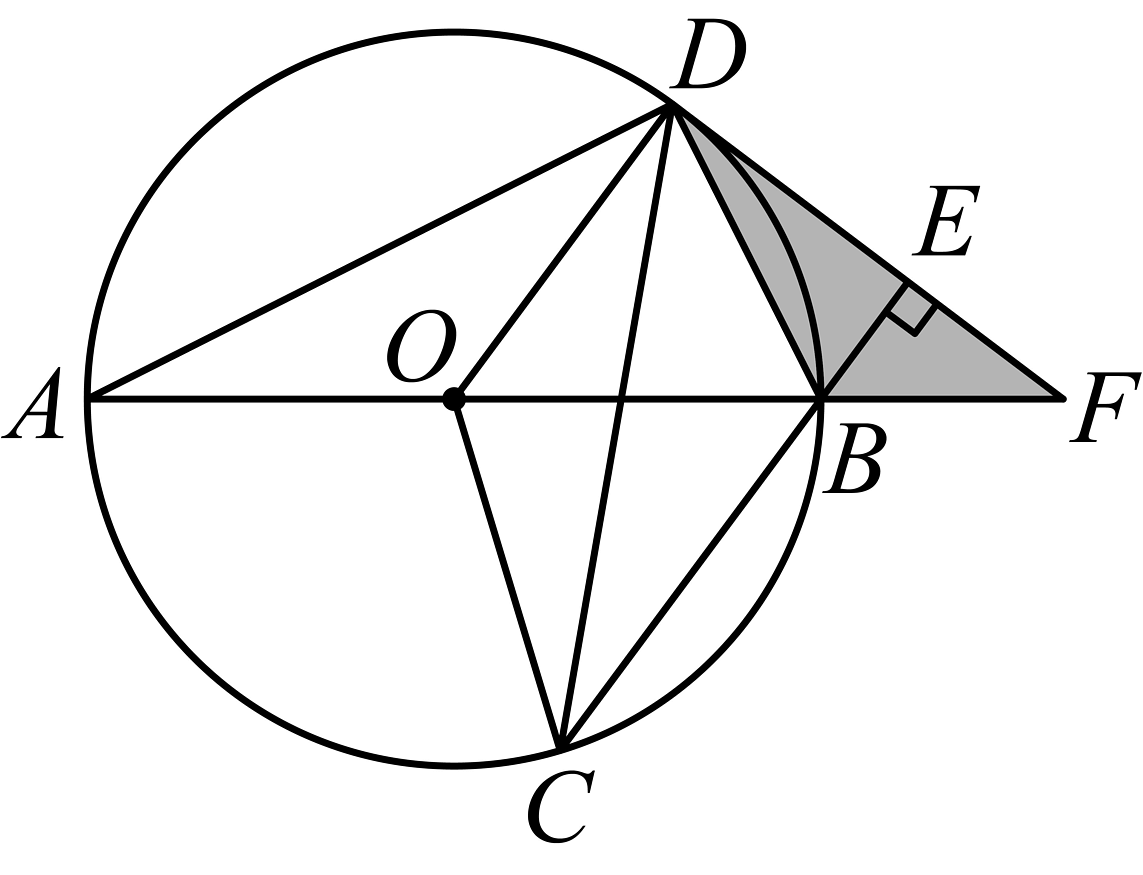 (1)、请写出一个与相等的角:______;(2)、求证:是的切线;(3)、若 , 的半径为6,求图中阴影部分的面积.
(1)、请写出一个与相等的角:______;(2)、求证:是的切线;(3)、若 , 的半径为6,求图中阴影部分的面积. -
6、根据如下素材,探索完成任务.
解决如何确定图书销售单价及怎样进货以获取最大利润问题.
条件一:某书店为了迎接“读书节”决定购进A,B两种新书,两种图书的进价分别是每本18元、每本12元)
条件二:已知A种图书的标价是B种图书标价的1.5倍,若顾客用600元按标价购买图书,能单独购买A种图书的数量恰好比单独购买B种图书的数量少10本.
条件三:该书店准备用不超过16800元购进A,B两种图书共1000本,且A种图书不少于700本经市场调查后调整销售方案为:A种图书按照标价的8折销售,B种图书按标价销售.
任务解决:
(1)、探求图书的标价,请运用适当方法,求出两种图书的标价;(2)、确定如何获得最大利润,书店应怎样进货才能获得最大利润,最大利润是多少? -
7、如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点是正方形与反比例函数图象的一个交点,点是正方形与正半轴的交点.已知点在该反比例函数的图象上.
 (1)、求这个反比例函数的表达式;(2)、若 , 求图中阴影部分的面积.
(1)、求这个反比例函数的表达式;(2)、若 , 求图中阴影部分的面积. -
8、根据以下信息,探索完成任务.
如何设计窗户限位器位置
信息1
问题背景
平开窗是生活中常见的一种窗户,安装平开窗需要一种滑撑支架,如图是这种平开窗的实物展示图.


信息2
数学抽象
把平开窗的滑撑支架抽象成如下示意图.已知滑撑支架的滑动轨道固定在窗框底边,固定在窗页底边,点B,C,D三点固定在同一直线上.当窗户关闭时,点与点重合,和均落在上;当点向点滑动时,四边形始终为平行四边形,其中 , .
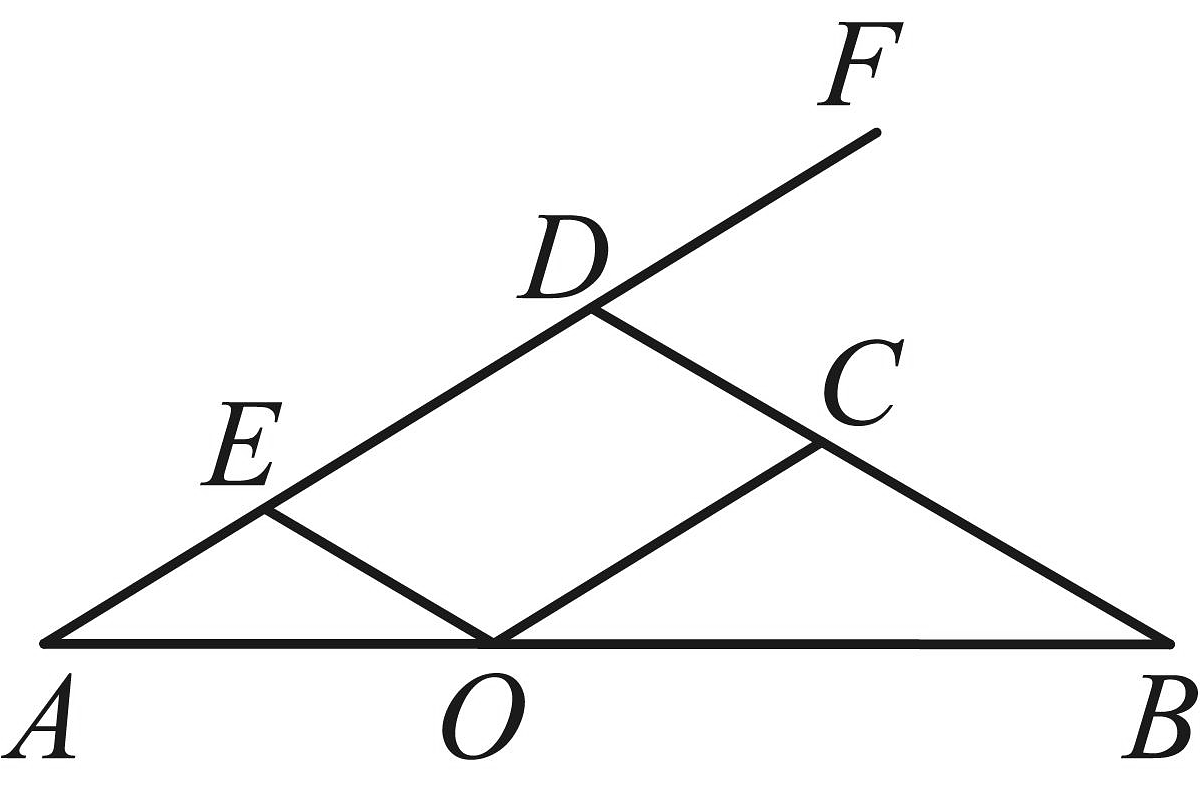
信息3
安全规范
窗户打开一定角度后,与形成一个角 . 出于安全考虑,部分公共场合的平开窗有开启角度限制要求:平开窗的开启角度应该控制在以内(即).
问题解决
任务1
求解关键数量
滑撑支架中的长度为______ , 滑动轨道的长度是______ .
任务2
确定安装方案
为符合安全规范要求,某公共场合的平开窗需在滑动轨道上安装一个限位器 , 控制平开窗的开启角度,当点滑动到点时 , 则限位器应装在离点多远的位置?(结果精确到0.1)
参考数据:)
-
9、某中学开展“阳光体育”运动,根据实际情况,决定开设篮球、健美操、跳绳、毽球四个运动项目,为了解学生最喜爱哪一个运动项目,学校从不同年级随机抽取部分学生进行调查,每人必须选择且只能选择一个项目,并将调查结果绘制成如图所示两幅统计图.请根据图中提供的信息,解答学生喜欢运动项目的下列问题:
 (1)、本次调查的学生共有______人;并把条形统计图补充完整;(2)、在最喜爱健美操项目的学生中,九(一)班有2名同学和九(二)班有2名同学有健美操基础,学校准备从这4人中随机抽取2人作为健美操领操员,请用列表或画树状图的方法求选中的2名同学恰好是同一个班级的概率.
(1)、本次调查的学生共有______人;并把条形统计图补充完整;(2)、在最喜爱健美操项目的学生中,九(一)班有2名同学和九(二)班有2名同学有健美操基础,学校准备从这4人中随机抽取2人作为健美操领操员,请用列表或画树状图的方法求选中的2名同学恰好是同一个班级的概率. -
10、(1)计算:
(2)请从下列三个方程中任选两个组成一个方程组,并求解该方程组.
①;②;③
-
11、如图,在正方形中,是边上靠近的三等分点,是的中点,是对角线上的动点,当取得最小值时,的值是 .

-
12、如图是用棋子摆成的“小房子”,按照这样的规律,摆第8个图形需要枚棋子.

-
13、一个袋中装有5个红球、3个白球和2个黄球,每个球除颜色外都相同,小明从中任意摸出一个球,则摸到白球的概率为 .
-
14、化简: .
-
15、二次函数的部分图象如图所示,其对称轴为直线 , 且与x轴的一个交点坐标为 . 下列结论错误的是( )
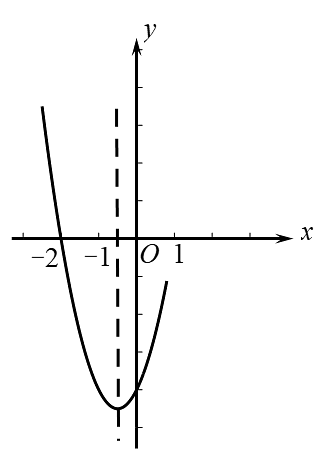 A、抛物线与x轴的另一个交点坐标是 B、当时,y随x的增大而增大 C、的值是0 D、
A、抛物线与x轴的另一个交点坐标是 B、当时,y随x的增大而增大 C、的值是0 D、 -
16、如图,的半径为 , 点、、都在上, , 则弧的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为( )
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
18、如图,小手盖住的点的坐标可能为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、用不等式表示图中的解集,下列正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、学校准备准备购买一款校服,对全校同学喜欢的颜色进行了问卷调查,统计结果如表所示:
颜色
白色
红色
蓝色
学生人数
100
820
180
学校最终决定购买红色校服,其参考的统计量是( )
A、平均数 B、中位数 C、众数 D、方差