-
1、下列各数中与相加,和最小的是( )A、 B、2 C、0 D、1
-
2、在菱形中,点为射线(不与点重合)上一动点,连接 , 点为中点,连接 , 将沿翻折得到 , 连接 .
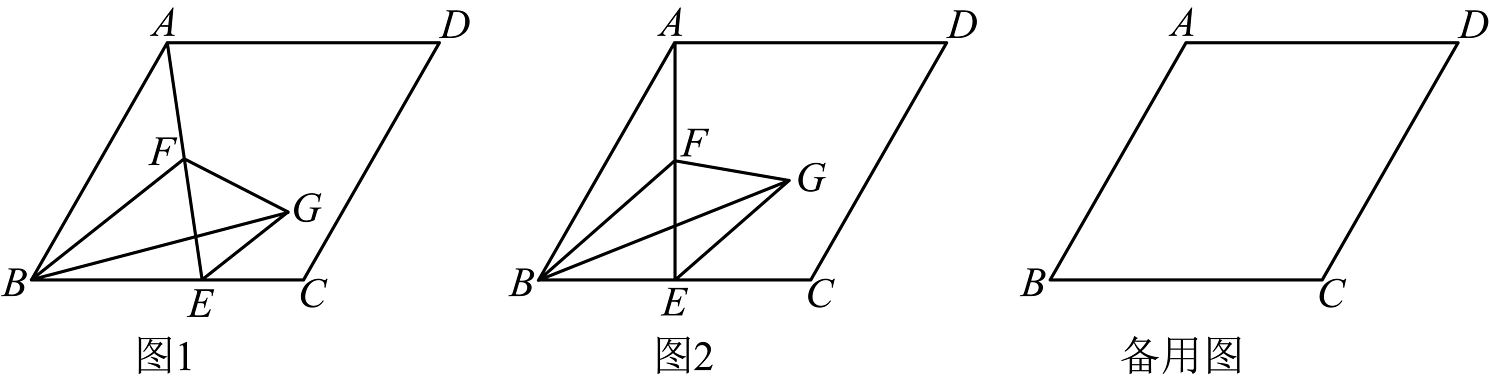 (1)、如图1,连接 , 与的位置关系是_______________;与的位置关系是_____________;(2)、如图2,若 , 当点运动到中点时,求的值;(3)、已知 , , 若 , 则的长为_____________.
(1)、如图1,连接 , 与的位置关系是_______________;与的位置关系是_____________;(2)、如图2,若 , 当点运动到中点时,求的值;(3)、已知 , , 若 , 则的长为_____________. -
3、综合与实践
深圳自然博物馆位于广东省深圳市坪山区燕子湖片区,共划分为陈列展览区、藏品保管保护区、公共服务区、科普教育区、综合业务与学术研究区以及地下车库和设备用房六大功能部分,是深圳市“新时代十大文化设施”之一,建成后将成为粤港澳大湾区首座大型综合类自然博物馆,填补了该区在综合类自然博物馆方面的空白.坪山区某中学数学兴趣小组对该项目设计图进行了研究:
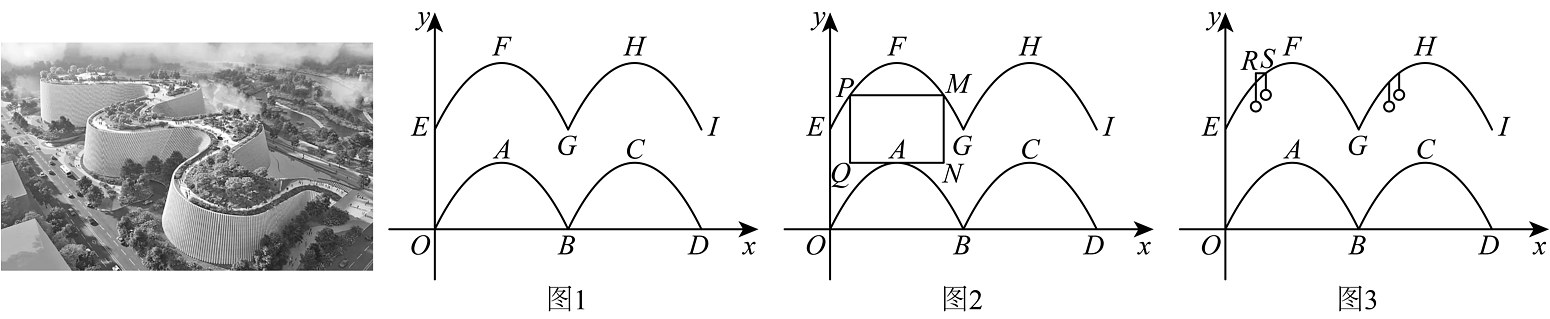
把建筑俯视图的一部分抽象为以下图象:曲线、曲线、曲线和曲线 , 它们均可以看成某二次函数图象的一部分,后三者都可以看成由曲线平移得到,的长度为6.如图1,兴趣小组建立平面直角坐标系,已知曲线最高点点坐标为 .
(1)、求曲线所在抛物线的解析式(不需要写自变量的取值范围).(2)、如图2,现在需要在建筑的顶部划出一片矩形区域来做绿化,下图所示,其中轴,求矩形花园周长的最大值.(3)、如图3,为了增强建筑物晚上的整体美观度,如果在建筑的曲线和曲线的外墙上安装具备灯光效果的垂直灯具,假设每个垂直灯具的水平间距为0.6,即 , 请问至少需要安装垂直灯具____________个. -
4、如图,在中, , , .
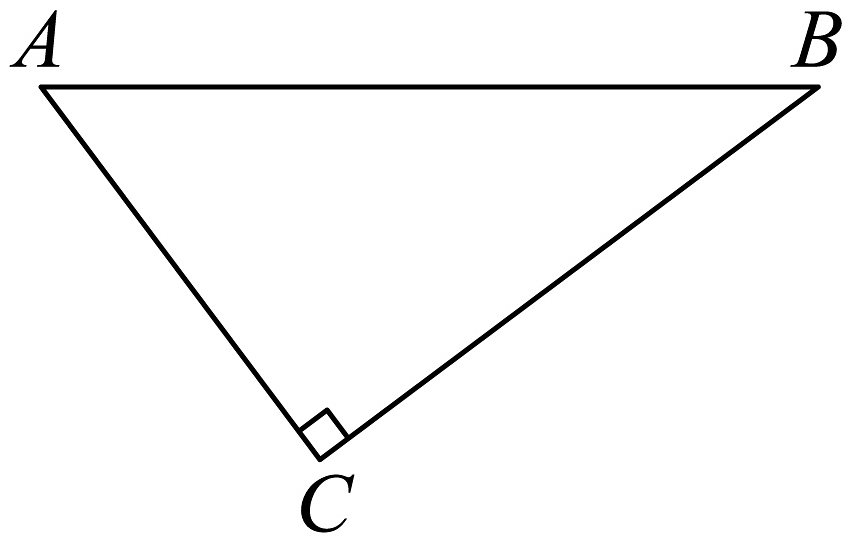 (1)、请用圆规和没有刻度的直尺作出 , 使圆心在边上,且与 , 两边都相切;(保留作图痕迹,不写作法和证明)(2)、在(1)的条件下,求的半径长.
(1)、请用圆规和没有刻度的直尺作出 , 使圆心在边上,且与 , 两边都相切;(保留作图痕迹,不写作法和证明)(2)、在(1)的条件下,求的半径长. -
5、坪山大剧院位于坪山文化聚落,是一个戏剧文化的综合空间、一个先锋戏剧的原创基地、一个品质引领的文化地标.为了加深对于戏剧文化的了解,小坪同学和小山同学准备组织一次到坪山大剧院的观剧活动.他们对同班同学发放了调查问卷,统计同学们最喜欢的戏剧种类,其调查结果如下:
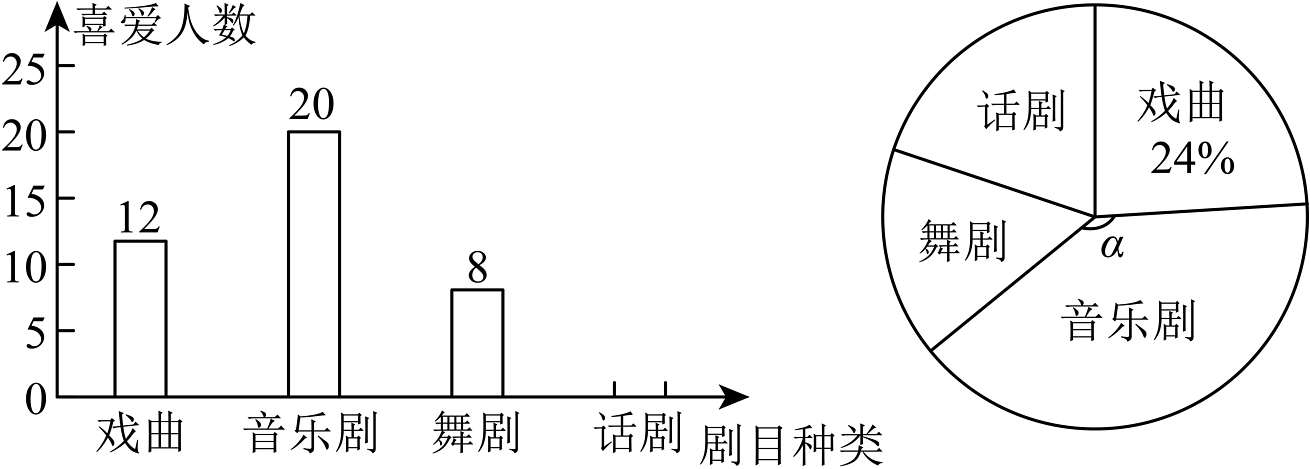 (1)、班级总人数为_______________人,__________________°;(2)、补全条形统计图;(3)、若小坪和小山所在的年级有800人,估计该年级喜欢舞剧的人数是多少?(4)、坪山大剧院周五,周六和周日将推出同一场音乐剧,假设小坪和小山分别打算去看这场音乐剧,且每一天去看音乐剧的可能性相同,那么在事先没有约好的情况下,小坪和小山选择同一日期看音乐剧的概率是多少?(请用画树状图或列表等方法说明理由).
(1)、班级总人数为_______________人,__________________°;(2)、补全条形统计图;(3)、若小坪和小山所在的年级有800人,估计该年级喜欢舞剧的人数是多少?(4)、坪山大剧院周五,周六和周日将推出同一场音乐剧,假设小坪和小山分别打算去看这场音乐剧,且每一天去看音乐剧的可能性相同,那么在事先没有约好的情况下,小坪和小山选择同一日期看音乐剧的概率是多少?(请用画树状图或列表等方法说明理由). -
6、先化简,再求值: , 再从 , 0,1,2中,选个合适的值作为代入求值.
-
7、(1)计算:;
(2)在解分式方程时,小亮的解法如下:
第一步:方程两边都乘 , 得 .
第二步:解这个方程,得 .
第三步:经检验,为原方程的解.
①在上述解方程过程中,从第______________步开始错误;
②错误的原因是____________________.
-
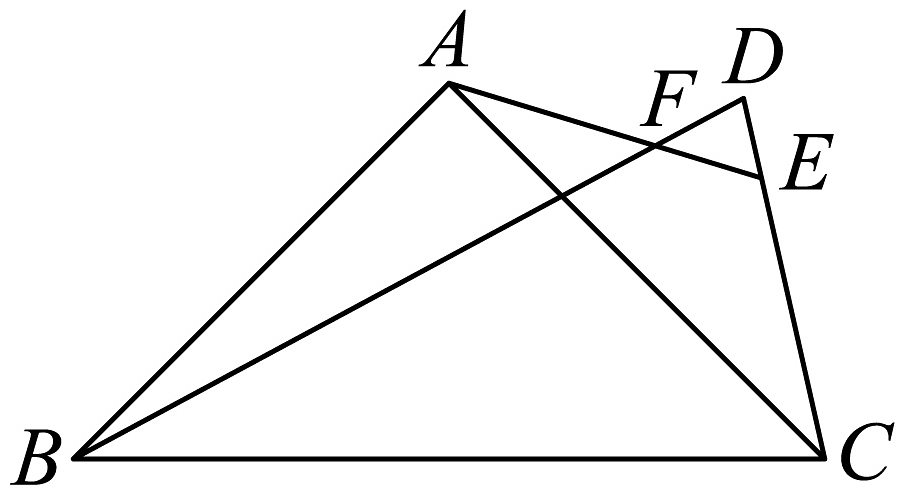
8、如图,在中, , , , 点在线段上且满足 , 与交于点 , 若 , 则 .
-
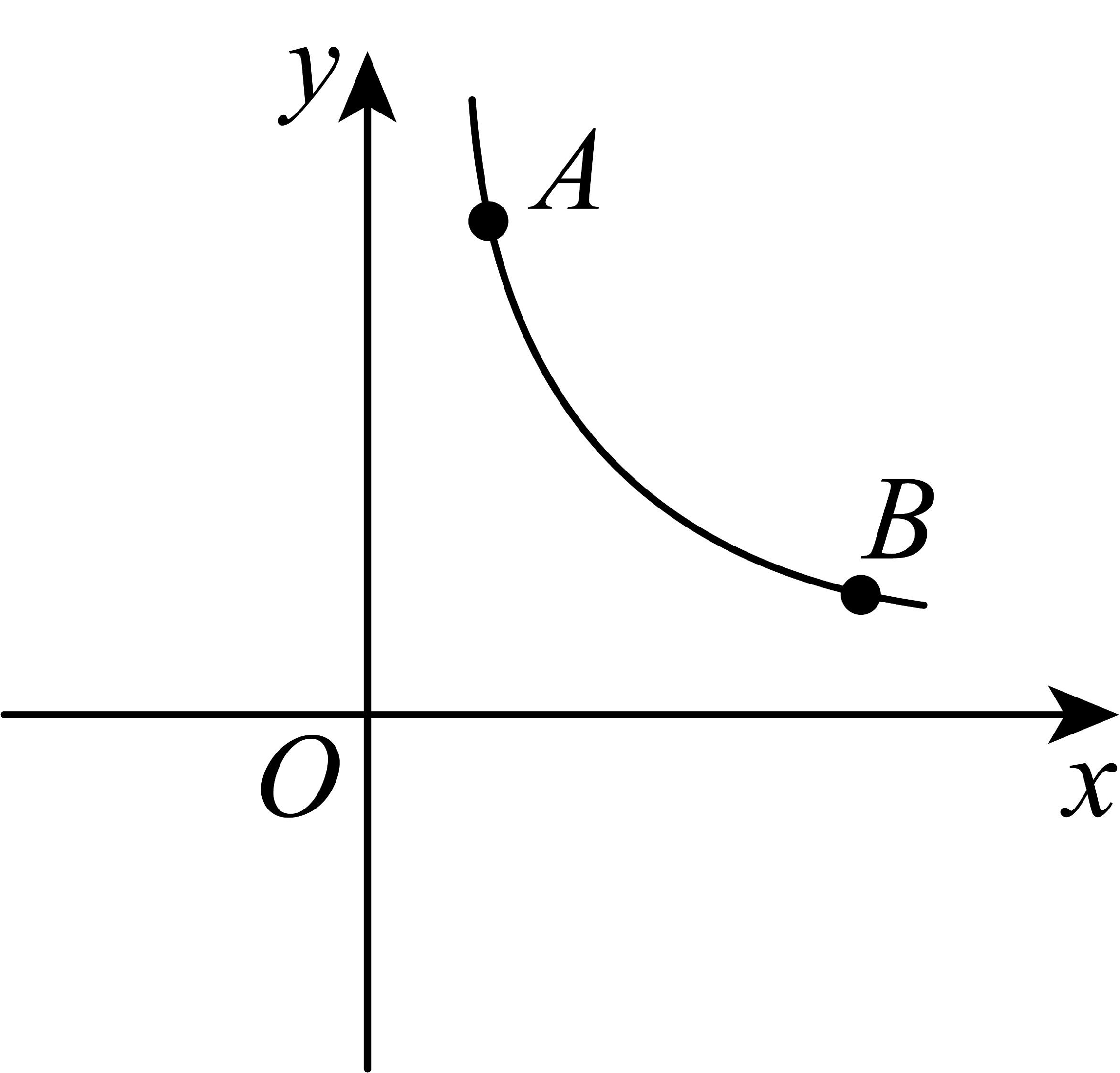
9、如图,在反比例函数上有两点和 , 若在第二象限存在一点 , 使得四边形为平行四边形,且平行四边形的面积为8,则点的坐标为 .
-
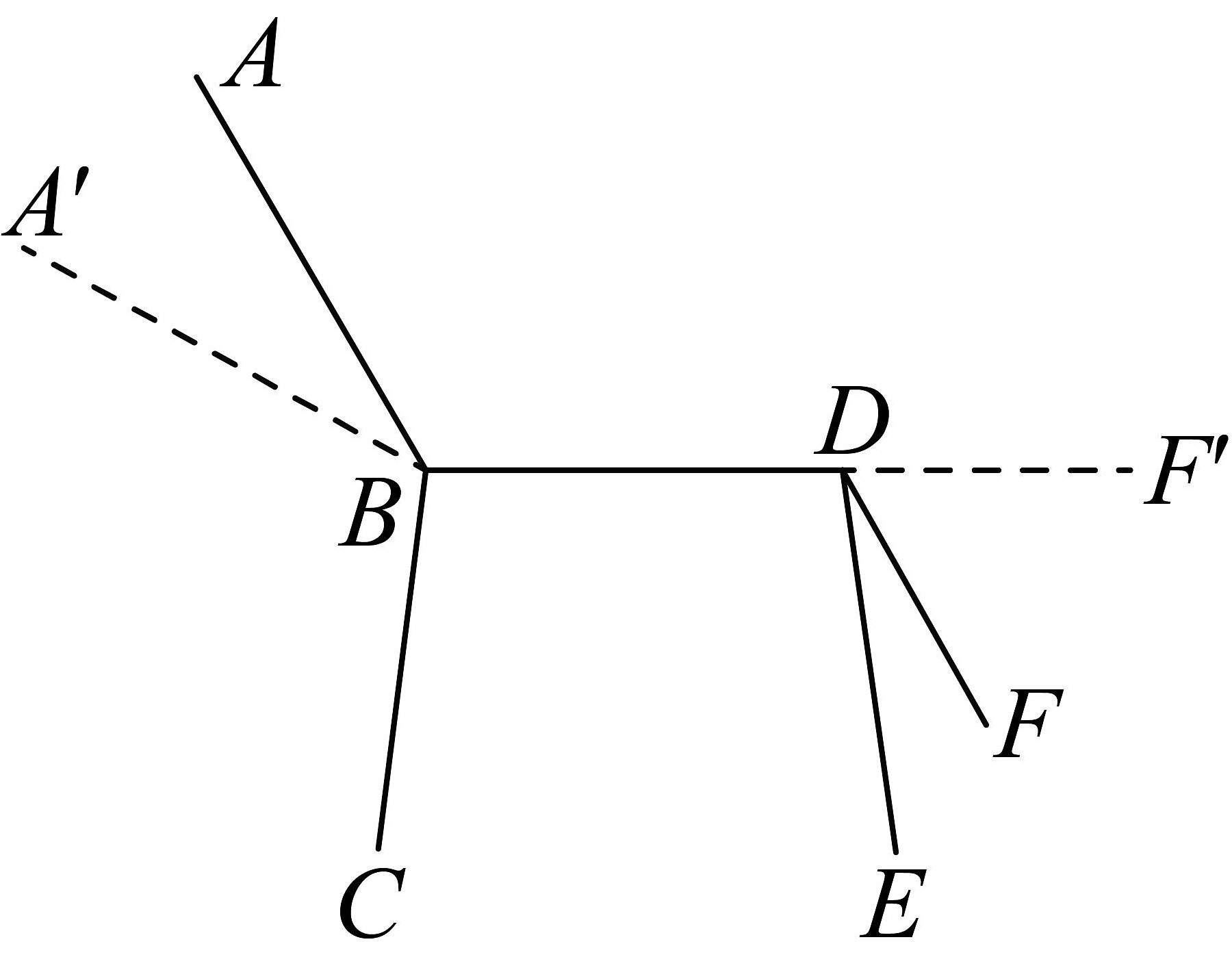
10、为了方便学生在校午休,某学校购入了一批可调节椅背且配备可折叠脚踏板的桌椅.若午休时椅背与椅座间的倾斜角达到 , 脚踏板拉起后与椅座在一条直线上,测量得到 , , , 则使用该椅子午休时方向的占地长度为 .
-
11、如图是李明在学校数学推理社团课的部分笔记,请根据笔记推理过程计算:( )
求的值
解:令 ,
则
故 ,
因此
A、 B、 C、 D、 -
12、随着科技的进步和人工智能技术的成熟,仿生机器狗有望成为人们生活中的重要伙伴.如图所示,仿生机器狗平稳站立时, , , , 此时的度数为( )
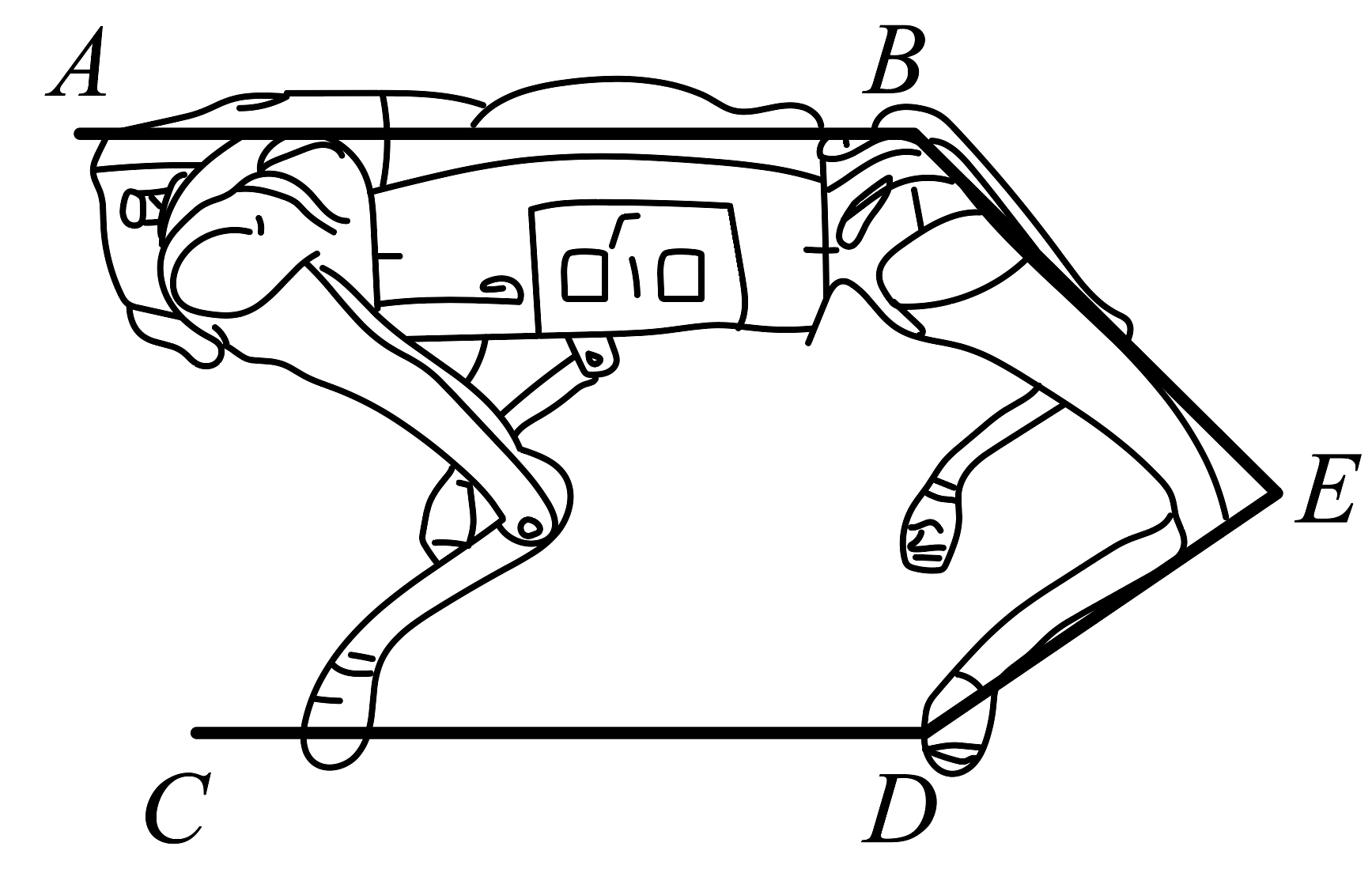 A、 B、 C、 D、
A、 B、 C、 D、 -
13、下列运算中结果正确的是( )A、 B、 C、 D、
-
14、深圳地铁14号线及16号线开通后,极大方便了坪山人民的日常出行.下列地铁图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
15、如图,在中, , 点D为边上一点,且 . 动点P从点A出发,沿以每秒1个单位长度的速度向终点B运动,且点P不与点A、B、D重合,过点P作交折线于点Q,作点P关于点D的对称点E,连接 . 设与重叠部分的面积为S,点P的运动时间为t(秒).
 (1)、当点Q与点C重合时, __________;(2)、用含t的代数式表示的长;(3)、当点E落在边上时,求S与t之间的函数关系式.
(1)、当点Q与点C重合时, __________;(2)、用含t的代数式表示的长;(3)、当点E落在边上时,求S与t之间的函数关系式. -
16、【模型学习】
构造“平行8字型”全等三角形模型是证明线段相等的一种方法.例如:如图①,D是的边上一点,E是的中点,过点C作 , 交的延长线于点F,可得到 .
【初步运用】
(1)如图②,在正方形中,点E是上一点,点F是的延长线上一点,且满足 , 连接交于点G,过点E作交于点M,则和的数量关系为__________;
【深入探究】
(2)如图②,在(1)的条件下,连接并延长,交于点H,若 , , 求正方形的边长;
【拓展迁移】
(3)如图③,在矩形中, , 点E在上,点F在的延长线上,且满足 , 连接交于点G.判断与之间的数量关系.

-
17、某快递物流总站送货,快递车出发小时后,因发现遗漏重要快递便驾小车沿相同路线追赶.已知快递车行驶的速度是千米/小时,小车行驶的速度是千米/小时.
 (1)、求小车出发后多少小时追上快递车?(2)、如图,图中 , 分别表示小车、快递车离开物流总站的路程(千米)与小车行驶的时间(小时)的函数关系的图象.试求所在直线的解析式;(3)、假设小车需要在1小时内追上快递车,因此出发追赶时通知快递车减速匀速行驶,求快递车至少减速至多少?
(1)、求小车出发后多少小时追上快递车?(2)、如图,图中 , 分别表示小车、快递车离开物流总站的路程(千米)与小车行驶的时间(小时)的函数关系的图象.试求所在直线的解析式;(3)、假设小车需要在1小时内追上快递车,因此出发追赶时通知快递车减速匀速行驶,求快递车至少减速至多少? -
18、【调查背景】
人工智能作为当下科技领域的热门议题,展现出广泛的应用场景与巨大的发展潜力.某学校为全面了解该校学生对人工智能的关注和认知程度,对全校学生开展了问卷调查.
【数据收集与整理】
测试得分采用得分制,得分越高,表明学生对人工智能的关注与了解程度就越高.现从该校学生中随机抽取80名学生的测试得分进行整理和分析(得分用x表示,且x为整数),共分为4组:A组 , 组 , 组 , 组 , 并绘制了如下不完整的统计图表.
被抽取学生的测试得分频数分布表
组别
频数
百分比
A
30
24
D
10

【数据分析与应用】
(1)、___________,__________;扇形统计图中C组对应的圆心角度数为__________;(2)、所抽取学生的测试得分的中位数在__________组;(3)、若得分不少于4分记为“合格”.已知该校共有5000名学生,估计该校对人工智能的了解程度“合格”的人数. -
19、“垃圾人桶,保护环境,从我做起”.图①是一种摇盖垃圾桶的实物图,图②是其侧面示意图,其盖子可整体绕点A所在的轴旋转.现测得 , , , , . 求点A到的距离(结果精确到 , 参考数据: , , ).

-
20、如图,一次函数的图象与反比例函数的图象相交于点 ,
 (1)、求和的值.(2)、横坐标为的点是反比例函数图象上的一点.现将点向下平移.当点落在一次函数图象上时,求向下平移的距离.
(1)、求和的值.(2)、横坐标为的点是反比例函数图象上的一点.现将点向下平移.当点落在一次函数图象上时,求向下平移的距离.