-
1、求|x-1|+|x-2|+|x-3|+…+|x-617|的最小值.
-
2、声波测距
在一条直道上同向行驶着两辆车，甲车在后，速度为90km/h，乙车在前，速度为72km/h，两车上都有声音的发播和接收装置，声音在空气中的传播速度为 340m/s.乙车在接收到甲车的鸣笛时会立即回鸣，甲车从发播到接收，经历的时间为7.2s.求甲车收到乙车的笛声时两车的距离(精确到0.01km). -
3、 A，B，C三辆车在同一条直路上同向行驶，某一时刻，A在前，C在后，B在A，C正中间.10分钟后，C追上B；又过了5分钟，C追上 A.问再过多少分钟，B追上?
-
4、如图，甲、乙两人分别在A，B两点同时相向而行，于E 点相遇后，甲继续向 B 行走，乙则休息了 14 分钟，再继续向A 行走.甲和乙到达B 和A 后立即折返，仍在E 点相遇.已知甲每分钟行走60米，乙每分钟行走80米，则A 和B 两点相距多少米?
-
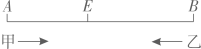
5、达妮卡开着她的新车走了整数小时，汽车平均时速为55千米，开始时里程表显示数字为 其中，abc(a≥1，a+b+c≤7).为一个三位数，停车时里程表显示数字为(cba，求 的值.
-
6、你追我赶
一直线上有A，B两个动点，动点 A 每前进1秒(速度为5米/秒)便停止3秒，并如此反复向前运动；当动点A 从点M 出发10 秒后，点B 从点 M 以3 米/秒的速度与点 A 同向前进.那么，当点 B 出发秒后便可追及点A.
-
7、甲、乙、丙三人一起进行百米赛跑(假定三人均为匀速直线运动)，如果当甲到达终点时，乙距终点还有5米，丙距终点还有10 米，那么当乙到达终点时，丙距终点还有米.
-
8、汽车A从甲站出发开往乙站，同时汽车B，C从乙站出发与 A 相向而行开往甲站，途中 A 与 B 相遇后 15 分钟再与 C 相遇.已知A，B，C的速度分别是每小时90km，80km，70km，那么甲、乙两站的距离是km.
-
9、甲、乙分别自A，B两地同时相向步行，2小时后中途相遇.相遇后，甲、乙步行速度都提高了1千米/时，当甲到达 B地后立刻按原路向A地返行，当乙到达 A 地后也立刻按原路向 B 地返行.甲、乙两人在第一次相遇后3小时36 分又再次相遇，则A，B两地的距离是千米.
-
10、甲、乙两运动员在长为100m的直道AB(A，B 为直道两端点)上进行匀速往返跑训练，两人同时从A 点起跑，到达 B 点后，立即转身跑向A 点，到达 A 点后，又立即转身跑向 B 点……若甲跑步的速度为5m/s，乙跑步的速度为 4m/s，则起跑后 100s内，两人相遇的次数为.
-
11、一轮船从甲地到乙地顺流行驶需4小时，从乙地到甲地逆流行驶需6小时，有一木筏由甲地漂流至乙地，需小时.
-
12、老师带着两名学生到离学校33千米远的博物馆参观，老师乘一辆摩托车，速度为25 千米/时，这辆摩托车后座可带乘一名学生，带人速度为20千米/时，学生步行的速度为5千米/时，请你设计一种方案，使师生三人同时出发后到达博物馆的时间都不超过3个小时.
-
13、甲、乙二人分别从 A，B两地同时出发，在距离 B地6千米处相遇，相遇后两人又继续按原方向、原速度前进，当他们分别到达 B地，A地后，又在距A地4千米处相遇.求A，B两地相距多少千米?
-
14、有甲、乙两辆小汽车模型，在一个环形轨道上匀速行驶，甲的速度大于乙.如果它们从同一点同时出发沿相反方向行驶，那么每隔 分钟相遇一次.现在，它们从同一点同时出发，沿相同方向行驶，当甲第一次追上乙时，乙已经行驶了4圈，此时它们行驶了多少分钟?
-
15、甲、乙两动点分别从正方形 ABCD 的顶点A，C同时沿正方形的边开始移动.甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的4倍，则它们第2000 次相遇在边( ).
A、AB上 B、BC上 C、CD上 D、DA 上 -
16、(1)、在公路上，汽车 A，B，C分别以 80km/h，70km/h，50km/h的速度匀速行驶，A从甲站开往乙站，同时，B，C从乙站开往甲站. A在与B相遇2小时后又与C相遇，则甲、乙两站相距km.(2)、小王沿街匀速行走，他发现每隔6min 从背后驶过一辆18路公交车；每隔3min迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同，而且18路总站每隔固定时间发一辆车，那么，发车的间隔时间为min.
-
17、把数字1，2，3，…，9 分别填入图中的 9 个圈内，要求三角形 ABC 和三角形 DEF 的每条边上三个圈内数字之和都等于18.
(1)、给出一种符合要求的填法.(2)、共有多少种不同填法?证明你的结论. -
18、你能在图中的3×3的方格表中的每个格子里都填上一个自然数，使得每行、每列及每条对角线上的三数之和都等于2017吗?若能，请填出一例；若不能，请说明理由.
-
19、(1)、如图①，在3阶幻方中，只填入了3个数，请将剩余的6个数直接填入到表中(用含a的代数式分别表示这6个数，写出一种情况即可).
(2)、如图②，在3阶幻方中，只填入了2个数，请你求出右上角“?”所表示的数值.
-
20、幻方第一人
幻方，相传最早见于我国的“洛书”，如图①，洛书中3行、3列以及2条对角线上的点数之和都等于15，是一种“3阶幻方”(如图②).我国南宋数学家杨辉是对幻方从数学角度进行系统研究的第一人，他在《续古摘奇算法》一书中给出从3 阶到 10 阶的幻方，并对一些低阶幻方介绍了构造方法，其中运用了对称思想.例如，用1，2，3，…，16构造4阶幻方的方法是：先将1，2，3，…，16依次排成图③，然后以外四角对换，即1 与16 对换，4与13 对换，再以内四角对换……请你在图④中填写用这种“对换”方法得出的4阶幻方.
