-
1、“绿水青山就是金山银山”,为了绿色发展,某林场计划购买甲、乙两种树苗,已知购买一株甲种树苗的进价比一株乙种树苗的进价少3元,用3000元购进甲种树苗的数量是用3200元购进乙种树苗的数量的1.5倍.(1)、求每株甲种树苗,每株乙种树苗的进价分别为多少元?(2)、相关资料表明:甲、乙两种树苗的成活率分别为和 . 为保证绿化效果,林场决定再购买甲、乙两种树苗共100株.若要使这批树苗的成活率不低于 , 且购买树苗的总费用最低,应如何选购树苗?
-
2、一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高和脚长之间近似存在一个函数关系,部分数据如下表:
脚长
…
…
身高
…
…
 (1)、在图1中描出表中数据对应的点;(2)、根据表中数据,从和中选择一个函数模型,使它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出的取值范围);(3)、如图2,某场所发现了一个人的脚印,脚长约为 , 请根据(2)中求出的函数解析式,估计这个人的身高.
(1)、在图1中描出表中数据对应的点;(2)、根据表中数据,从和中选择一个函数模型,使它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出的取值范围);(3)、如图2,某场所发现了一个人的脚印,脚长约为 , 请根据(2)中求出的函数解析式,估计这个人的身高. -
3、如图,在中, , . 完成以下两个小题的解答:
 (1)、用尺规作的中点 , 并以为半径作(不写作法,保留作图痕迹),求证:与边相切;(2)、若恰好交于边的中点,求的半径长.
(1)、用尺规作的中点 , 并以为半径作(不写作法,保留作图痕迹),求证:与边相切;(2)、若恰好交于边的中点,求的半径长. -
4、如图,在平面直角坐标系中,反比例函数的图象和都在第一象限内, , 轴,且 , 点的坐标为 . 将向下平移个单位长度, , 两点的对应点恰好同时落在反比例函数图象上,则 .

-
5、若+有意义,则(-n)2的平方根是( )A、 B、 C、± D、±
-
6、如图所示,已知 , 点在线段上(不与点、点重合), , . 则的值为( )
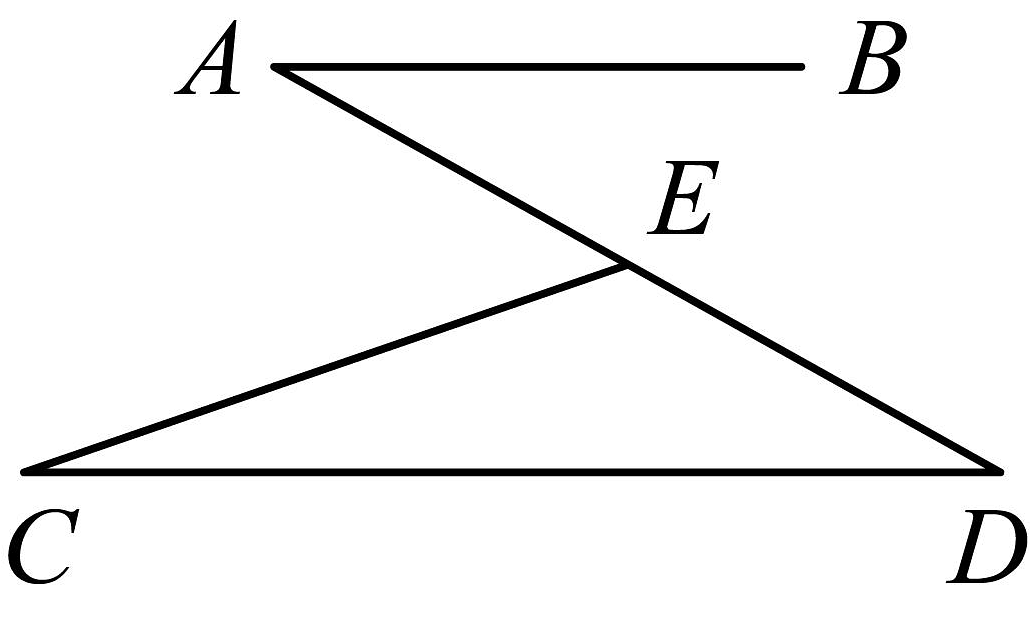 A、 B、 C、 D、
A、 B、 C、 D、 -
7、计算:( )A、 B、14 C、 D、
-
8、在综合与实践活动中,“特殊到一般”是一种常用的方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论.
如图1,在正方形纸片中,点是边上一动点(不与端点重合).折叠正方形纸片,使点与点重合,折痕分别交边、于点M、N,的对应边为 , 与交于点 . 探究的周长与边的等量关系,并证明你的结论.
【特殊化感知】
(1)先从简单的、特殊的情况开始研究:若 , 点恰好是边的中点,则______;
【一般化探究】
(2)对正方形的边长一般化处理,并改变点的位置:如图2,若 , 求的周长(用含的代数式表示);
【拓展性延伸】
(3)通过(1)(2)的解决,可猜想出的周长与边的等量关系.但由于边长的一般化及点位置的不确定,会导致、、的长度也不确定,从而使代数计算显得非常繁琐,那能否从几何角度证明若干个不确定的长度之和是确定的呢?请猜想的周长与边的等量关系,并证明你的结论.



-
9、【模型构建】
如图,将含有的三角板的直角顶点放在直线上,过两个锐角顶点分别向直线作垂线这样就得到了两个全等的直角三角形,由于三个直角的顶点都在同一条直线上,因此我们将其称为“一线三直角”,这模型在数学解题中被广泛使用.
【模型应用】
(1)如图1,在平面直角坐标系中,直线与轴,轴分别交于 , 两点,
①则点坐标为______;点坐标为______;
② , 是正比例函数图象上的两个动点,连接 , , 若 , , 则的最小值是______;
(2)如图2,一次函数的图象与轴,轴分别交于 , 两点.将直线绕点逆时针旋转得到直线 , 求直线对应的函数表达式;
【模型拓展】
(3)如图3,直线的图象与轴,轴分别交于、两点,直线与轴交于点 . 点、分别是直线和直线上的动点,点的坐标为 , 当是以为斜边的等腰直角三角形时,直接写出点的坐标.

-
10、如图1,和是半径为2的的两条直径,点P是延长线上的一点.连接交于点E(点E在线段上,且不与点P、点C重合).
 (1)、当时,求证:;(2)、连接 , 交半径于点M,已知 .
(1)、当时,求证:;(2)、连接 , 交半径于点M,已知 .①连接 , 如图2,当点M是的重心时,求的余弦值;
②连接、 , 当为等腰三角形时,求线段的长.
-
11、某中学开展物理跨学科综合实践活动,作有关大气压的测量实验,需要准备红色和黄色两种气球,学校计划前往某超市购买.通过调查,将获取的相关数据整理如下表:
购买数量(单位:包)
总费用(单位:元)
红色气球
黄色气球
3
4
85
2
3
60
(1)、红色气球、黄色气球每包各是多少元?(2)、该中学决定购买红色和黄色两种气球共100包,且总费用不超过1300元,那么该中学至少可以购买多少包黄色气球? -
12、某校提倡数学学习与生活紧密结合,数学问题要源于生活,用于生活.为此学校开展了以“生活中的数学”为主题的知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:
A. , B. , C. , D.),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99 80 99 86 99 96 90 100 89 82
八年级10名学生的竞赛成绩是:
 94 90 94
94 90 94  (部分数据被污染)
(部分数据被污染)七、八年级抽取的学生竞赛成绩统计表
年级
平均数/分
中位数/分
众数/分
方差
七年级
92
93
a
52
八年级
92
b
100
50.4
八年级抽取的学生竞赛成绩条形统计图

根据以上信息,解答下列问题:
(1)、直接写出 , , 并补全条形统计图.(2)、该校七、八年级参加此次竞赛活动的人数分别为600人和700人,估计在本次竞赛活动中七、八年级成绩优秀()的学生共有多少人.(3)、分析上述信息,你认为该校七、八年级中哪个年级学生掌握“生活中的数学”知识较好?请说明理由(一条即可). -
13、(1)计算:;
(2)化简: .
-
14、如图,把置于平面直角坐标系中,点的坐标为 , 点的坐标为 , 点是内切圆的圆心.将沿轴的正方向作无滑动滚动,使它的三边依次与轴重合,第一次滚动后圆心为 , 第二次滚动后圆心为 , 依此规律,第2025次滚动后,内切圆的圆心的坐标是 .

-
15、已知是方程组的解,则 .
-
16、若式子有意义,则的取值范围是 .
-
17、如图,在菱形中, , , 点在边上,且 , 是边上一动点,将沿直线折叠,点落在点处,当点在四边形内部(含边界)时,的长度的最小值是( )
 A、2 B、 C、4 D、
A、2 B、 C、4 D、 -
18、关于的二次函数(为常数,)的图象可能是( )A、
 B、
B、 C、
C、 D、
D、
-
19、《低空经济产业发展白皮书》指出,我国低空经济产业具有巨大的发展潜力,未来将对国民经济作出重要贡献年我国低空经济规模为万亿元,预计年我国低空经济规模将达到万亿元.如果设这两年低空经济规模年平均增长率为 , 那么根据题意可列方程( )A、 B、 C、 D、
-
20、下列计算正确的是( )A、 B、 C、 D、