相关试卷

1、已知抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = 1$ ，与 $y$ 轴的交点位于 $x$ 轴下方，且 $x = - 1$ 时， $y > 0$ ，下列结论正确的是（）

A、 $2 a = b$ B、 $b^{2} - 4 a c < 0$ C、 $a - 2 b + 4 c < 0$ D、 $8 a + c > 0$

查看解析
2、《九章算术》是中国古代一部重要的数学著作，在“方程”章中记载了求不定方程（组）解的问题．例如方程 $x + 2 y = 3$ 恰有一个正整数解 $x = 1, y = 1$ ．类似地，方程 $2 x + 3 y = 21$ 的正整数解的个数是（）

A、1 B、2 C、3 D、4

查看解析
3、如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $B D$ 为 $⊙ O$ 的直径．若 $A B = A C, ∠ A C B = 70 °$ ，则 $∠ C B D =$ （）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看解析
4、矩形具有而菱形不具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角相等

查看解析
5、某校七年级甲、乙、丙、丁四名同学参加1分钟跳绳测试，每人10次跳绳成绩的平均数（单位：个）及方差（单位：个²）如下表所示：
甲
乙
丙
丁
平均数
205
217
208
217
方差
4.6
4.6
6.9
9.6
根据表中数据，要从中选择一名成绩好且发挥稳定的同学参加比赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看解析
6、下列运算正确的是（）

A、 $4 a - 3 a = 1$ B、 ${(2 a)}^{- 1} = \frac{2}{a}$ C、 ${(3 a^{3})}^{2} = 9 a^{6}$ D、 ${(a - b)}^{2} = a^{2} - b^{2}$

查看解析
7、下列人工智能助手图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看解析
8、如图，直线 $a ∥ b$ ，若 $∠ 1 = 132 °$ ，则 $∠ 2 =$ （）

A、 $42 °$ B、 $48 °$ C、 $52 °$ D、 $58 °$

查看解析
9、据我国文化和旅游部数据中心测算，2025年“五一”期间，国内游客出游 $314000000$ 人次，将数据 $314000000$ 用科学记数法表示为（）

A、 $31.4 \times 10^{7}$ B、 $3.14 \times 10^{7}$ C、 $3.14 \times 10^{8}$ D、 $3.14 \times 10^{9}$

查看解析
10、下列各组数中，互为相反数的是（）

A、 $7$ 和 $- 7$ B、 $3$ 和 $- 2$ C、2和 $\frac{1}{2}$ D、 $- 0.1$ 和 $10$

查看解析
11、如图，直线 $y = - \frac{12}{5} x + 12$ 与x轴交于A，与y轴交于B．直线 $B C$ 与 $A B$ 关于y轴对称．将 $B C$ 向左平移经过点 $D (- 13, 12)$ ，与x轴交于E．F在 $D B$ 的延长线上，G在第四象限直线 $A B$ 上， $E F$ 与 $D G$ 交于P．

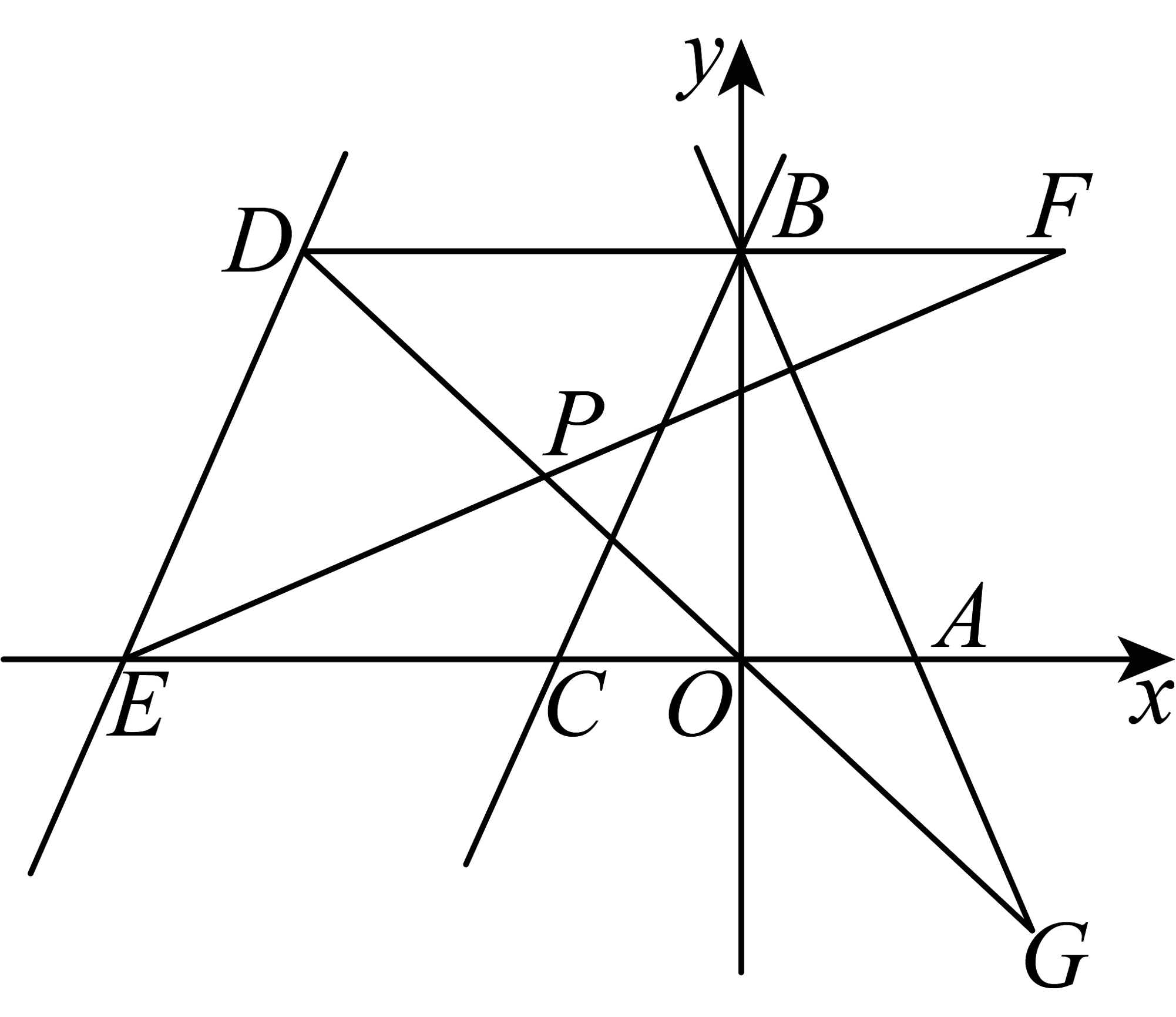(1)、求直线 $D E$ 的解析式．

(2)、判断四边形 $B D E C$ 的形状，并证明你的结论．

(3)、当动点F，G满足 $A G = B F$ 时，求证： $E F = D G$ ．

查看解析
12、如图，平行四边形ABCD中，AE⊥CD于E，BF平分∠ABC与AD交于F．AE与BF交于G．
（1）延长DC到H，使CH＝DE，连接BH．求证：四边形ABHE是矩形．
（2）在（1）所画图形中，在CH的延长线上取HK＝AG，当AE＝AF时，求证：CK＝AD．

查看解析
13、如图，过点 $A (- 2, 0)$ 的直线 $l_{1} : y = k x + b$ 与直线 $l_{2} : y = - x + 1$ 交于 $P (- 1, a)$ ．

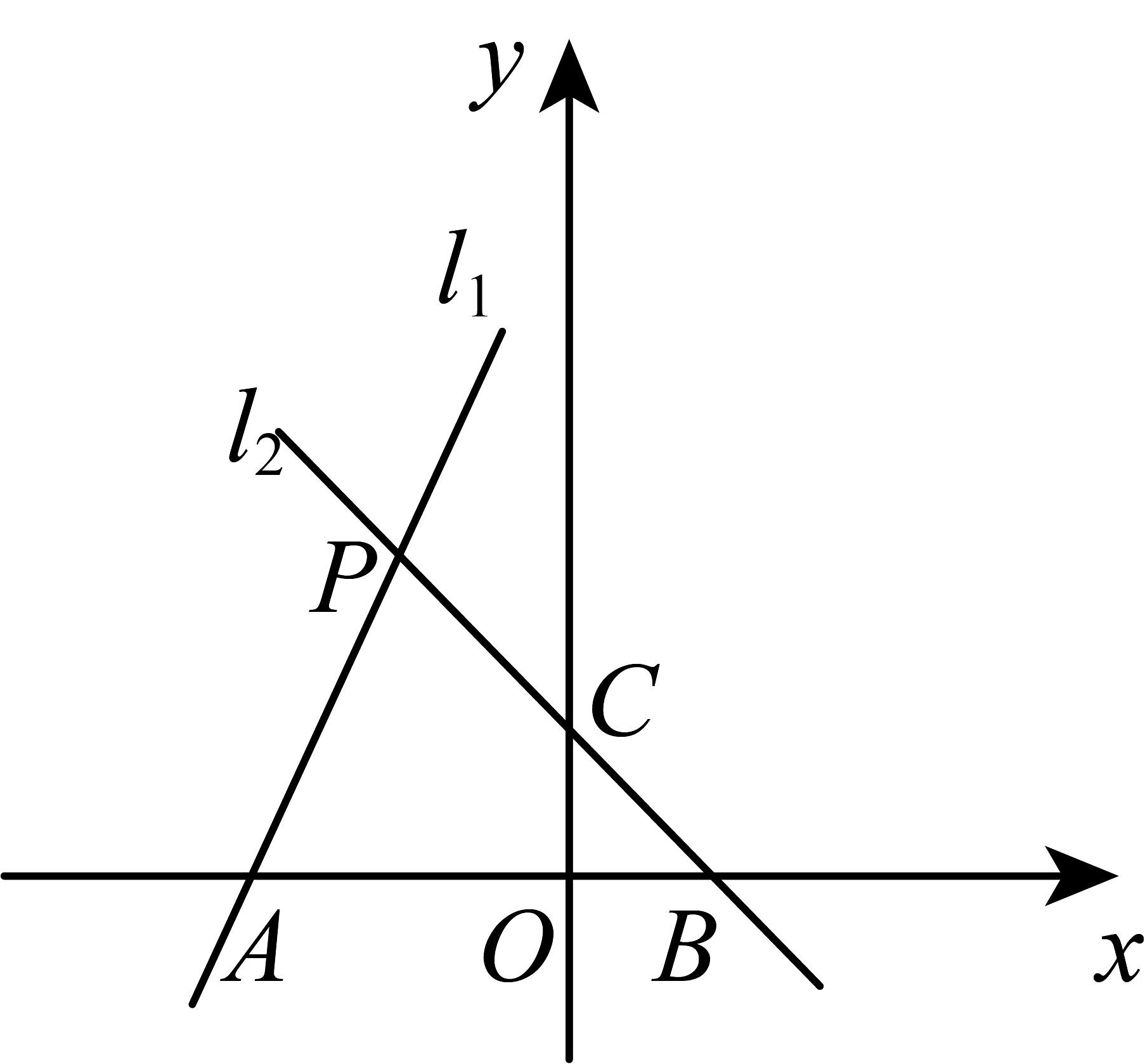(1)、求直线 $l_{1}$ 对应的表达式；

(2)、求四边形 $P A O C$ 的面积．

查看解析
14、如图，四边形ABCD中，E为边BC的中点，BD与AE交于O，BO＝DO，AO＝2EO．AC与BD交于F．
（1）求证：F是AC的中点．
（2）求S_△_ACD：S_△_ABD的值．

查看解析
15、为庆祝中华人民共和国成立73周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买2个甲种文具、1个乙种文具共需花费35元；购买1个甲种文具、3个乙种文具共需花费30元．

(1)、求购买一个甲种文具、一个乙种文具各需多少元？

(2)、若学校计划购买这两种文具共120个，投入资金不少于955元又不多于1000元，求有多少种购买方案？哪种购买方案需要的资金最少？

查看解析
16、某校要在甲、乙两名同学中选择一人参加市级的演讲比赛，对他们演讲材料、语言表达、形体语言三方面进行测评，根据综合成绩择优去参加比赛．他们的各项成绩．如表所示：
候选人
演讲材料
语言表达
形体语言
甲
93分
87分
83分
乙
88分
96分
80分

(1)、如果把各项成绩的平均数作为综合成绩，应该让谁参加比赛？

(2)、如果把演讲材料、语言表达、形体语言三方面成绩分别按照 $\frac{1}{2}$ ， $\frac{3}{10}$ ， $\frac{1}{5}$ 的权重计入综合成绩，应该让谁参加比赛？

查看解析
17、先计算 $3 \sqrt{48} - 5 \sqrt{12} + 6 \sqrt{\frac{1}{3}}$ 的结果，再确定其结果在哪两个整数之间．

查看解析
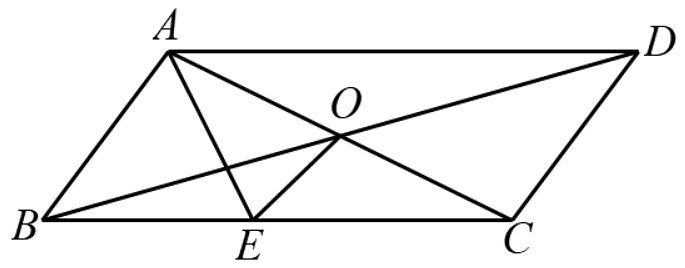
18、如图，▱ABCD中，AC，BD交于O，AE平分∠BAD，EC＝CD＝1，∠ECD＝2∠CDA．下列结论：①AC平分∠EAD；②OE＝ $\frac{1}{4}$ AD；③BD＝ $\sqrt{7}$ ；④S▱ABCD＝ $\sqrt{3}$ ．正确的有个．

查看解析
19、如图，在直角坐标系中，矩形OABC的两邻边在坐标轴上，顶点B（6，4），经过边BC上一点P（4，m）的直线将矩形面积平分，则这条直线的解析式为．

查看解析
20、如图，点P（﹣4，3）在一次函数y＝kx＋b（k≠0）的图象上，则关于x的不等式kx＋b＜3的解集是．

查看解析

上一页 898 899 900 901 902 下一页跳转

候选人	演讲材料	语言表达	形体语言
甲	93分	87分	83分
乙	88分	96分	80分

	甲	乙	丙	丁
平均数	205	217	208	217
方差	4.6	4.6	6.9	9.6