-
1、已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为: , 相应的△ABP的面积关于运动时间的函数图象如图2,若 , 则下列四个结论中正确的个数有( )
①图1中的BC长是8cm ②图2中的M点表示第4秒时y的值为24
③图1中的CD长是4cm ④图2中的N点表示第12秒时y的值为18
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
2、如图,将矩形ABCD沿AE折叠,使点B落在边CD上点F处,若AD=8cm,CE=3cm,则边AB的长为( )
 A、9cm B、10cm C、12cm D、13cm
A、9cm B、10cm C、12cm D、13cm -
3、如图,某学校抽查了10名八年级学生的数学期中成绩,则这10名学生的数学平均成绩为( )
 A、88 B、87 C、86 D、85
A、88 B、87 C、86 D、85 -
4、如图,正方形ABCD中,点O在△ACD内,∠OAC=∠ODA,则∠AOD=( )
 A、120° B、125° C、130° D、135°
A、120° B、125° C、130° D、135° -
5、如图,四边形ABCD中,∠B=∠D=90°,AB=3 , BC=4 , AD=CD,则AD•CD( )
 A、12 B、24 C、12 D、25
A、12 B、24 C、12 D、25 -
6、如图,在中, , 垂足为 , 为上的一点, , 分别交和的延长线于点 , , .
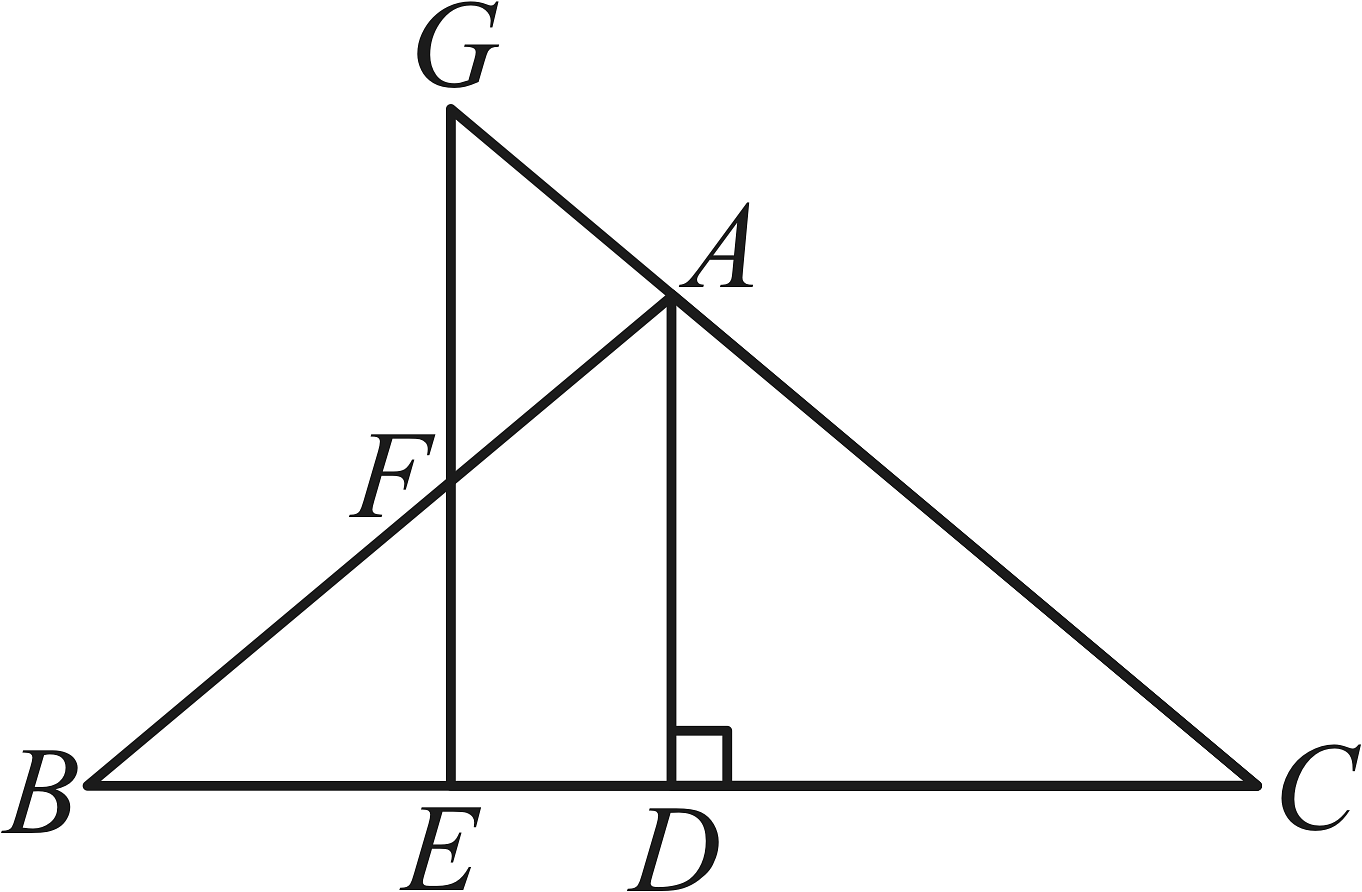 (1)、试说明;(2)、若 , 求和的大小.
(1)、试说明;(2)、若 , 求和的大小. -
7、如图点为的重心.已知的面积为2,则的面积为 .

-
8、为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文 . 例如,明文1,2,3,4对应密文5,7,10,8.当接收方收到密文14,9,24,28时,则解密得到的明文四个数字之和为 .
-
9、如图,M为矩形纸片的边的中点,将纸片沿折叠,使点A落在处,点D落在处.若 , 则的度数为 .

-
10、若是一个完全平方式,则 .
-
11、如图1,点是线段上的动点(点与不重合),分别以为边向线段的同一侧作正和正.

(1)请你判断与有怎样的数量关系?请说明理由;
(2)连接 , 相交于点 , 设 , 那么的大小是否会随点的移动而变化?请说明理由;
(3)如图2,若点固定,将绕点按顺时针方向旋转(旋转角小于),此时的大小是否发生变化?(只需直接写出你的猜想,不必证明)
-
12、如图是一种躺椅及其简化结构示意图,扶手与底座都平行于地面,靠背与支架平行,后支架过D点,交于G,与交于N,当与正好垂直,时,人躺着最舒服,求此时的度数.

-
13、先化简,再求值: , 其中 , .
-
14、计算:(1)、(2)、
-
15、不透明袋子中装有10个球,其中有8个绿球、2个红球,这些球除颜色外无其他差别,现再放入n个除颜色外无其他差别的红球,如从袋子中随机取出1个球,它是红球的概率为 , 那么n的值为 .
-
16、如图,用两根拉线固定竖直电线杆的示意图,其中拉线的长 , 若 , 则 .

-
17、如图,正方形的面积为9,是等边三角形,点在正方形内,在对角线上有一点 , 使的和最小,则这个最小值为( )
 A、3 B、6 C、9 D、4
A、3 B、6 C、9 D、4 -
18、已知变量x、y满足下面的关系如表所示,则x、y之间用关系式表示为( )
x
…
1
2
3
…
y
…
1
3
…
A、 B、 C、 D、 -
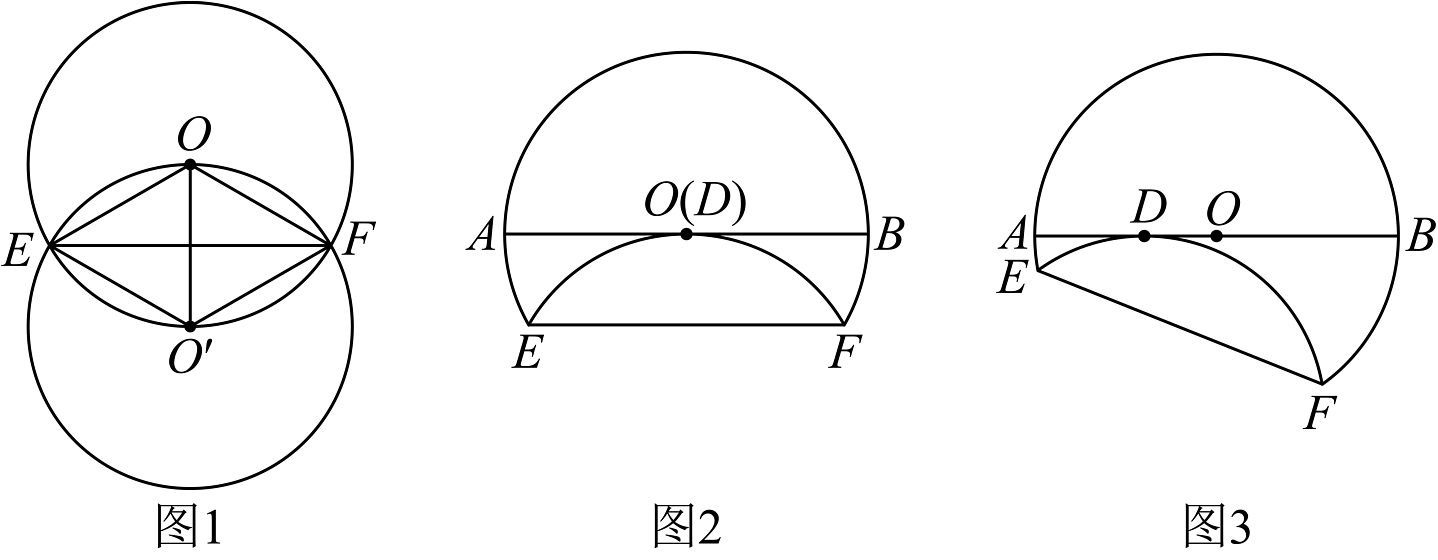
19、综合探究:(1)、如图1,等圆与相交与点与点 , 连接 , 证明四边形为菱形.(2)、如图2,已知的直径为10,以线段为折痕进行折叠,使得与直径相切于点 , 若折叠后与点重合,求此时的长度.(3)、如图3,在题(2)中,改变与直径相切的切点的位置.若折叠后切点与圆心的长度 , 求折痕的长度.
-
20、实践与研究:(1)、根据下面列表,在同一直角坐标系中画出函数和的图像.
…
1
2
3
…
…
4
2
…
…
0
2
3
4
…
…
4
2
…
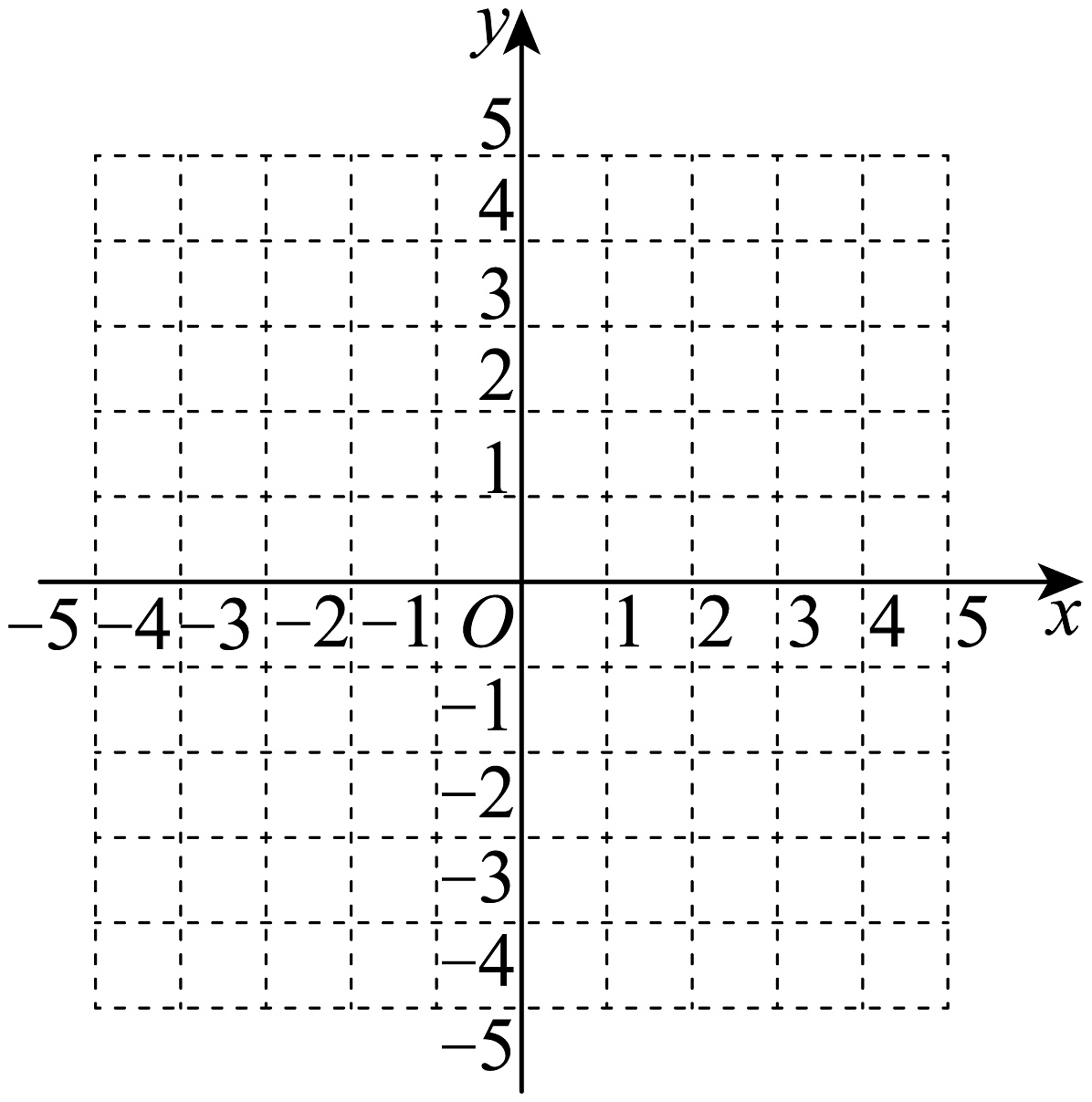 (2)、观察两个函数图象,的图像可以由的图像怎么变换得到?(3)、当动直线与在第一象限内只有一个交点时,交点坐标为 , 若与在轴右侧的图像无交点,试确定的取值范围.
(2)、观察两个函数图象,的图像可以由的图像怎么变换得到?(3)、当动直线与在第一象限内只有一个交点时,交点坐标为 , 若与在轴右侧的图像无交点,试确定的取值范围.