-
1、【问题情境】
如图1,这是一种电风扇的横截面示意图,点为电风扇横截面的圆心,为底座下部的圆的直径,若连接 , 则与分别交于两点,且 .

【问题探究】
(1)如图2,设是线段的中点,连接交于点 . 过点作 , 分别交 , 于点 , , 求证:是的切线.
【问题解决】
(2)如图2,连接 , 经测量可得 , , , 求电风扇的半径的长.
-
2、图1是一辆在平地上滑行的滑板车,图2是其示意图.已知车杆长 , 车杆与脚踏板所成的角 , 前后轮子的半径均为 , 求把手A离地面的高度(参考数据: , , ).

-
3、计算:
-
4、如图,圆锥的侧面展开图是一个圆心角为的扇形,若扇形的半径l是5,则该圆锥的表面积是 .

-
5、定义关于任意正整数的一种新运算: . 例如,规定 , 则 , . 若规定 , 则( )A、 B、 C、 D、
-
6、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则的正切值是( )
 A、2 B、 C、 D、
A、2 B、 C、 D、 -
7、一位同学把一副三角板在桌面上摆放成如图所示形状, , , , 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、下列运算正确的是( )A、 B、 C、 D、
-
9、纹样作为中国传统文化的重要组成部分,是古人智慧与艺术的结晶,反映出不同时期的风俗习惯,早已融入我们的生活.下面纹样的示意图中,是中心对称图形,但不是轴对称图形的是( )A、
 如意纹
B、
如意纹
B、 冰裂纹
C、
冰裂纹
C、 盘长纹
D、
盘长纹
D、 风车纹
风车纹
-
10、“十二年学习在南外,十二年成长在深圳湾”的南外集团教育历程和“葆有外语特色,做强数理实力”的南外教育内涵获得了全社会的广泛认可.为了不断提升学生对南外集团的归属感,集团举办了一次南外校史知识竞赛,并随机抽取部分学生,将竞赛成绩按以下五组进行整理(得分用x表示):A: , B: , C: , D: , E: , 并绘制出如图的统计图1和图2.
请根据相关信息,解答下列问题:
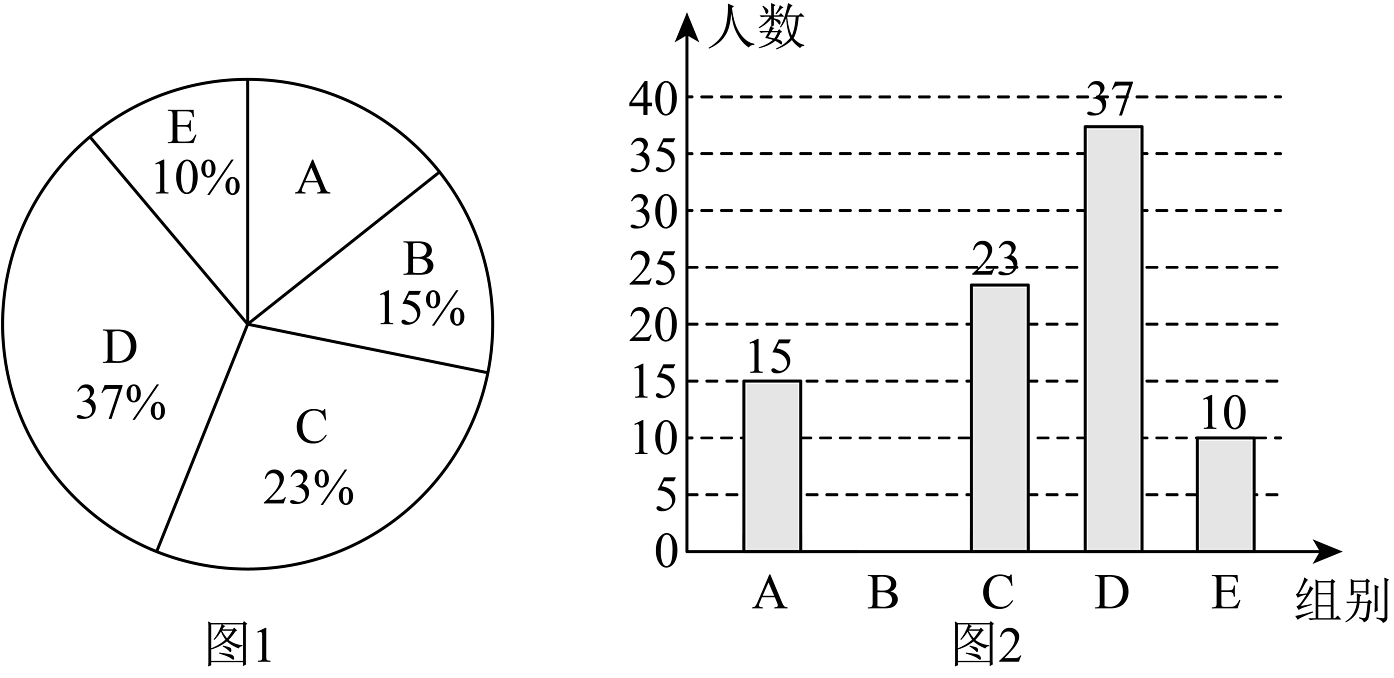 (1)、图1中A组所在扇形的圆心角度数为 ___________°,并将条形统计图补充完整.(2)、若“”这一组的数据为:90,96,92,95,93,96,96,95,97,100.则这组数据的众数是 ___________,中位数是 ___________.(3)、经过初赛,进入决赛的同学有1名女生(记为A)和2名男生(记为B,C),现从这三位同学中决出冠亚军,请用列表或画树状图法求冠亚军的两人恰好是一男一女的概率.
(1)、图1中A组所在扇形的圆心角度数为 ___________°,并将条形统计图补充完整.(2)、若“”这一组的数据为:90,96,92,95,93,96,96,95,97,100.则这组数据的众数是 ___________,中位数是 ___________.(3)、经过初赛,进入决赛的同学有1名女生(记为A)和2名男生(记为B,C),现从这三位同学中决出冠亚军,请用列表或画树状图法求冠亚军的两人恰好是一男一女的概率. -
11、如图所示,已知二次函数图象与直线相交于点 , 直线交轴于 , 点为抛物线上一点,将点绕着原点逆时针旋转得到对应点 , 连接 .
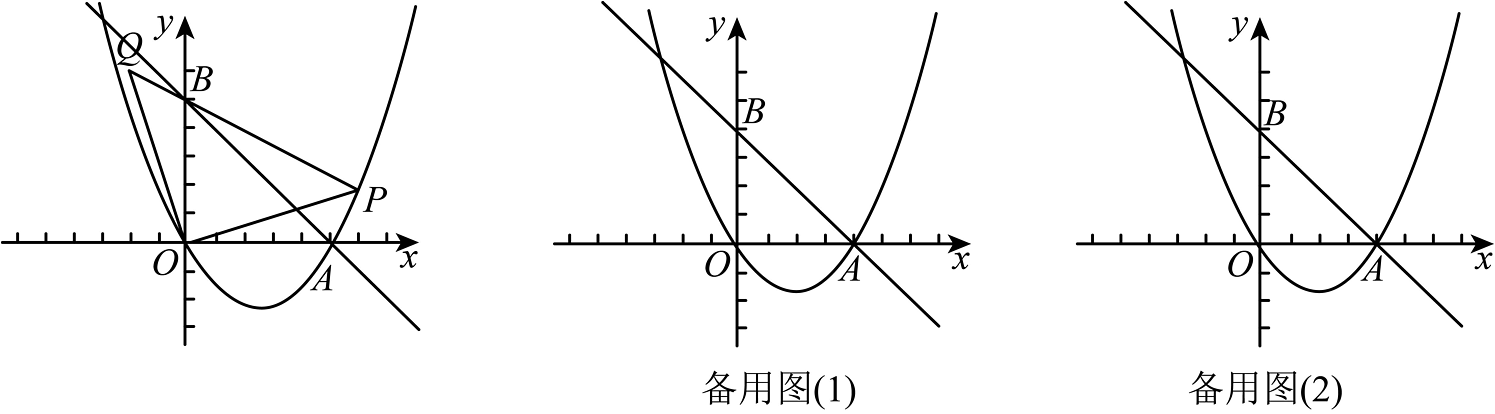 (1)、求抛物线和直线的函数解析式.(2)、当点坐标为时,求证:点 , , 三点在同一直线上.(3)、当有一顶点在直线上时,
(1)、求抛物线和直线的函数解析式.(2)、当点坐标为时,求证:点 , , 三点在同一直线上.(3)、当有一顶点在直线上时,①求长;
②在①的条件下,当点在第四象限时,在上取点 , 在上取点 , 使 , 连接 , , 求的最小值.
-
12、定义:在直角梯形中,若斜腰与梯形的一条底边相等,则此直角梯形被称为“斜腰等底直角梯形”.
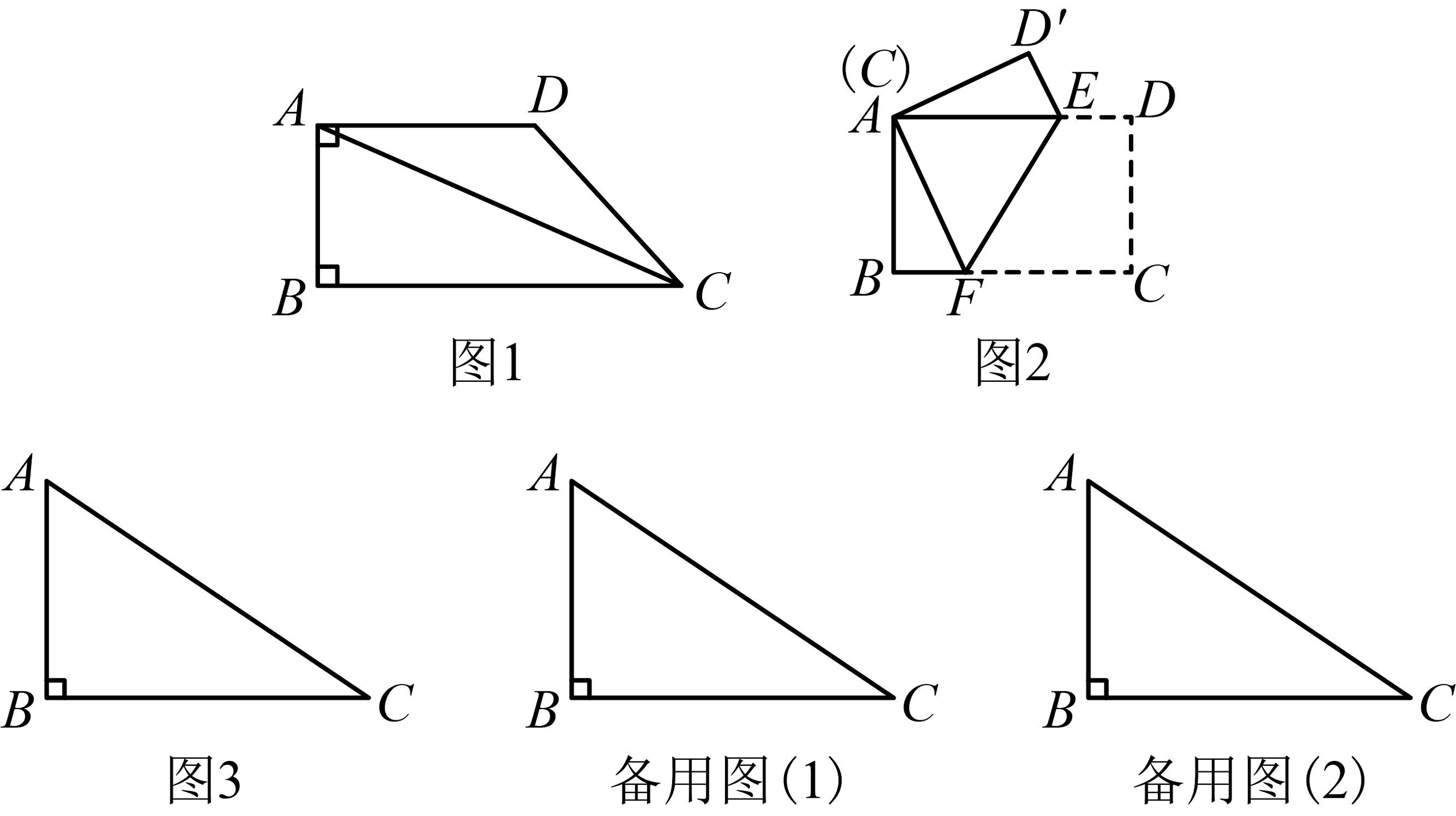 (1)、如图1所示,直角梯形为“斜腰等底直角梯形”, , , , 连接 , 求证:平分;(2)、如图2所示,在矩形中,折叠矩形,使点 , 重合,折痕为 , 点的对应点为 , 当时,求证:四边形为“斜腰等底直角梯形”;(3)、如图3所示,在中, , , , 若以 , 为边画四边形 , 当四边形是“斜腰等底直角梯形”时,直接写出的长.
(1)、如图1所示,直角梯形为“斜腰等底直角梯形”, , , , 连接 , 求证:平分;(2)、如图2所示,在矩形中,折叠矩形,使点 , 重合,折痕为 , 点的对应点为 , 当时,求证:四边形为“斜腰等底直角梯形”;(3)、如图3所示,在中, , , , 若以 , 为边画四边形 , 当四边形是“斜腰等底直角梯形”时,直接写出的长. -
13、综合与实践
【问题背景】杆秤是我国古代传统的度量衡三大件之一,在学习了杆秤相关知识之后,小红学习小组想利用一根木棒制作一个简易杆秤.
【制作实验】
(1)如图所示,在木棒上先确定点为杆秤提组,点A处挂托盘,选取的托盘质量 , 秤砣质量 , 测得 .
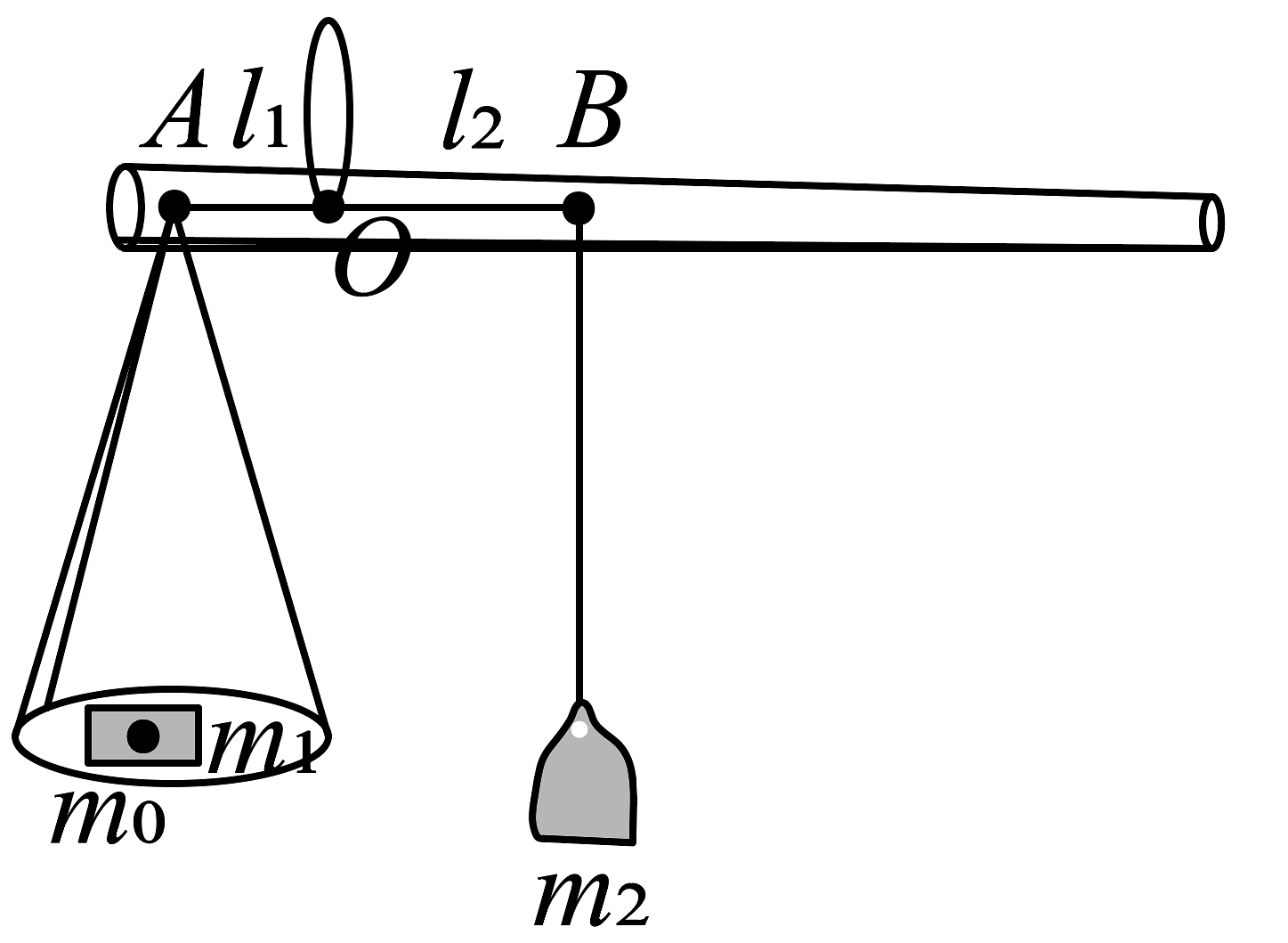
(2)先在托盘里加相应质量的物体,调整秤砣位置,使杆秤保持平衡,记录的长度,获得的实验数据如表所示:
物体质量
0
1
2
3
4
长度
1.5
4.5
7.5
10.5
13.5
任务1:杆秤在不挂重物而保持平衡时,其点所处的位置,称为定盘星.由表可知,定盘星和提纽的距离是 ▲ .
【建立模型】
任务2:小组讨论认为长度与物体质量的关系可以用一次函数来刻画.请求出长度与物体质量的函数关系式.
【结论应用】
任务3:经测量,发现该木棒在提纽挂秤砣一侧的长度为 , 根据要求,制作杆秤刻度时需在杆头和杆尾各预留长的部分用作杆秤美化,求该杆秤称量重物的最大量程.
-
14、如图,是半圆的直径,点是半圆上的一点,过点作半圆的切线交延长线于点 , 过点作于点 , 交半圆于点 .
 (1)、求证:平分;(2)、若 , , 求的长.
(1)、求证:平分;(2)、若 , , 求的长. -
15、为优化校园科技节活动设计,提升师生参与体验,某校在“智创未来”科技节结束后,随机抽取100名学生和15名教师对科技节活动进行满意度评分(满分100分).并将收集到的评分数据进行整理、描述和分析.下面给出了部分信息:

a.100名学生所评分数的频数分布直方图如图所示.数据分成4组:
① , ② , ③ , ④ .
b.15名教师所评分数为:
78,82,84,86,86,88,89,89,90,90,90,91,92,95,96.
c.100名学生和15名教师对科技节活动满意度分数的平均数、中位数、众数如表所示.
分类
平均数
中位数
众数
学生评分
89
教师评分
89
根据以上信息,回答下列问题:
(1)、的值为 , 的值位于学生评分数据分组的第组.(2)、通过计算,求表中的值.(3)、根据相关规定,满意度评定结果可划分为三个等级:低于70分为“不满意”,70分至85分为“一般”,高于85分为“满意”.根据上述师生评分,试判断本次科技节活动师生满意度评定等级,并说明你的理由. -
16、邓先生驾车从深圳宝安国际机场返回中山市博览中心.导航显示,若经过虎门大桥路程约为100公里;若经过深中通道,路程约为54公里,且比经过虎门大桥用时少36分钟.若邓先生驾车的平均车速不变,则平均车速是多少?(结果保留小数点后一位)
-
17、如图所示,为等腰直角三角形, , 点是的中点,点是上一点.
 (1)、尺规作图:用无刻度的直尺和圆规,过点作的垂线,交于点(不写作法,保留作图痕迹);(2)、在(1)的条件下,求证: .
(1)、尺规作图:用无刻度的直尺和圆规,过点作的垂线,交于点(不写作法,保留作图痕迹);(2)、在(1)的条件下,求证: . -
18、先化简,再求值: , 其中 , .
-
19、在物理实验课上,教师指导学生进行一次光的折射实验,如图所示.光线在水面点处,经折射后到盆底点处,法线与盆底交于点 . 光线的入射角为 , 折射角为 . 若规定“”为折射率 , 则光在水中的折射率约为 . 当时,测得 , 则的长为 .

-
20、如图, , , 是等边三角形,点 , , , 在同一直线上,点 , , 在同一直线上, . 若 , 则 .
