-
1、已知圆锥底面半径为2,母线长为5,则此圆锥侧面展开图的面积是 .
-
2、若关于的一元二次方程总有两个不相等的实数根,请写出一个满足条件的的值 . (写出一个即可)
-
3、已知 , 则 .
-
4、《孙子算经》是我国古代数学经典著作,书中记载了这样一道题目:今有三人共车,二车空:二人共车、九人步、人与车各几何?其意思是:今有3个人坐一辆车,有2辆车是空的;2个人坐一辆车,有9个人需要步行.人与车各多少?若设有人,车辆,则可列方程组是( )A、 B、 C、 D、
-
5、如图, , , 为的弦,连接 , , , 若 , 则下面结论不正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、生菜是一种常见的蔬菜,其生长过程分为发芽期、幼苗期、莲座期、结球期四个时期,小明记录劳动种植园的生菜生长过程,发现其中一株生菜的高近似是生长时间天的一次函数,部分数据如8表所示,则与之间的关系式为( )
生长时间/天
30
35
高度
10
15
A、 B、 C、 D、 -
7、二十四节气是中国古人订立的一种用来指导农事的补充历法,是中华民族劳动人民长期经验积累的成果和智慧的结晶.春、夏、秋、冬四季各有二十四节气中的6个.从二十四个节气中任选一个节气,这个节气在春季的概率是( )A、 B、 C、 D、
-
8、如图,在中, , 平分 , , , 则的面积是( )
 A、10 B、5 C、3 D、2
A、10 B、5 C、3 D、2 -
9、如图,点在反比例函数图象上,轴于点 , 若的面积等于3,则的值是( )
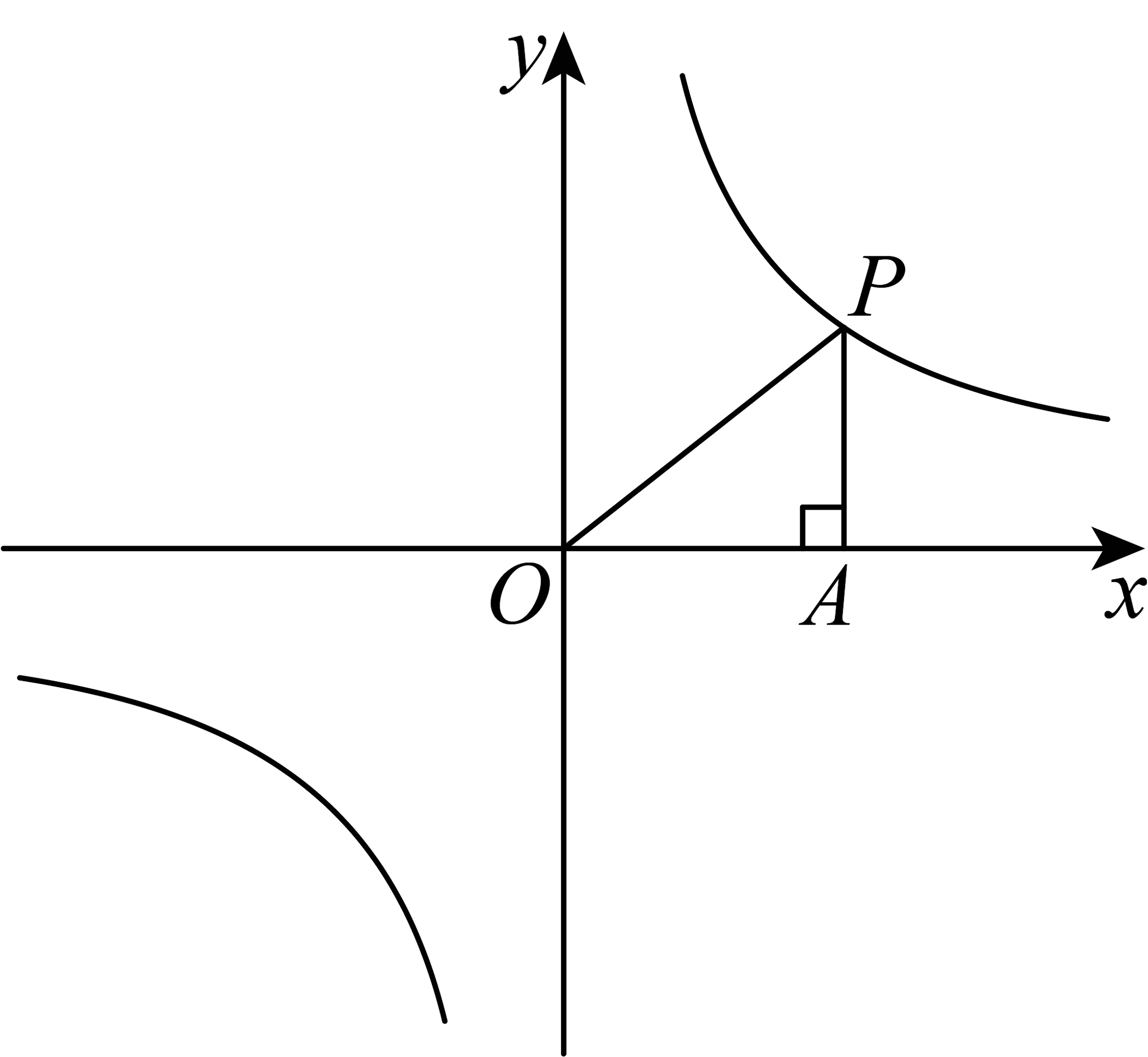 A、3 B、 C、6 D、
A、3 B、 C、6 D、 -
10、不等式的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
11、在平面直角坐标系中,点的坐标是 , 则点关于原点对称的点的坐标是( )A、 B、 C、 D、
-
12、的值是( )A、2 B、 C、4 D、
-
13、如图1,点P是对角线上的一点(),且使得 , 连接并延长,交于点E.
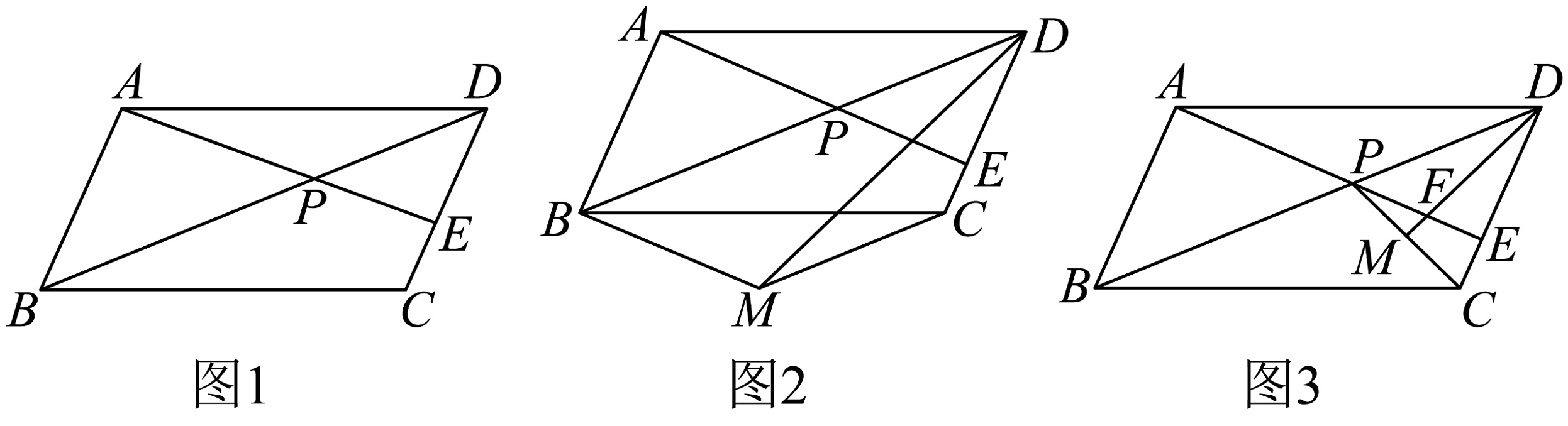 (1)、若 , 求的值.(2)、如图2,将沿方向平移到 , 求证: .(3)、如图3,连接 , 取的中点M,连接交于点F,若 , 求的值.
(1)、若 , 求的值.(2)、如图2,将沿方向平移到 , 求证: .(3)、如图3,连接 , 取的中点M,连接交于点F,若 , 求的值. -
14、综合与实践:某校七年级课外实践小组进行进位制的认识与探究活动,过程如下:
【进位制的认识】
①进位制是人们为了记数和运算方便而约定的记数系统.约定逢十进一就是十进制,逢二进一就是二进制,即“逢几进一”就是几进制,几进制的基数就是几.
②为了区分不同的进位制,常在数的右下角标明基数,例如,就是二进制数1011的简单写法.十进制数一般不标注基数.
③一个数可表示成各数位上的数字与基数的幂的乘积之和的形式.规定当时, . 如:; .
【解决问题】
(1)、我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.一位母亲在从右到左依次排列的绳子上打结,采取满七进一的方式,用来记录孩子自出生后的天数.例如图1表示的是孩子出生后30天时打绳结的情况(因为:),那么由图2可知,孩子出生后的天数是________天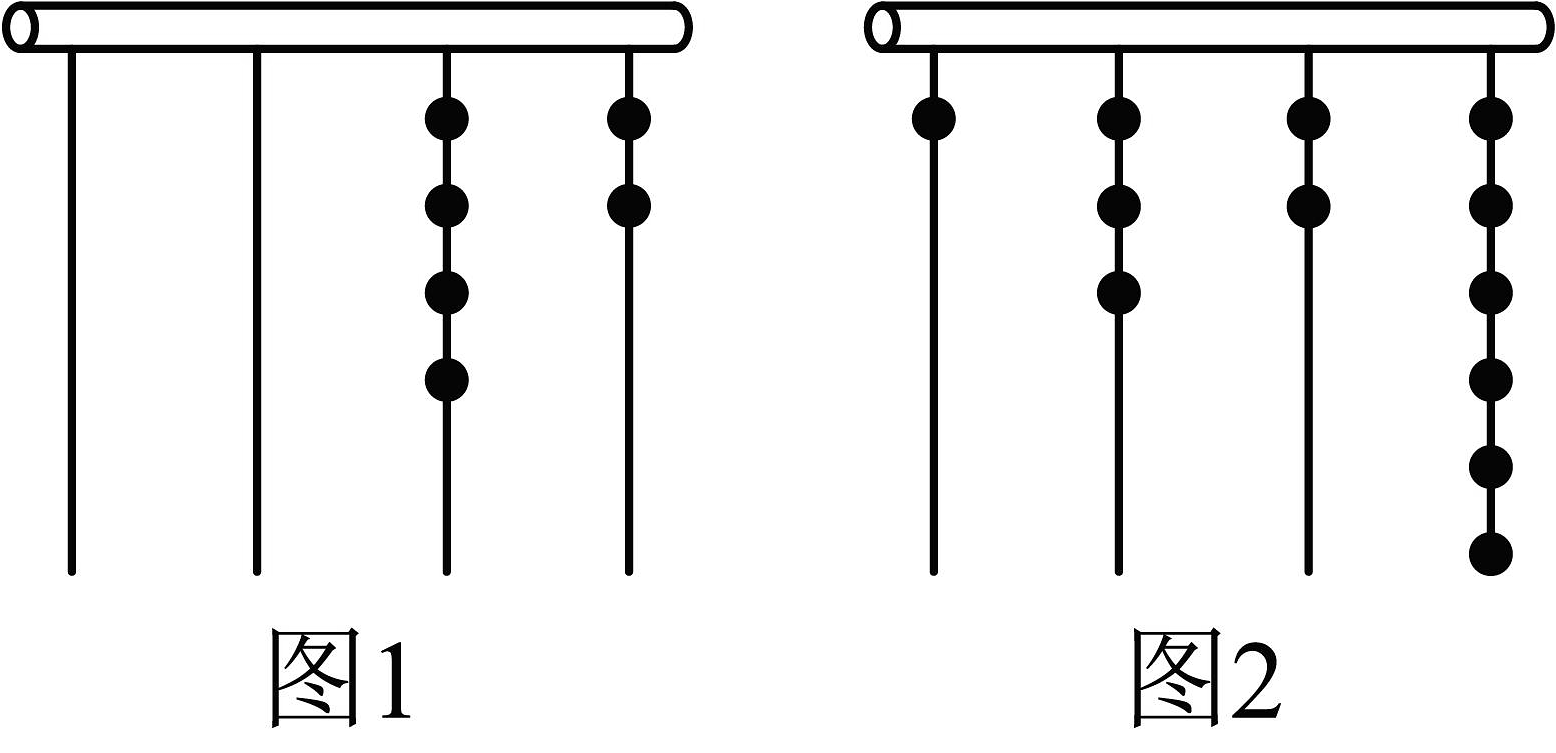 (2)、类比十进制加减法计算(结果保留二进制)
(2)、类比十进制加减法计算(结果保留二进制)例如;
写出________________
(3)、小华设计了一个n进制数265,换算成十进制数是145,求n的值(n为正整数). -
15、为了弘扬和传承中华优秀传统文化,某校举办了一场名为“经典文化传承大赛”的初赛,比赛设定满分为10分,参赛学生的得分均为整数.以下是甲、乙两组(每组10人)学生在初赛中的成绩记录(单位:分):
甲组:6,7,9,10,6,5,6,6,9,6.乙组:10,7,6,9,6,7,7,6,7,5.
(1)、根据甲、乙两组学生的成绩,得到以下的统计表:组别
平均数
中位数
众数
方差
甲组
7
a
6
2.6
乙组
7
7
b
c
(1)在以上成绩统计表中,____,____,_____.
(2)、小明同学说:“这次竞赛我得了7分,在我们小组中属于中游略偏上的水平.”根据上面的统计表,判断小明是哪个组的学生,并解释原因.(3)、从平均数和方差看,若从甲、乙两组学生中选择一个成绩较为稳定的小组参加决赛,应选哪个组?并说明理由. -
16、如图,在中, .
 (1)、用直尺和圆规在的内部作射线 , 使(不要求写作法,保留作图痕迹)(2)、若(1)中的射线交于D, , , 求长.
(1)、用直尺和圆规在的内部作射线 , 使(不要求写作法,保留作图痕迹)(2)、若(1)中的射线交于D, , , 求长. -
17、计算:
-
18、一无盖纸杯如图1所示,经测量:杯口直径 , 杯底直径 , 杯壁 . 纸杯的侧面展开示意图为环形的一部分(如图2所示,忽略拼接部分),则它所对的圆心角的度数 .

-
19、在一次1000米长跑比赛中,甲、乙两人所跑的路程y(米)随所用时间x(秒)变化的图象如图所示.根据图象信息,下列说法正确的是( )
 A、乙比甲先到达终点 B、两人相遇前,甲的速度小于乙的速度 C、甲的速度随着时间的增加而变快 D、出发后120秒,两人行程均为500米
A、乙比甲先到达终点 B、两人相遇前,甲的速度小于乙的速度 C、甲的速度随着时间的增加而变快 D、出发后120秒,两人行程均为500米 -
20、《九章算术》中有一道“甲乙持钱”问题,大意如下:甲、乙两人各有钱,但数目未知.若甲得到乙钱的一半,则甲有50钱;若乙得到甲钱的三分之二,则乙也有50钱,问甲、乙原有多少钱?设甲原有钱,乙原有钱,则( )A、 B、 C、 D、