相关试卷

1、如图，将数轴上-6与6的对应点间的线段六等分，这五个等分点所对应的数依次为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ ，则下列正确的是（）

A、 $a_{3} > 0$ B、 $| a_{1} | = | a_{4} |$ C、 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = 0$ D、 $a_{2} + a_{5} < 0$

查看解析
2、点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $\dots$ ， $A_{n}$ （ $n$ 为正整数）都在数轴上，点 $A_{1}$ 在原点 $O$ 的左边，且 $A_{1} O = 1$ ，点 $A_{2}$ 在点 $A_{1}$ 的右边，且 $A_{2} A_{1} = 2$ ，点 $A_{3}$ 在点 $A_{2}$ 的左边，且 $A_{3} A_{2} = 3$ ，点 $A_{4}$ 在点 $A_{3}$ 的右边，且 $A_{4} A_{3} = 4$ ……依照上述规律，点 $A_{2008}$ ， $A_{2009}$ 所表示的数分别为（）.

A、2008，-2009 B、-2008，2009 C、1004，-1005 D、1004，-1004

查看解析
3、如图，在数轴上A点、B点表示的数分别为a，b，AB表示A，B两点间的距离，且a，b满足|a+3|+（b+3a）²=0.点P从A点以3个单位每秒向右运动，点Q同时从B点以2个单位每秒向左运动.若AP+BQ=2PQ，则运动时间t的值为.

查看解析
4、数形相伴

(1)、如图所示，点A，B所代表的数分别为-1，2，在数轴上画出与A，B两点的距离和为5的点（并标上字母）.

(2)、若数轴上点A，B所代表的数分别为a，b，则A，B两点之间的距离可表示为AB=la-b|，那么，当|x+1|+|x-2|=7时，x=；当|x+1|+|x-2|>5时，数x所对应的点在数轴上的位置是在.

查看解析
5、纸上画有一条数轴，将纸对折后，若表示4的点与表示-1的点恰好重合，则此时与表示-3的重合的点所表示的数是.

查看解析
6、一个跳蚤在一条直线上，从0点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位···依此规律跳下去，当它跳第100次落下时，求落点处离O点的距离（用单位表示）.

查看解析
7、在数轴上任取一条长度为1999 $\frac{1}{9}$ 的线段，则此线段在这条数轴上最多能盖住的整数点的个数是（）.

A、1998 B、1999 C、2000 D、2001

查看解析
8、数轴上A，B，C三点所代表的数分别是a，1，c，且|c-1|-|a-1|=|a-c|，若下列选项中，有一个表示A，B，C三点在数轴上的位置关系，则此选项是（）

A、 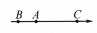B、 C、 D、

查看解析
9、如图，四个有理数在数轴上的对应点分别为M，P，N，Q.若点M，N表示的有理数互为相反数，则图中表示绝对值最小的数的点是（）

A、点M B、点N C、点P D、点Q

查看解析
10、如图所示，按下列方法将数轴的正半轴绕在一个圆（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0，1，2）上：先让原点与圆周上数字0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1，2，3，4，……所对应的点分别与圆周上1，2，0，1……所对应的点重合.这样，正半轴上的整数就与圆周上的数字建立了一种对应关系。

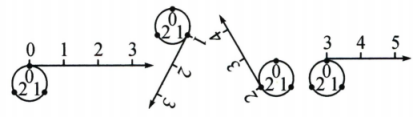(1)、圆周上的数字a与数轴上的数5对应，则а=.

(2)、数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是（用含n的代数式表示）.

查看解析
11、点A，B，C在同一条数轴上，其中点A，B表示的数分别为-3，1，若BC=2，则AC的值为.

查看解析
12、电影《哈利·波特》中，哈利·波特穿墙进人“9 $\frac{3}{4}$ 站台”的镜头（如图中的M站台），构思奇妙，给观众留下了深刻的印象.若A，B站台分别位于-2，-1处，AN＝2NB，则N站台用类似电影中的方法可称为“站台”.

查看解析
13、小涵、小敏和小灵三位同学，对小雅书包里的书的本数做出不同的估计：
小涵说：“书包里至少有10本书.”
小敏说：“不！不！书包里的书不到10本.”
小灵接着说：“书包里最少有1本书。”
这时，小雅说：“你们三个人的话，只有1个人正确。”
请问：小雅书包里有几本书?

查看解析
14、已知数轴上的点A和点B之间的距离为28个单位长度，点A在原点的左边，距离原点8个单位长度，点B在原点的右边.

(1)、求A，B两点所对应的数.

(2)、数轴上点A以每秒1个单位长度出发向左运动，同时点B以每秒3个单位长度的速度向左运动，在点C处追上了点A，求C点对应的数.

(3)、已知在数轴上点M从点A出发向右运动，速度为每秒1个单位长度，同时点N从点B出发向右运动，速度为每秒2个单位长度，设线段NO的中点为P（O为原点），在运动的过程中线段PO-AM的值是否变化？若不变，求其值；若变化，请说明理由.

查看解析
15、电子跳蚤落在数轴上的某点K。第一步从K。向左跳1个单位到K，第二步由K₁ ，向右跳2个单位到K₂ ，第三步由K₂ ，向左跳3个单位到K₃ ，第四步由K₃向右跳4个单位到K₄ ， …，按以上规律跳了100步时，电子跳蚤落在数轴上的点K₁₀₀所表示的数恰好是19.94，试求电子跳蚤的初始位置K。点所表示的数.

查看解析
16、如图，数轴上标出若干个点，每相邻两点相距1个单位，点A，B，C，D对应的数分别是整数a，b，c，d，且d-2a=10，那么数轴的原点应是（）

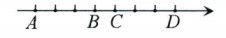A、A点 B、B点 C、C点 D、D点

查看解析
17、

(1)、已知a，b为有理数，且a>0，b<0，a+b<0，将四个数a，b，-a，-b按由小到大的顺序排列是.

(2)、已知数轴上有A，B两点，A，B之间的距离为1，点A与原点O的距离为3，那么点B对应的数是.

查看解析
18、古希腊数学家定义了五边形数，如下表所示，将点按照表中方式排列成五边形点阵，图形中的点的个数即五边形数
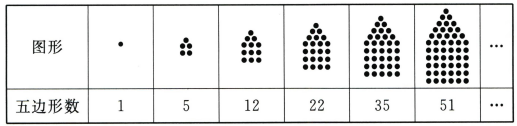
将五边形数1，5，12，22，35，51，…，排成如下数表：

观察这个数表，则这个数表中的第八行从左至右第2个数是多少?

查看解析
19、自然数按如下规律排列：

(1)、求上起第十行、左起第十三列的数.

(2)、数127 应在上起第几行、左起第几列?

查看解析
20、下面是一个按某种规律排列的数阵
根据规律，自然数2000 应该排在从上向下数的第 m 行，是该行中的从左向右数的第n个数，那么m+n的值是（）.

A、110 B、109 C、108 D、107

查看解析

上一页 890 891 892 893 894 下一页跳转