-
1、已知P=3xy-8x+1，Q=x-2xy-2，当x≠0时，3P-2Q=7恒成立，则y的值为.
-
2、按下面的程序计算，若开始输入的值为正数x，最后输出的结果为656，那么满足条件的x的不同值最多有多少个?
-
3、某人租用一辆汽车由 A 城前往 B城，沿途可能经过的城市以及通过两城市之间所需的时间(单位：小时)如图所示.若汽车行驶的平均速度为80千米/时，而汽车每行驶1千米需要的平均费用为1.2元，试指出此人从 A城出发到 B城的最短路线，并求出所需费用最少为多少元?
-
4、利用如图①的二维码可以进行身份识别.某校建立了一个身份识别系统，图②是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0.将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生 图①第11题图所在班级序号，其序号为 如图②第一行数字从左到右依次为0，1，0，1，序号为 表示该生为5班学生.以下表示6班学生的识别图案是( ).
A、
B、
C、
D、
-
5、计算机中的堆栈是一些连续的存储单元，在每个堆栈中数据的存入、取出，按照“先进后出”的原则.如图堆栈(1)的2个连续存储单元已依次存入数据b，a，取出数据的顺序是a，b；堆栈(2)的3个连续存储单元已依次存入数据e，d，c，取出数据的顺序则是c，d，e.现在要从这两个堆栈中取出这5个数据(每次取出1个数据)，则不同顺序的取法的种数有( ).
A、5 种 B、6种 C、10种 D、12种 -
6、某综合性大学拟建校园局域网络，将大学本部A 和所属专业学院B，C，D，E，F，G之间用网线连接起来.经过测算，网线费用如图所示(单位：万元)，每个数字表示对应网线(线段)的费用，实际建网时，部分网线可以省略不建，但本部及所属专业学院之间可以传递信息，那么建网所需的最少网线费用为万元.
-
7、我们知道在十进制加法中，逢十进一，如9+8=17，也可写成9(10)+8(10)=17(10)；在四进制加法中，逢四进一，如 那么在n进制中有等式 则n 的值为.
-
8、为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密).已知有一种密码，将英文26个小写字母a，b，c，…，z依次对应0，1，2，3，…，25这26个自然数(如下表).当明文中的字母对应的序号为β时，将β+10除以26后所得的余数作为密文中的字母对应的序号，例如明文s对应密文c.
字母
a
b
c
d
e
f
g
h
i
j
k
1
m
序号
0
1
2
3
4
5
6
7
8
9
10
11
12
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
13
14
15
16
17
18
19
20
21
22
23
24
25
按上述规定，将明文“maths”译成密文.
-
9、生活中常用的十进制是用0~9这十个数字来表示数，满十进一，例：12=1×10+2，212=2×10×10+1×10+2；计算机也常用十六进制来表示字符代码，它是用0~F来表示0~15，满十六进一，它与十进制对应的数如下表：
十进制
0
1
2
…
8
9
10
11
12
13
14
15
16
17
…
十六进制
0
1
2
…
8
9
A
B
C
D
E
F
10
11
例：十六进制2B对应十进制的数为2×16+11=43，10C对应十进制的数为1×16×16+0×16+12=268，那么十六进制中14E对应十进制的数为( )
A、28 B、62 C、238 D、334 -
10、如图所示的运算程序中，若开始输入的x 值为48，我们发现第一次输出的结果为24，第二次输出的结果为12……则第2010 次输出的结果为( ).
A、6 B、3 C、 D、 -
11、在计算机程序中，二叉树是一种表示数据结构的方法.如图，一层二叉树的结点总数为1，二层二叉树的结点总数为3，三层二叉树的结点总数为7……照此规律，七层二叉树的结点总数为( ).
A、63 B、64 C、127 D、128 -
12、条码信息
细心的朋友会发现：超市里的每一件商品的包装盒(袋)上都印有条形码.每个条形码表示一个13位数.现有示意图表示：
前面3位是国际物品编码协会分配给该国物品编码中心的号码，它代表生产国家，接下来的5位代表生产企业，再接下来的4位代表商品名称，最后1位是校验码.条形码的13位数符合这样的规则：将(左起)偶数位上数的和乘3后，与奇数位上数的和相加，总和为10的倍数.比如一个商品条形码为690909500151x，其中x表示待求的校验码，则x=.
-
13、太极八卦
八卦是中国古代道家论述万物变化的经典著作《周易》中的8种基本图形，由符号“———”和“——”组成(如图).
现代计算机采用的数制是二进制，其主要原因在于，可以分别用二进制中的“1”和“0”来表示电路的“通”“断”两种状态.
德国数学家莱布尼茨发明了二进制，他认为，世界上最早的二进制表示法就是中国的八卦(“——”和“———”分别表示1 和0).
填写下面关于八卦与二进制关系的表：
数与代数
-
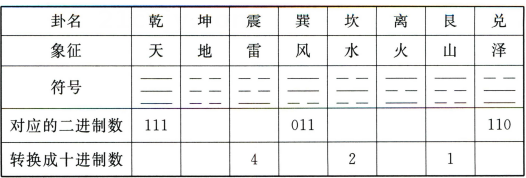
14、先阅读下面的材料，再解答后面各题.
现代社会对保密要求越来越高，密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解，其中 Q，W，E，…，N，M这26个字母依次对应1，2，3，…，25，26这26个正整数(见下表)：
Q
W
E
R
T
Y
U
I
O
P
A
S
D
1
2
3
4
5
6
7
8
9
10
11
12
13
F
G
H
J
K
L
Z
x
C
V
B
N
M
14
15
16
17
18
19
20
21
22
23
24
25
26
给出一个变换公式：
，
将明文转换成密文，如：
即R变为L；
即 A变为S.
将密文转换成明文，如：
21→3×(21-17)-2=10，即X变为 P；
13→3×(13-8)-1=14，即D变为 F.
(1)、按上述方法将明文 NET 译为密文.(2)、若按上述方法将明文译成的密文为DWN，请找出它的明文. -
15、图中的程序表示，输入一个整数便会按程序进行计算.
设输入的x值为18，那么根据程序，第1次计算的结果是9，第2次计算的结果是4……这样下去第5次计算的结果为；第2009次计算的结果是.
-
16、你觉得手机很神奇吗?它能在瞬间清晰地传递声音、文字、图像等信号，据说以后还能发送味道、触觉信息呢！这里都有手机中电脑芯片的功劳.其实，这些信号在电脑芯片中都是以二进制数的形式给出的.每个二进制数都由0 和1构成，电脑芯片上电子元件的“开”“关”分别代表“1”和“0”.一组电子元件的“开”“关”状态就表示相应的二进制数. 例如“开”“开”“关”表示“110”.
如图，电脑芯片的某段电路上分布着一组电子元件(假设它们首尾不相连)，且相邻的两个元件不能同时是关的(以下各小题要求写出解答过程).
(1)、若此电路上有4个元件，则这4个元件所有不同的“开”“关”状态共有多少种?(请一一列出)(2)、若用aₖ表示电路上k(k≥1)个电子元件所有不同的“开”“关”状态数，试探索ak， ak+1， ak+2之间的关系式(不要求论证).(3)、试用(2)中探索出的递推关系式，计算a10的值. -
17、计算机利用的是二进制数，它共有两个数码0，1，将一个十进制数转化为二进制数，只需把该数写成若干个2”数的和，依次写出1或0即可.如
为二进制下的5位数，则十进制数2004是二进制下的( ).
A、10位数 B、11位数 C、12位数 D、13位数 -
18、如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连.连线标注的数字表示该段网络单位时间内可以通过的最大信息量.现从结点 A 向结点 B传递信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为.
-
19、在“□1□2□3□4□5□6□7□8□9”的小方格中填上“+”“一”号，如果可以使其代数和为n，就称数n是“可被表出的数”（如1是可被表出的数，+1+2-3-4+5+6-7--8+9是1的一种可被表出的方法）.(1)、求证：7是可被表出的数，而8是不可被表出的数.(2)、求25可被表出的不同方法的种数.
-
20、 形数(1)、古希腊人常用小石子在沙滩上摆成各种形态来研究数.比如：他们研究过图①中的1，3，6，10，…，由于这些数能够表示成三角形，故将其称为三角形数.类似地，图②中的1，4，9，16，…，这样的数被称为正方形数.下列数中，既是三角形数，又是正方形数的是（ ）.A、289 B、1024 C、1225 D、1378
(2)、古希腊数学家把数1，3，6，10，15，21，…叫作三角形数，它有一定的规律性，若把第一个三角形数记为a1 ， 第二个三角形数记为a2……第n个三角形数记为 an，则有 a3 ， a3+a4 ， …，请求出a399+a400的值.