相关试卷

1、已知关于x的一元二次方程（m²-4）x²+2（m-2）x+1=0有实数根，当m取最大整数值时，代数式3x²+2x+3的值为.

查看解析
2、如图，将平行四边形ABCD折叠，使点C落在AD边上的点C'处，若∠1=58°，∠2=42°，则∠C的度数为.

查看解析
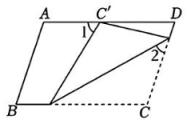
3、已知一个n边形的内角和是900°，则n=.

查看解析
4、要使二次根式 $\sqrt{x - 2025}$ 在实数范围内有意义，则x的取值范围是.

查看解析
5、如图，正方形ABCD中，点E、H、G、F分别为AB、BC、CD、AD边上的点，点K、M、N为对角线BD上的点，四边形EKNF和四边形MHCG均为正方形，它们的面积分别表示为 $S_{1}$ 和 $S_{2}$ ，给出下面三个结论：① $S_{1} = S_{2}$ ；② $D F = 2 A F$ ；③ $S_{正方形 A B C D} = \frac{9}{4} S_{1} + 2 S_{2}$ .上述结论中，所有正确结论的序号是（）

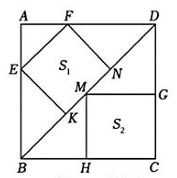A、② B、①③ C、②③ D、①②③

查看解析
6、如图，在 $R t △ A B C$ 中 $∠ C = 9 0^{°}$ ，点D在AC边上， $A D = B C$ ，点E是CD的中点，点F是AB的中点，若 $A D = 2$ ，则EF的长为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\frac{3}{2}$

查看解析
7、如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图像与反比例函数 $y_{2} = \frac{m}{x}$ （m为常数且 $m \neq 0$ ）的图像都经过A（-1，2），B（2，-1），结合图像，则不等式 $k x > \frac{m}{x} - b$ 的解集是（）

A、 $x < - 1$ B、 $- 1 < x < 0$ C、 $x < - 1$ 或 $0 < x < 2$ D、 $- 1 < x < 2$

查看解析
8、某种植物只有一个主干，该主干上长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是111，设一个主干长出x个支干，则下列方程中正确的是（）

A、1+x²=111 B、（1+x）²=111 C、1+x+x²=111 D、1+（1+x）+（1+x）²=111

查看解析
9、命题“在同一平面内，若a//b，a//c，则b//c”，用反证法证明，应假设（）

A、a⊥c B、b⊥c C、a与c相交 D、b与c相交

查看解析
10、下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
11、如图，在矩形ABCD中，DE平分∠ADC交BC于E，连结AE，DE.

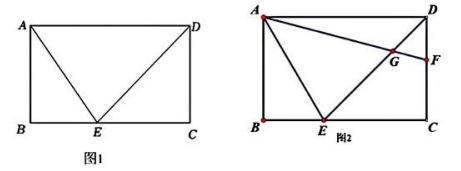(1)、如图1，若AB=3，AD=5，求AE的长；

(2)、如图2，若点F是DC边上的一点，若CF=BE，连结AF交DE于G，
①猜想∠EAF的度数，并说明理由；
②若 $D G = D F$ ，求 $\frac{D F}{A D}$ 的值.

查看解析
12、综合与实践：如图1，某兴趣小组计划开垦一个面积为8m²的矩形地块ABCD种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为am·
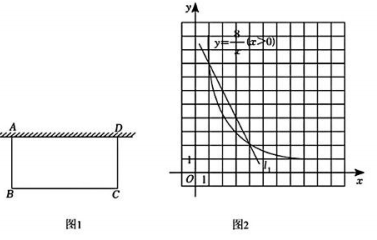
【问题提出】：小组同学提出这样一个问题：若a=10，能否围出矩形地块？

(1)、【问题探究】：小颖尝试从“函数图象”的角度解决这个问题：
设AB为xm，BC为ym．由矩形地块面积为 $8 m^{2}$ ，得到 $x y = 8$ ，满足条件的 $(x, y)$ 可看成是反比例函数 $y = \frac{8}{x}$ 的图象在第一象限内点的坐标；木栏总长为10m，得到 $2 x + y = 10$ ，满足条件的 $(x, y)$ 可看成一次函数 $y = - 2 x + 10$ 的图象在第一象限内点的坐标，同时满足这两个条件的 $(x, y)$ 就可以看成两个函数图象交点的坐标．
如图2，反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象与直线 $l_{1} : y = - 2 x + 10$ 的交点坐标为 $(1, 8)$ 和，因此，木栏总长为10m时，能围出矩形地块，分别为： $A B = 1 m, B C = 8 m$ ；或 $A B =$ $m, B C =$ $m$ ．
根据小颖的分析思路，完成上面的填空；

(2)、【类比探究】
若 $a = 6$ ，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由；

(3)、【问题延伸】
当木栏总长为am时，小颖建立了一次函数 $y = - 2 x + a$ ．发现直线 $y = - 2 x + a$ 可以看成是直线 $y = - 2 x$ 通过平移得到的，在平移过程中，当过点 $(2, 4)$ 时，直线 $y = - 2 x + a$ 与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象有唯一交点．请在图2中画出直线 $y = - 2 x + a$ 过点 $(2, 4)$ 时的图象，并求出 $a$ 的值；

(4)、【拓展应用】：小颖从以上探究中发现＂能否围成矩形地块问题＂可以转化为＂ $y = - 2 x + a$ 与 $y = \frac{8}{x}$ 图象在第一象限内交点的存在问题＂．
若要围出满足条件的矩形地块，且AB和BC的长均不小于1m，请直接写出 $a$ 的取值范围．

查看解析
13、如图，已知正方形ABCD的边长为12，点E在DC边上，点G在BC的延长线上，设正方形CEFG的面积为 $S_{1}$ ，以线段AD和DE为邻边的矩形的面积为 $S_{2}$ ，且 $S_{1} = \frac{4}{3} S_{2}$ .

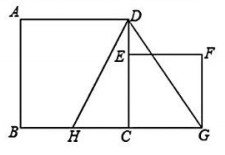(1)、求线段DE的长.

(2)、若H为BC边上一点， $C H = 5$ ，连接DH，DG，判断 $△ D H G$ 的形状.

查看解析
14、在平面直角坐标系中，正比例函数 $y_{1} = a x (a \neq 0)$ 与反比例函数 $y_{2} = \frac{k}{x} (k \neq 0)$ 的图象交于A，B两点，其中点A（2，3）.

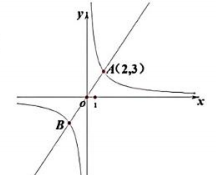(1)、求a，k的值；

(2)、y轴上有一点C，满足 $△ A B C$ 的面积为8，求点C坐标.

查看解析
15、如图，已知在AABC中，D为BC的中点，连接AD，E为AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF.

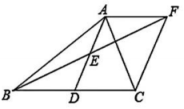(1)、求证：四边形ADCF为平行四边形.

(2)、当AB=AC时，求证：四边形ADCF是矩形.

查看解析
16、在一次体操比赛中，6个裁判员对某一运动员的打分数据（动作完成分）如下：
9.68.88.88.98.68.7
对打分数据有以下两种处理方式：
方式一：不去掉任何数据，用6个原始数据进行统计；
平均分
中位数
方差
89
a
0.107
方式二：去掉一个最高分和一个最低分，用剩余的4个数据进行统计：
平均分
中位数
方差
b
8.8
c

(1)、a= ， b= ， c=；

(2)、你认为把哪种方式统计出的平均分作为该运动员的最终得分更合理？写出你的判定并说明理由.

查看解析
17、

(1)、计算： $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{24} \div \sqrt{3}$ ；

(2)、解方程： $x^{2} - 2 x = 2 x + 1$ .

查看解析
18、如图，在菱形纸片ABCD中， $∠ A = 6 0^{°}$ ，将纸片折叠，点A、D分别落在 $A' 、 D'$ 处，且 $A^{'} D^{'}$ 经过点B，EF为折痕，当 $D' F ⊥ C D$ 时，此时 $∠ B E F =$ °； $\frac{C G}{B G} =$ ．

查看解析
19、如图，正方形ABCD中，分别取AD和CD边的中点E，F，连接BE，AF相交于点 $G$ ，连接CG，若 $∠ A E B = α$ ，则 $∠ B C G$ 的度数为．

查看解析
20、若二次根式 $\sqrt{1 - 2 a}$ 有意义，则 $a$ 的取值范围是．

查看解析

上一页 1045 1046 1047 1048 1049 下一页跳转

平均分	中位数	方差
89	a	0.107

平均分	中位数	方差
b	8.8	c