相关试卷

1、要使分式 $\frac{x - 1}{x - 2}$ 有意义，则的取值范围是.

查看解析
2、已知a=m+2024，b=m+2025，c=m+2026，则代数式a²+b²+c²-ab-bc-ac的值为（）

A、5 B、6 C、3 D、8

查看解析
3、若关于x的分式方程 $\frac{m}{x - 1} - \frac{2}{1 - x} = 1$ 的解为正数，则m的取值范围是（）

A、 $m > - 3$ B、 $m \neq 1$ C、 $m > - 3$ 且 $m \neq - 2$ D、 $m > - 3$ 且 $m \neq 1$

查看解析
4、如果 $(x^{2} + p x + q) (x^{2} - 3 x + 2)$ 的展开式中不含 $x^{2}$ 项和x项，则p，q的值分别为（）

A、 $p = 0$ ， $q = 0$ B、 $p = - 3$ ， $q = - 9$ C、 $p = \frac{6}{7}$ ， $q = \frac{4}{7}$ D、 $p = - 3$ ， $q = 1$

查看解析
5、古代数学趣题：老头提篮去赶集，一共花去七十七；满满装了一菜篮，十斤大肉三斤鱼；买好未曾问单价，只因回家心里急；道旁行人告诉他，九斤肉钱五斤鱼.意思是：77元钱共买了10斤肉和 $3$ 斤鱼， $9$ 斤肉的钱等于 $5$ 斤鱼的钱，问每斤肉和鱼各是多少钱？设每斤肉 $x$ 元，每斤鱼 $y$ 元，可列方程组为（）

A、 ${\begin{array}{l} 10 x + 3 y = 77 \\ 9 x = 5 y \end{array}$ B、 ${\begin{array}{l} 3 x + 10 y = 77 \\ 9 x = 5 y \end{array}$ C、 ${\begin{array}{l} 10 x + 3 y = 77 \\ 5 x = 9 y \end{array}$ D、 ${\begin{array}{l} 3 x + 10 y = 77 \\ 5 x = 9 y \end{array}$

查看解析
6、若 $a = - 2^{2}$ ， $b = {(- 2)}^{- 2}$ ， $c = {(- \frac{1}{2})}^{0}$ ，则（）

A、 $b < a < c$ B、 $b < c < a$ C、 $a < c < b$ D、 $a < b < c$

查看解析
7、如果分式 $\frac{x y}{2 x - 3 y}$ 中的x，y都扩大为原来的2倍，那么分式的值（）

A、不变 B、扩大为原来的2倍 C、缩小为原来的4倍 D、缩小为原来的 $\frac{1}{2}$ 倍

查看解析
8、光从空气斜射入水中，传播方向会发生变化，如图，表示水面的直线AB与表示水底的直线CD平行，光线EF从空气射入水中，改变方向后射到水底G处，FH是EF的延长线，若∠1=42°，∠2=16°，则∠CGF的度数是（）

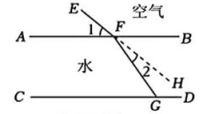A、58° B、48° C、26° D、32°

查看解析
9、下列从左到右的变形，是分解因式的是（）

A、 $3 a^{2} b^{2} = 3 a b \cdot a b$ B、 $x^{2} + x - 3 = x (x + 1) - 3$ C、 $(a + 3) (a - 3) = a^{2} - 9$ D、 $2 a^{2} + 4 a = 2 a (a + 2)$

查看解析
10、下列计算正确的是（）

A、 $x^{6} \div x^{2} = x^{3}$ B、 $(- x y^{3})^{2} = x^{2} y^{6}$ C、 $(x + y)^{2} = x^{2} + y^{2}$ D、 $(- 2 x + 1) (- 2 x - 1) = 2 x^{2} - 1$

查看解析
11、太空中微波理论上可以在0.000006秒内接收到相距约2km的信息，数据0.000006用科学记数法表示应为（）

A、 $0.6 \times 1 0^{- 7}$ B、 $0.6 \times 1 0^{- 6}$ C、 $6 \times 1 0^{- 6}$ D、 $6 \times 1 0^{- 7}$

查看解析
12、已知，A-B-E-C-D是一条折线段，且AB//CD，点E为平行线间一点.

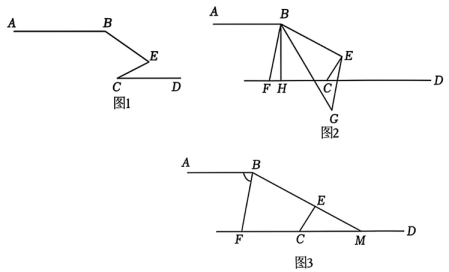(1)、如图1，若∠ABE=140°，∠ECD=25°，求∠BEC的度数；

(2)、如图2，∠ABE的角平分线交直线CD于点F，过点B作BH⊥CD于点H，过点E作EG//BF交∠HBE的角平分线于点G.若点E是位于线段BH右侧的一动点，试判断∠G是否为定值，如果是定值，请求出这个定值；如果不是，请说明理由；

(3)、如图3，点F仍满足（2）问中的条件，射线BE交直线CD于点M，若∠BMF为30°，点P为射线MF上一动点，连接EP，∠EPF的角平分线交直线BF于点O.设∠BEP=α，∠FQP=β，请直接写出α与β的数量关系.

查看解析
13、我们把形如 $x + \frac{m n}{x} = m + n$ （m，n不为零），且两个解分别为 $x_{1} = m$ ， $x_{2} = n$ 的方程称为“十字分式方程”.例如 $x + \frac{6}{x} = 5$ 为十字分式方程，可化为 $x + \frac{2 \times 3}{x} = 2 + 3$ ， $∴ x_{1} = 2$ ， $x_{2} = 3$ ；
再如 $x + \frac{7}{x} = - 8$ 为十字分式方程，可化为 $x + \frac{(- 1) \times (- 7)}{x} = (- 1) + (- 7)$ ， $∴ x_{1} = - 1$ ， $x_{2} = - 7$ .应用上面的结论解答下列问题：

(1)、若 $x + \frac{3}{x} = 4$ 为十字分式方程，则 $x_{1} =$ ， $x_{2} =$ .

(2)、若十字分式方程 $x - \frac{2}{x} = - 3$ 的两个解分别为 $x_{1} = a$ ， $x_{2} = b$ ，求 $\frac{b}{a} + \frac{a}{b} + 1$ 的值.

(3)、若关于x的十字分式方程 $x - \frac{2025 k - 2024 k^{2}}{x - 1} = 2025 k - 2024$ 的两个解分别为 $x_{1}$ ， $x_{2}$ （ $k > 2$ ， $x_{1} > x_{2}$ ），求 $\frac{x_{1} + 4048}{x_{2}}$ 的值.

查看解析
14、如图，点D，E分别在△ABC的边AB，AC上，点F在线段BE上，且∠EDF=∠C，DE//BC.

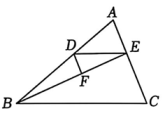(1)、判断DF与AC的位置关系，并说明理由；

(2)、若DF平分∠BDE，∠ADE=38°，求∠AED.

查看解析
15、为加强中学生的法治观念，增强法治教育，某校开展了“法治知识知多少”的调查活动，随机抽取了部分学生，对他们进行法治知识问答的小测验，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：

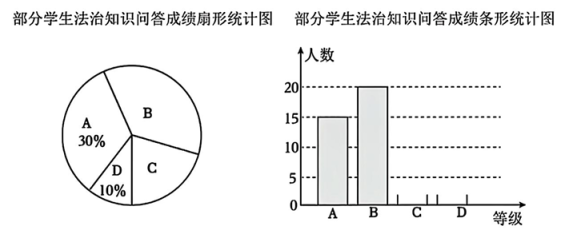(1)、本次参加调查的人数为 ▲ 人，并将条形统计图补充完整；

(2)、在扇形统计图中，等级C对应的圆心角的度数为度；

(3)、若规定达到A、B等级为优秀，该校共有学生650人，请通过样本估计该校法治知识水平达到优秀标准的学生人数.

查看解析
16、先化简再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，其中x是从0，1，2当中选一个合适的值.

查看解析
17、计算

(1)、 $a^{2} \cdot a^{4} - (- 2 a^{3})^{2}$

(2)、 $(a + b)^{2} - (a - b)^{2}$

查看解析
18、如图，长方形ABCD的边 $B C = 13$ ， E是边BC上的一点，且 $B E = B A = 10$ ， F，G分别是线段AB，CD上的动点，且 $B F = D G$ ，现以BE，BF为边作长方形BEHF，以DG为边作正方形DGIJ，点H，I均在长方形ABCD内部.记图中的阴影部分面积分别为 $S_{1}, S_{2}$ ，长方形BEHF和正方形DGIJ的重叠部分是四边形KILH，当四边形KILH的邻边比为3：4时， $S_{1} + S_{2}$ 的值为.

查看解析
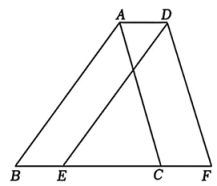
19、如图，将周长为8cm的三角形ABC沿着BC方向平移2cm，得到三角形DEF，则四边形ABFD的周长为cm.

查看解析
20、已知二元一次方程 $x - 2 y + 1 = 0$ ，用含y的代数式表示x，则 $x =$ .

查看解析

上一页 1047 1048 1049 1050 1051 下一页跳转