相关试卷

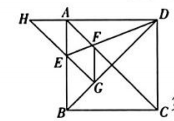1、如图，正方形ABCD的边长为1，AC，BD是对角线，将 $△ D C B$ 绕着点D顺时针旋转 $4 5^{°}$ 得到 $△ D G H$ ， HG交AB于点E，连接DE交AC于点F，连接FG，则下列结论：①四边形AEGF是菱形；② $△ H E D$ 的面积是 $1 - \frac{\sqrt{2}}{2}$ ；③ $∠ A F G = 112 . 5^{°}$ ；④ $B C + F G = \sqrt{2}$ .其中正确的结论是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看解析
2、如图，平行四边形ABCD中，点M在边AD上，以BM为折痕，将△ABM向上翻折，点A正好落在CD上的点N处.若△DMN的周长为7，△NCB的周长为13，则NC的长为（）

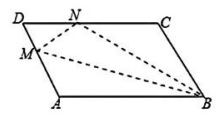A、3 B、4 C、5 D、无法确定

查看解析
3、已知，点P（a，b）在反比例函数y=- $\frac{6}{x}$ 的图象上，则下列结论正确的是（）

A、y随x的增大而增大 B、y随x的增大而减小 C、当a>-1时，则b>6 D、当a<-1时，则0<b<6

查看解析
4、阅读材料：物理学中“力的合成”遵循平行四边形法则，即F₁和F₂的合力是以这两个力为邻边构成的平行四边形的对角线所表示的力F，如下图。
解决问题：设两个共点的合力为F，现保持两力的夹角θ（0°<θ<90°）不变，使得其中一个力增大，则（）

A、合力F一定增大 B、合力F的大小可能不变 C、合力F可能增大，也可能减小 D、合力F一定减小

查看解析
5、关于x的一元二次方程x²+x-2=m，下列说法正确的是（）

A、当m=0时，此方程有两个相等的实数根 B、当m<0时，此方程没有实数根 C、当m>0时，此方程有两个不相等的实数根 D、此方程的根的情况与m的值无关

查看解析
6、小明根据演讲比赛中九位评委所给的分数制作了如下表格：
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果要去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（）

A、中位数 B、众数 C、方差 D、平均数

查看解析
7、正六边形的每个内角为（）

A、108° B、135° C、120° D、140°

查看解析
8、下列计算正确的是（）

A、 $\sqrt{(- 2)^{2}} = \pm 2$ B、 $\sqrt{(- 2)^{2}} = - 2$ C、 $\sqrt{2^{2}} = \pm 2$ D、 $\sqrt{2^{2}} = 2$

查看解析
9、已知 $t = \frac{b x + 2}{x - a}$ （a，b是常数， $x \neq a$ ）①

(1)、若 $a = - 4$ ， $b = \frac{1}{2}$ ，求 $t$ ；

(2)、试将等式①变形成“ $A x = B$ ”形式，其中A，B表示关于a，b，t的整式；

(3)、若 $t$ 的取值与x无关，试求a与b的数量关系.

查看解析
10、数学活动课上，老师准备了图1中三种不同大小的正方形与长方形卡片如图1依次记A、B、C三类，拼成了一个如图2所示的正方形

(1)、根据用两种不同的方法表示图2中正方形的面积，直接写出一个因式分解的等式.

(2)、若要拼出一个面积为（a+2b）（3a+4b）的矩形，则需要A类卡片张，B类卡片张，C类卡片张。

(3)、根据（1）题中的等量关系，解决如下问题：
①已知m+n=5，m²+n²=20，求mn和（m-n）²的值.
②已知（x-2023）²+（x-2025）²=34，求x-2024.

(4)、如图3，用三张边长为x的正方形纸片，五张长为x，宽为1的长方形纸片和两张边长为1的正方形纸片。试一试，能否把这些纸片拼成一个长方形，若能，求出新长方形的长和宽。

查看解析
11、在纸盒制作的劳动实践课上，对规格是150cm×90cm的原材料板材进行裁剪得到A型长方形纸板和B型正方形纸板.为了避免材料浪费，每张原材料板材先裁得3张150cm×30cm的纸板条，每张纸板条又恰好可以裁得3张A型长方形纸板或5张B型正方形纸板，如图1所示.（单位：cm）

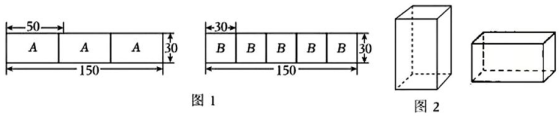(1)、每张原材料板材可以裁得A型纸板张或裁得B型纸板张：

(2)、现有260张原材料板材全部裁剪（每张原材料板材只能一种裁法）得到A型与B型纸板当侧面和底面，做成如图2所示的竖式无盖长方体纸盒和横式无盖长方体纸盒，若横式无盖长方体纸盒个数为竖式无盖长方体纸盒个数的两倍，问：怎样裁剪才能使剪出的A，B型纸板恰好用完，两种纸盒各做多少个？

查看解析
12、如图已知，∠DEC=90°，∠AGF=∠ABC，∠1与∠2互补试判断BF与AC的位置关系，并说明理由

查看解析
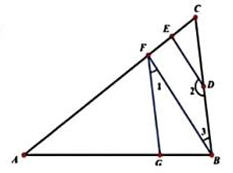
13、如图，方格纸中每个小正方形的边长都为1、三角形ABC的顶点均在方格纸的格点上，将三角形ABC平移后得到三角形A'B'C'，使点A落在直线I上的点A'处

(1)、画出平移后的三角形A'B'C'；

(2)、请描述这个平移过程.

(3)、在直线I上找一格点D，使A'，B'，C'、D所围成的四边形的面积为6.

查看解析
14、先化简，再求值： $\frac{4}{a^{2} - 4} - \frac{1}{a - 2}$ ，其中 $a = - 1$ .
小聪解答过程如下，请指出其中错误步骤的序号，并写出正确的解答过程.
原式= $\frac{4}{a^{2} - 4} \cdot (a^{2} - 4) - \frac{1}{a - 2} \cdot (a^{2} - 4)$    ①
=4-（a+2）   ②
=2-a   ③
当a=-1时，原式=2-（-1）=3

查看解析
15、解方程（组）：

(1)、 $\frac{x}{x - 2} = \frac{x + 1}{x - 2} - 1$ ；

(2)、 ${\begin{array}{l} 3 x - y = 15 \\ 5 x + 2 y = 14 \end{array}$ .

查看解析
16、将下列各式因式分解：

(1)、 $5 x^{2} - 10 x + 5$

(2)、 $(a + b)^{2} - a - b$

查看解析
17、已知关于x、y的二元一次方程组 ${\begin{array}{l} x + 2 y = 5 p \\ 2 x + y = 4 p + 3 \end{array}$ （p为实数）

(1)、x+y=（用含p的式子表示）；

(2)、若方程组的解也是方程qx+3y=1（q为整数，且q不等于0或-6）的解，p也是整数，则q的最小值为.

查看解析
18、若关于x的分式方程 $\frac{m x}{x - 1} = \frac{2}{x - 1} - 1$ 有增根，则m的值为.

查看解析
19、如图，DA//BC//EF，CE平分∠BCF，∠DAC=125°，∠ACF=15°，则∠FEC的度数是.

查看解析
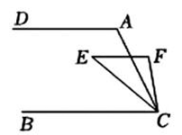
20、分解因式： $4 x^{3} y - 16 x y^{3} =$ .

查看解析

上一页 1046 1047 1048 1049 1050 下一页跳转

平均数	中位数	众数	方差
8.5	8.3	8.1	0.15