相关试卷

1、如果3^m=4，3ⁿ=5，那么3^m^-n=.

查看解析
2、已知方程3x-y=5，用含y的代数式表示下x，则x=.

查看解析
3、如图，有三张正方形纸片A，B，C，它们的边长分别为a，b，c，将三张纸片按图1，图2两种不同方式放置于同一长方形中，记图1中阴影部分周长为 $l_{1}$ ，面积为 $S_{1}$ ，图2中阴影部分周长为 $l_{2}$ ，面积为 $S_{2}$ .若 $4 (S_{2} - S_{1}) = (l_{1} - l_{2})^{2}$ ，则c：b的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看解析
4、已知分式 $\frac{3 x - n}{x + m}$ （m，n为常数）满足表格中的信息，则下列结论中错误的是（）
x的取值
-2
2
a
0
分式的值
无意义
0
1
b

A、m=2 B、n=6 C、a=-4 D、b=-3

查看解析
5、如果某个二元一次方程组的解中两个未知数的值是互为相反数，我们称这个方程组为“关联方程组”.若关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ 是“关联方程组”，则a的值为（）

A、0 B、1 C、2 D、-2

查看解析
6、图1为我国高铁座位的实物图，图2是它的简易图，座位AD和座椅靠背AE的夹角∠DAE=105°，小桌板BC与座位AD平行，小桌板支撑杆AB与桌面BC的夹角∠ABC=125°，则座椅靠背AE与小桌板支撑杆AB形成的夹角∠EAB的度数是（）

A、10° B、15° C、20° D、25°

查看解析
7、已知多项式a²+ma+n可因式分解为（a-4）（a+5），则m的值为（）

A、1 B、-1 C、-9 D、9

查看解析
8、若分式 $\frac{2 x^{2}}{3 x - 2 y}$ 中x，y的值同时扩大为原来的2倍，则分式的值（）

A、不变 B、扩大为原来的2倍 C、扩大为原来的4倍 D、不能确定解答：

查看解析
9、下列运算正确的是（）

A、 $2 a + 3 a = 5 a^{2}$ B、 $(2 x^{2})^{3} = 6 x^{6}$ C、 $x^{4} \cdot x^{2} = x^{6}$ D、 $(a - b)^{2} = a^{2} - b^{2}$

查看解析
10、若 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 关于x，y的二元一次方程 $a x - y = 1$ 的解，则a的值为（）

A、2 B、1 C、-1 D、-2

查看解析
11、在2025年蛇年春晚上，一群会跳舞、能抛手绢的人形机器人惊艳亮相，机器人的研发也成为当今时代科研的重点.中国科学院研发出新型的工业纳米机器人，其大小约为70nm.已知1nm=10^-9m，则70nm用科学记数法表示为（）

A、 $70 \times 1 0^{- 9} m$ B、 $0.7 \times 1 0^{- 7} m$ C、 $7 \times 1 0^{- 8} m$ D、 $- 7 \times 1 0^{8} m$

查看解析
12、在下面右侧的四个图形中，能由左图经过平移得到的图形是（）

A、 B、 C、 D、

查看解析
13、如图，P是矩形ABCD边BC上一动点，△ABP沿AP翻折得△AEP，直线PE交线段AD于点F，以AP，PF为边构造□APFG.

(1)、当点E在矩形ABCD内部时，
①小聪通过画图探究，得到以下数据，根据题意，将表格补充完整
∠BAP
10°
20°
40°
∠G
80°
70°
▲
∠GAF
20°
40°
▲
②写出∠G与∠GAF的数量关系，不必说明理由，

(2)、若AB=4，AD=9，AG=5，求所有符合条件的CP的长.

(3)、当点B关于AE的对称点恰好落在线段GF上，且不与点G重合时，直接写出此时的 $\frac{A E}{P F}$ 值.

查看解析
14、某兴趣小组利用代数推理方法发现了反比例函数 $y = \frac{a}{x} (a \neq 0)$ 一个有趣的结论.
小龙：如图1，直线 $y = x$ 与双曲线 $y = \frac{6}{x}$ 交于A，B两点，根据中心对称性可以得到 $O A = O B$ .

(1)、【轻松探究】直线 $y = 3 x - 4$ 与双曲线 $y = \frac{6}{x}$ 交于A，B两点，与x，y轴分别交于点C，D，试证明： $A C = B D$ ．
小华：如图2，直线 $y = 3 x - 4$ 与双曲线 $y = \frac{6}{x}$ 联立可得 $3 x^{2} - 4 x - 6 = 0$ ，进而求得 $x_{A} + x_{B}$ 与 $x_{C} + x_{D}$ 的值，由 $x_{C} + x_{D} = x_{A} + x_{B}$ ，证得线段AB的中点与线段CD的中点重合即可．
请完整的写出上述推理过程．

(2)、【深入探究】直线 $y = k x + b (k > 0)$ 与双曲线 $y = \frac{a}{x} (a > 0)$ 交于A，B两点，与x，y轴分别交于点C，D，试问： $A C = B D$ 还成立吗？请说明理由．

(3)、【模型应用】如图3，直线 $y = x + b$ 与双曲线 $y = \frac{a}{x} (a > 0)$ 交于A，B两点，与x，y轴分别交于点C，D．连接OA，OB．若 $△ A O C$ 的面积为 $5, 2 C D = A B$ ，求 $a$ 的值．

查看解析
15、如图，在四边形ABCD中，对角线AC与BD交于点O，已知OA=OC，OB=OD，过点O作EF⊥BD，分别交AB、DC于点E，F，连接DE，BF，

(1)、求证：△BOE=△DOF；

(2)、求证：四边形DEBF是菱形；

(3)、设AD∥EF，AD+AB=12，BD=4 $\sqrt{3}$ ，求AF的长.

查看解析
16、“端午杨梅挂篮头，夏至杨梅满山头”.端午期间，某水果店以每千克60元的价格出售杨梅，每天可卖出150千克，后期因杨梅的大量上市，水果店决定采用降价促销的方式吸引顾客，若已知杨梅售价每千克下降1元，则每天能多售出3千克（同一天中售价不变），

(1)、设售价每千克下降x元，则每天能售出千克（用含x的代数式表示）；

(2)、当杨梅每千克售价为多少元时，每天能获得9072元的销售额；

(3)、水果店定了“每天售出杨梅的销售额为10000元”的“小目标”，按题目的条件能否达成这个“小目标”？若能达成，求出达成时的售价：若不能达成，请说明理由。

查看解析
17、如图，在4x4的网格中（每个小正方形的边长为1），每个小正方形的顶点叫作格点，已知点A在格点上，仅用无刻度的直尺，按以下要求画四边形，使其各顶点都在格点上.

(1)、在图1中画一个以A为顶点，面积为6的平行四边形；

(2)、在图2中画一个以A为顶点，不是正方形的菱形；

(3)、在图3中画一个以A为顶点，面积最大的正方形，

查看解析
18、学校为加强学生垃圾分类方面的知识普及，开设了垃圾分类臻善德育小课培训学习，为了解培训效果，学校对七年级544名学生在学习前和培训后各进行一次垃圾分类知晓情况检测，两次检测项目相同，政教处依据同一标准进行问卷评估，分成“合格”、“良好”、“优秀”3个等级，依次记为2分、6分、8分，学校随机抽取32名学生的2次检测等级作为样本，绘制成如图的条形统计图：

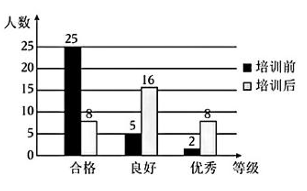(1)、这32名学生在培训前得分的中位数对应等级应为；（填“合格”、“良好”或“优秀”）

(2)、求这32名学生培训后比培训前的平均分提高了多少？

(3)、利用样本估计该校七年级学生中，培训后检测等级为“良好”与“优秀”的学生人数之和是多少?

查看解析
19、解方程：

(1)、2x²-x-6=0

(2)、（x-2）²=9x²

查看解析
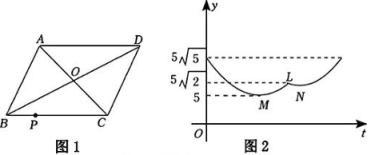
20、如图1，平行四边形ABCD中两条对角线AC、BD交于点O，AB=5 $\sqrt{5}$ ，点P从顶点B出发，沿B→C→D以每秒1cm的速度匀速运动到点D，图2是点P运动过程中线段OP的长度y与时间t的函数关系图象，其中M、N分别是两段曲线的最低点，则点M的横坐标为，点N的纵坐标为.

查看解析

上一页 1044 1045 1046 1047 1048 下一页跳转

x的取值	-2	2	a	0
分式的值	无意义	0	1	b

∠BAP	10°	20°	40°
∠G	80°	70°	▲
∠GAF	20°	40°	▲