-
1、如图，在正方形ABCD的对角线AC上取点E，F是AB上一点（不与点A、B重合）连结DE，EF，BE，若DE=EF，则∠DEF的大小为.
-
2、如图，▱ABCD的对角线AC，BD相交于点O，∠ADC的平分线与边AB相交于点P，E是PD的中点，若AD=4，CD=6，则EO的长为.
-
3、某药品原价每盒144元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒81元，则该药品平均每次降价的百分率是.
-
4、我国古代园林连廊常采用八角形的窗户设计，如图1所示，其轮廓是一个正八边形（边相等，内角相等），从窗户向外观看，景色宛如镶嵌于一个画框之中.图2是八角形窗户的示意图，它的一个外角∠1的大小为°.
-
5、如图，AC是正方形ABCD的对角线，点E是CD上一点，连结BE，分别过点A和C作BE的垂线，垂足分别为G和F，BE与AC交于点H，O是AC的中点，连结OF，OG，AB=5，有下列结论：①当AG=4时，FG=1；②OG平分∠AGE.关于这两个结论，下列说法正确的是（ ）
A、①②都对 B、①对，②错 C、①错，②对 D、①②都错 -
6、如图，两张宽度均为3cm的纸条交叉叠放在一起，交叉形成的锐角为60°，则重合部分构成的四边形ABCD的周长为（ ）
A、12cm B、6cm C、8cm D、4cm -
7、如图，E为▱ABCD的对角线AC上一点，AC=6，CE=1，连结DE并延长至点F，使得EF=DE，过点F作FM∥CD交AC于点M，连结BF，则BF的长为（ ）
A、 B、4 C、 D、5 -
8、已知关于x的方程kx2+（1-k）x-1=0，下列说法中正确的是（ ）A、当k=1时，方程有两个不相等的实根 B、当k=0时，方程无解 C、当k=-2时，方程只有一个实根 D、当k≠0时，方程一定有两个不相等的实根
-
9、如图为汽车常备的一种千斤顶的原理图，其基本形状是一个菱形ABCD，中间通过螺杆连结，转动手柄可改变∠BCD的大小（菱形的边长不变）.当∠BCA=26°时，则∠ADC的度数为（ ）
A、26° B、52° C、128° D、154° -
10、用反证法证明“在△ABC中，若∠A>∠B>∠C，则∠A>60°”时，应先假设（ ）A、∠A>60° B、∠A<60° C、∠A≠60° D、∠A≤60°
-
11、如图，已知△ABD，用尺规进行如下操作：①以点B为圆心，AD长为半径作弧；②以点D为圆心，AB长为半径作弧；③两弧在BD上方交于点C，连结BC，DC.可直接判定四边形ABCD为平行四边形的依据是（ ）
A、两组对边分别平行 B、一组对边平行且相等 C、两组对边分别相等 D、对角线互相平分 -
12、如图是上海今年春节七天最高气温（℃）的统计结果，这七天最高气温的众数和中位数是（ ）
A、15，17 B、17，17 C、17，14 D、17，15 -
13、要使在实数范围内有意义，则x的取值范围是（ ）A、x≤2 B、x>1 C、x≥0 D、x≥2
-
14、如图：
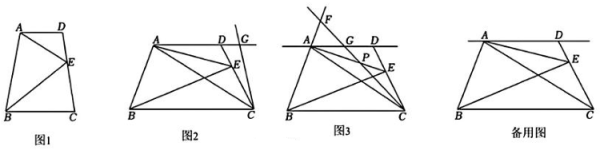(1)、【尝试应用】如图1，在四边形ABCD中，AD//BC，点E是线段CD上一点.∠AEB=70°，∠DAE=30°，求∠CBE的度数；(2)、【拓展提高】如图2，在四边形ABCD中，AD//BC，点E是线段CD上一点.若AE平分∠DAC，∠CAB=∠ABC.①试求出∠BAE的度数；
②已知∠AEB=∠ABE，∠EBC=30°，点G是直线AD上的一个动点，连接CG并延长.
Ⅰ.若CA恰好平分∠BCD，当CG与四边形ABCD中一边所在直线垂直时，∠ACG= ▲ .
Ⅱ.如图3，若CG是∠ACD的平分线与BA的延长线交于点F，与AE交于点P，且∠BFC=α°，则∠ADC= ▲ （用含α的代数式表示）.
-
15、根据以下信息，探索解决问题：
背景：为了提高产品的附加值，某公司计划将研发生产的1500件新产品进行加工后再投放市场，每天满工作量情况下，甲、乙两个工厂加工数量及每件加工费用保持稳定不变，公司派出相关人员分别到这两间工厂了解情况，获得如下信息，
信息1
每天满工作量情况下，乙工厂每天加工数量是甲工厂每天加工数量的1.5倍；
信息2
每天满工作量情况下，甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息3
每天满工作量情况下，甲工厂加工1天，乙工厂加工2天共需要10000元：甲工厂加工2天，乙工厂加工3天共需要16100元.
问题解决
问题1
设每天满工作量情况下，甲工厂每天加工数量为x件，结合信息1可得：乙工厂每天加工数量为 ▲ 件（请用x的代数式表示）.
问题2
每天满工作量情况下，求甲工厂每天能加工多少件新产品？
问题3
公司将1500件新产品交给甲、乙两工厂一起加工，发现这批新产品的平均加工费用为整数，两工厂加工的时间之和不是整数，请问交给甲工厂多少件新产品进行加工？
-
16、用若干块如图所示的正方形或长方形纸片拼成图（1）和图（2）.
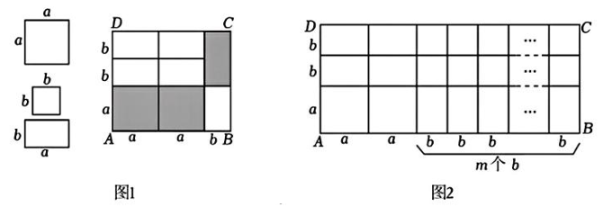(1)、如图1，若长方形ABCD的面积为56，其中阴影部分的面积为26，a>b，求a-b的值.(2)、如图2，若AD的长度为6，AB的长度为n.①当m= ， n=时，a，b的值有无数组；
②当m ， n时，a，b的值不存在.
-
17、如图，已知AB//CD，AD平分∠EAC，∠B=∠D.
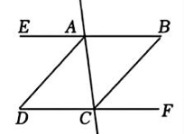(1)、请说明AD//BC：(2)、若∠DAC=（2x+15）°，∠B=（105-3x）°，求∠D的度数. -
18、如图，在10×8的正方形网格中，每个小正方形的边长为1，其顶点称为格点，格点△ABC与点D的位置如图所示.
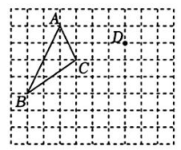(1)、平移格点△ABC，画出平移后的格点△DEF（点A，B，C的对应点分别为点D，E，F）；(2)、连接AD，CF，则线段AD与线段CF的关系是.(3)、四边形ADFC的面积为. -
19、计算下列各题：(1)、；(2)、
-
20、用面积都为1的长方形纸片①、②围成长方形ABCD，如图所示，其中四边形MNPQ也是长方形.设AE=x，DE=y，且x>y·
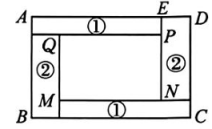(1)、AB=.(2)、若x2-3xy+y2=0，则=.