相关试卷

1、如图，将周长为10的 $△ A B C$ 沿BC方向平移2个单位得到 $△ D E F$ ，则四边形ABFD的周长为。

查看解析
2、若分式 $\frac{3}{m - 2}$ 有意义，则实数 $m$ 的取值范围是．

查看解析
3、如图，已知AB//CD，P为CD下方一点，G，H分别为AB，CD上的点，∠PGB=α，∠PHD=β，（α>β，且a，β均为锐角），∠PGB与∠PHD的角平分线交于点F，GE平分∠PGA，交直线HF于点E，下列结论：
①∠P=a-β：②2∠E+α=180°+β：③若∠CHP-∠AGP=∠E，则∠E=60°；
其中正确的序号是（）

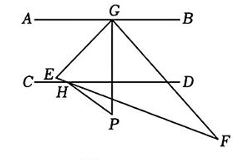A、①② B、②③ C、①③ D、①②③

查看解析
4、已知 $a > 1$ ， $P = \frac{a}{a - 1}$ ， $Q = \frac{a - 1}{a}$ ， $R = \frac{a}{a + 1}$ ，则P、Q、R的大小关系是（）

A、 $R > P > Q$ B、 $P > Q > R$ C、 $P > R > Q$ D、 $R > Q > P$

查看解析
5、《九章算术》“盈不足”一卷中有这样一个问题：“今有善田一亩，价三百：恶田七亩，价五百，今并买一百亩，价钱一万，问善、恶田各几何？”意思是：“今有好田1亩，价值300钱；坏田7亩，价值500钱.今共买好、坏田100亩，总价值10000钱，问好、坏田各买了多少亩？设好田买了x亩，坏田买了y亩，则下面所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 100 \\ 300 x + \frac{7}{500} y = 10000 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ 300 x + \frac{500}{7} y = 10000 \end{array}$ C、 ${\begin{array}{l} x + y = 100 \\ \frac{7}{500} x + 300 y = 10000 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ \frac{500}{7} x + 300 y = 10000 \end{array}$

查看解析
6、已知 $3^{a} \div 3^{b} = 9$ ， $a^{2} + b^{2} = 6$ ，则ab的值为（）

A、-2 B、-1 C、1 D、2

查看解析
7、已知关于x，y的方程组 ${\begin{array}{l} 4 x + y = 12 \\ 3 x - 2 y = a \end{array}$ 的解为 ${\begin{array}{l} x = b \\ y = 4 \end{array}$ ，则a的值为（）

A、-2 B、0 C、2 D、4

查看解析
8、下列各式中能用完全平方公式进行因式分解的是（）

A、 $x^{2} + x + 1$ B、 $x^{2} + 2 x - 1$ C、 $x^{2} - 1$ D、 $x^{2} + 6 x + 9$

查看解析
9、如图.已知直线a//b，将一块含30°角的直角三角板ABC按如图方式放置（∠ACB=30）其中点A，B分别落在直线a、b上.若∠1=44°，则∠2的度数为（）

A、45° B、46° C、47° D、22°

查看解析
10、下列计算正确的是（）

A、 $x^{2} \cdot x^{2} = 2 x^{2}$ B、 $(x y)^{3} = x y^{3}$ C、 $(x^{4})^{2} = x^{8}$ D、 $x^{2} + x^{2} = x^{4}$

查看解析
11、冠状病毒的一个变种是非典型肺炎的病原体，球形冠状病毒的直径是0.00000012米，则这种冠状病毒的直径用科学记数法表示为（）

A、 $1.2 \times 1 0^{- 7}$ 米 B、 $1.2 \times 1 0^{- 8}$ 米 C、 $12 \times 1 0^{- 8}$ 米 D、 $12 \times 1 0^{- 7}$ 米

查看解析
12、定义：若分式A与分式B的差等于它们的积.即 $A - B = A B$ ，则称分式B是分式A的“可存异分式”。如 $\frac{1}{x + 1}$ 与 $\frac{1}{x + 2}$ ：因为 $\frac{1}{x + 1} - \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ， $\frac{1}{x + 1} \times \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ，所以 $\frac{1}{x + 2}$ 是 $\frac{1}{x + 1}$ 的“可存异分式”。

(1)、填空：分式 $\frac{1}{x + 2}$ （填“是”或“不是”）分式 $\frac{1}{x + 3}$ 的“可存异分式”。

(2)、已知分式 $\frac{2 x + 3}{3 x + 3}$ 是分式A的“可存异分式”。
①求分式A的表达式；
②若整数x使得分式A的值是正整数，直接写出分式A的值。

(3)、若关于x的分式 $\frac{n + 2}{m x + m^{2} + n}$ 是关于x的分式 $\frac{m - 1}{m x + n^{2}}$ 的“可存异分式”，求 $m + n$ 的值。

查看解析
13、若x=1+ a^p ， y=1+ a-^p ，其中a是不为0的常数，p是正整数。

(1)、用含x的代数式表示y。

(2)、若x＝a，x⋅ y=1，求p的值。

查看解析
14、如图，A，B，C，D四点在同一直线上，BE交CF于点O，∠1＝∠2，∠BED＝∠F，则DE∥CF。请完成下面的说理过程。
解：已知∠1＝∠2，
根据（   ），
得    ▲        ∥    ▲        。
又根据（   ），得▲    ▲    ＝∠BOC。
又因为∠BED＝∠F，
所以    ▲    ＝    ▲    。
根据（    ），所以    ▲    ∥    ▲    。

查看解析
15、对于有理数x和y，定义新运算：x⊙y＝ax＋by，其中a、b是常数，已知2⊙4＝12，4⊙10＝2．

(1)、求a、b的值；

(2)、若x＝1，x⊙y＝6，求y的值．

查看解析
16、如图，在6×6的网格中，点A，B，C均在格点上，分别按下列要求作出经平移所得的图形。

(1)、把△ABC向右平移3格。

(2)、把第（1）题中平移所得的图形再向上平移2格。

查看解析
17、因式分解：

(1)、 $m^{2} - 9$ 。

(2)、 $4 a^{3} - 12 a^{2} + 9 a$ 。

查看解析
18、

(1)、计算： $(- 1)^{2} + 2^{- 2} - (π - 3)^{0}$ 。

(2)、化简： $(a + 2)^{2} + (2 + a) (3 - a) - 10$ 。

查看解析
19、如图，直线 $A B / / C D$ ，点E，F在AB上，点M，N在CD上，已知EM平分 $∠ N E F, M F$ 平分 $∠ D M E$ ， $E N ⊥ F N$ ，记 $∠ M F N, ∠ C N E$ 的度数分别为 $α, β$ ，则 $\frac{α}{β}$ 的值为。

查看解析
20、若 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是方程组 ${\begin{array}{l} a x - b y = 9 \\ b x - a y = 4 \end{array}$ 的解，则 $a^{2} - b^{2}$ 的值是.

查看解析

上一页 1040 1041 1042 1043 1044 下一页跳转