相关试卷

1、 $s i n 45 ° =$

查看解析
2、已知关于x的二次函数 $y = x^{2} - (k + 1) x + \frac{1}{4} k^{2}$ 的图象与x轴有两个交点，则 $\sqrt{{(1 + k)}^{2}}$ 化简后的结果为（）

A、 $1 + k$ B、 $1 - k$ C、 $- k - 1$ D、 $k - 1$

查看解析
3、如图， $P A$ 与 $⊙ O$ 相切于点 $A$ ， $P B$ 与 $⊙ O$ 相切于点 $B$ ， $M$ 为 $\overset{⌢}{A B}$ 上一点，过点 $M$ 与 $⊙ O$ 相切的直线分别交 $P A$ ， $P B$ 于点 $E$ ， $F$ ．若 $△ P E F$ 的周长为 $10$ ，则 $P A$ 的长为（）

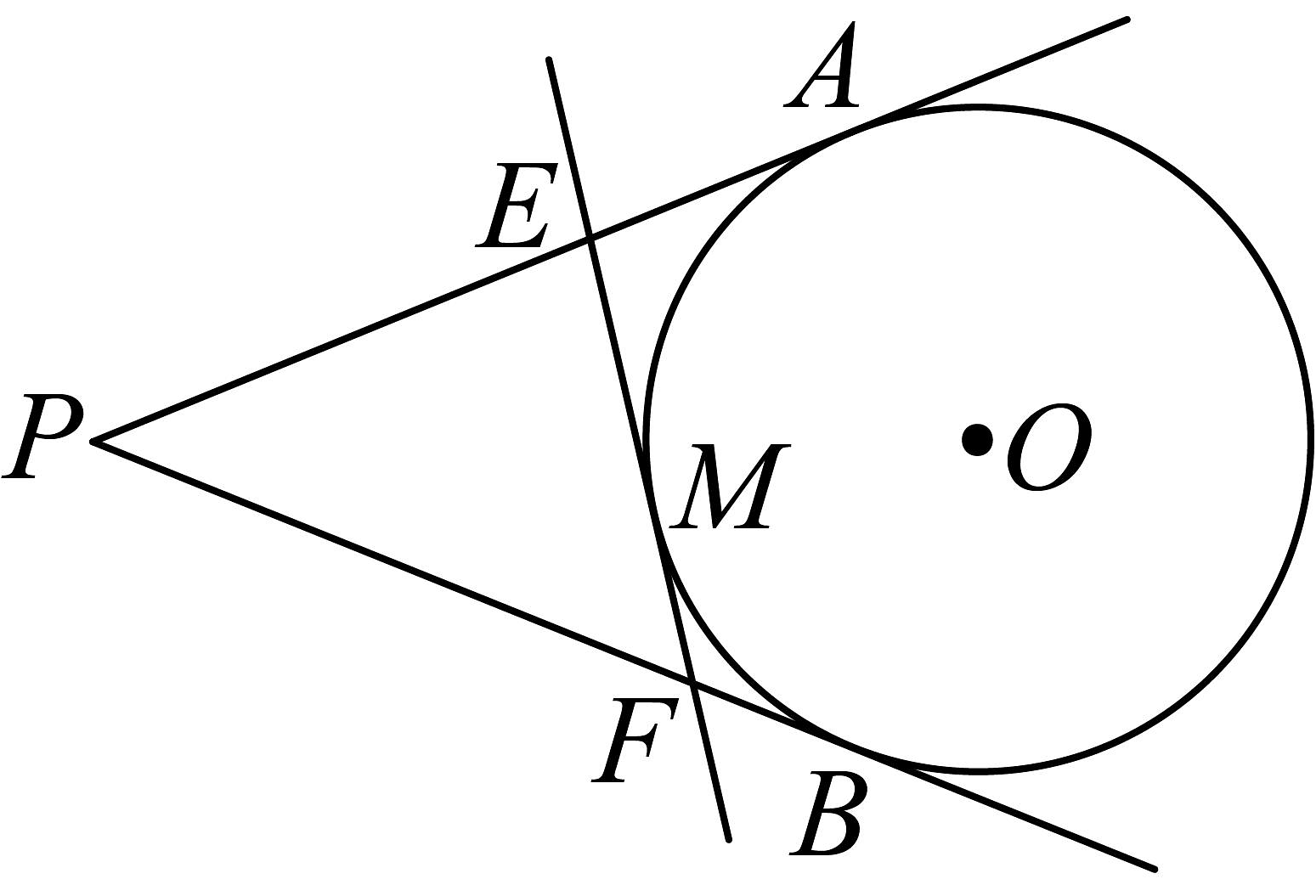A、3 B、4 C、5 D、10

查看解析
4、如图，在 $△ A B C$ 中， D， E分别是 $A B ， B C$ 的中点．若 $△ B D E$ 的面积是1，则 $△ A C D$ 的面积是（）

A、1 B、2 C、3 D、4

查看解析
5、从 $- 2$ ， $- 1$ ， 3中任意取一个数作为正比例函数 $y = k x$ 中的k，则正比例函数 $y = k x$ 的图象经过第一、第三象限的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看解析
6、下列因式分解正确的是（）

A、 $2 m - n = 2 (m - n)$ B、 $m^{2} + n^{2} = {(m + n)}^{2}$ C、 $m^{2} + m = m (m - 1)$ D、 $m^{2} - 4 = (m + 2) (m - 2)$

查看解析
7、一个三角形的两边长分别为2和3，则第三边的长可以是（）

A、1 B、2 C、6 D、9

查看解析
8、下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $2 a^{2} + a = a^{3}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $3 a^{4} \div a = 3 a^{4}$

查看解析
9、小 $D N A$ 病毒是一类已知最小的动物 $D N A$ 病毒，已知某种小 $D N A$ 病毒的直径约为 $23nm$ ，即 $0.000000023 m$ ．数据“ $0.000000023$ ” 用科学记数法可表示为（）

A、 $2.3 \times 10^{- 8}$ B、 $2.3 \times 10^{- 9}$ C、 $0.23 \times 10^{- 7}$ D、 $23 \times 10^{- 9}$

查看解析
10、AI是人工智能的英文缩写，下列4个AI品牌的图标是中心对称图形的是（）

A、 B、 C、 D、

查看解析
11、2025的相反数为（）

A、 $- \frac{1}{2025}$ B、 $\frac{1}{2025}$ C、 $- 2025$ D、2025

查看解析
12、如图，已知AD//BC，∠A=∠C=m°.

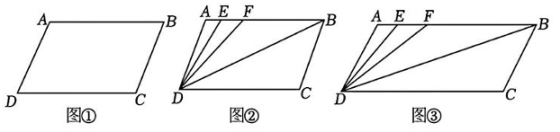(1)、如图①，求证：AB//CD；

(2)、如图②，连结BD，若点E，F在线段AB上，且满足∠FDB=∠BDC，并且DE平分∠ADF，求∠EDB的度数；（用含m的代数式表示）

查看解析
13、某杨梅园的杨梅除了直接销售到市区外，还可以让市民去园区采摘，已知杨梅在市区和园区的销售价格分别是15元/千克和10元/千克，该杨梅园今年六月第一周一共销售了1000千克，销售收入12000元.

(1)、该杨梅园今年六月第一周市区和园区分别销售了多少千克杨梅？

(2)、为了促销，该杨梅园决定六月第二周将市区和园区销售价格均以相同折扣进行销售，小方发现用3240元购买市区的重量比用2430元购买园区的重量少30千克，求本次活动对市区和园区进行几折销售？

(3)、在（2）的促销条件下，杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等，若第二周杨梅在市区的销量为a千克，园区的销量为b千克，请直接写出а与b的数量关系.

查看解析
14、如图，点D，E分别在AABC的边AB，AC上，点F在线段CD上，且∠3=∠B，EFllAB.

(1)、求证：DE//BC；

(2)、若DE平分∠ADC，∠2=4∠B，求∠1.

查看解析
15、已知实数x，y满足：x+y=7，xy=12．

(1)、求x²+y²的值；

(2)、将长方形ABCD和长方形CEFG按照如图方式放置，其中B，C，G三点在同一条直线上，点E在x边CD上，连接BD，BF，已知AD=x，AB=nx，FG=y，EF=ny，阴影部分的面积为14，求n的值.

查看解析
16、先化简，再求值： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后再从1，2，3中选一个合适的数，求式子的值.

查看解析
17、解下列方程（组）：

(1)、 ${\begin{array}{l} 5 x + 4 y = - 15 \\ 5 x - 3 y = 6 \end{array}$ ；

(2)、 $\frac{2}{x - 2} - \frac{4 x}{x^{2} - 4} = 0$ .

查看解析
18、因式分解：

(1)、 $4 m x - 6 m y + 2 m$ ；

(2)、 $4 x^{2} y + 4 x y^{2} + y^{3}$ .

查看解析
19、如图所示，数学拓展课上，小聪将直角三角形纸片 $A B C (∠ A = 2 5^{°}, ∠ B = 6 5^{°})$ 沿DE向下折叠，点 $A$ 落在点 $A^{^{'}}$ 处，当 $E A^{^{'}} / / B C$ 时， $∠ 1 =$ 度．

查看解析
20、已知关于 $x$ 的分式方程 $\frac{2}{1 - x} = \frac{m x}{x - 1} - 2$ 有增根，则 $m$ 的值是．

查看解析

上一页 1039 1040 1041 1042 1043 下一页跳转