-
1、如果规定汽车向东行驶3千米记作千米,那么向西行驶5千米记作( )千米A、 B、 C、 D、3
-
2、已知,抛物线(),与x轴交于A,B,(点A在点B的左侧)与y轴交于点C,顶点为点D.
 (1)、抛物线的对称轴为 (用含有a的式子表示);(2)、若当时,函数值y随着x的增大而减小,求a的取值范围;(3)、如图1,当时,点为第四象限的抛物线上一点,过点E作轴与抛物线另外一个交点为点F.
(1)、抛物线的对称轴为 (用含有a的式子表示);(2)、若当时,函数值y随着x的增大而减小,求a的取值范围;(3)、如图1,当时,点为第四象限的抛物线上一点,过点E作轴与抛物线另外一个交点为点F.①连接 , 过点E作轴,交于点H,以为邻边构造矩形 , 当矩形的周长为时,求m的值;
②以所在直线为对称轴将抛物线位于下方的部分翻折,若翻折后所得部分与x轴有交点,且交点都位于x轴正半轴,请直接写出n的取值范围.
-
3、【问题初探】
(1)如图1,动点A在半径为2的上,若 , 直接写出的最小值.
由于和都是定长,当点A,B,O形成三角形时,霖霖想到了“三角形两边之差小于第三边”,由此可知当点A在上时对应的就是最小的情形.按照霖霖的思路,请直接写出最小值.
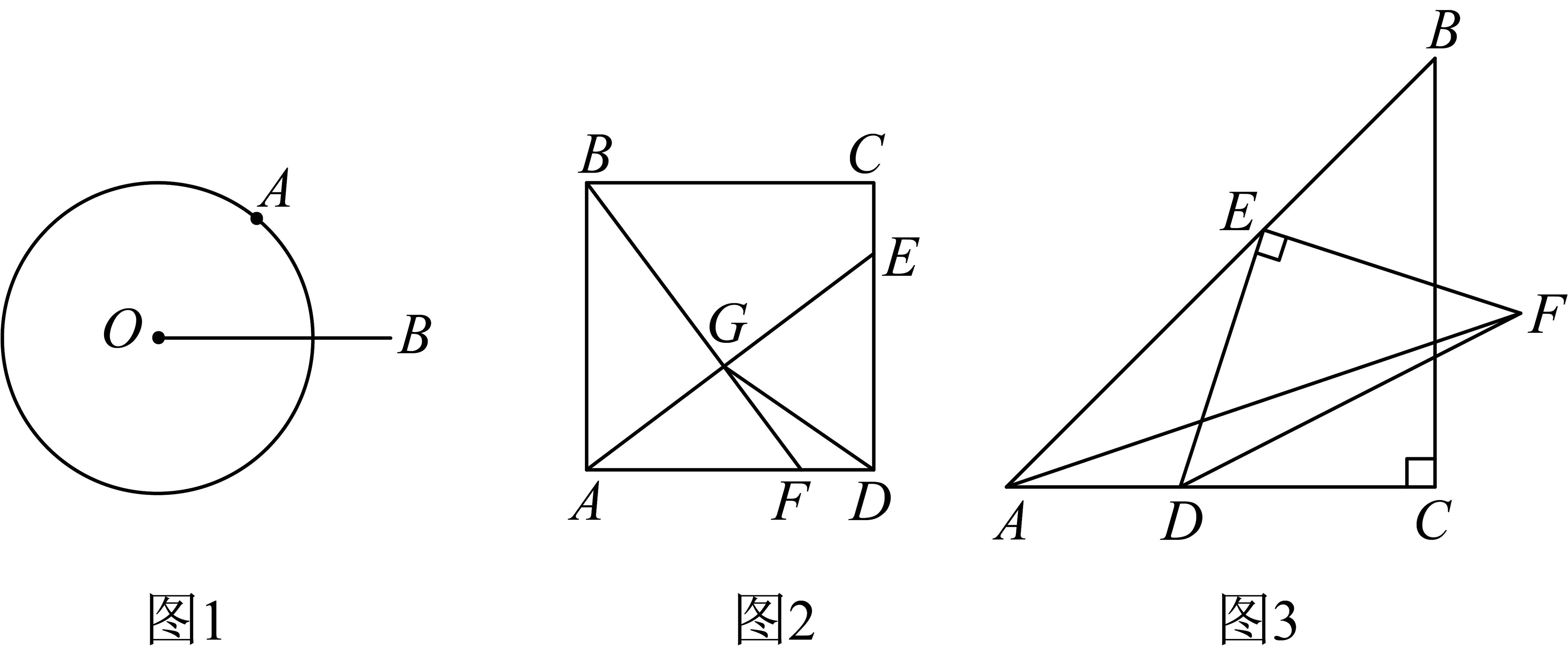
【类比分析】
(2)如图2,点E和F分别是边长为4的正方形边和上的两个动点,且 , 连接和交于点G,连接 , 求的最小值.
霖霖尝试着绘制了点E在不同位置的几张图,目测始终都是直角,于是联想到了“圆周角所对的弦是直径”,也就是说“点G是正方形内以为直径的圆弧上的点”,进而本题可以类比图1获解,清按照霖霖的思路完成求最小值的解题过程.以下是证明的部分过程
证明:

∴可判断点G的轨迹,即的最小值为_________.
请补全缺失的证明过程.
【学以致用】
(3)如图3,是两块等腰直角三角板, , , . 当点D和E同时在边和上滑动时,点F也随之移动,若连接 , 则的最大值是_________.
-
4、图1是煤油温度计,该温度计的左侧是华氏温度(),右侧是摄氏温度().华氏温度与摄氏温度之间存在着某种函数关系,小明通过查阅资料和观察温度计,得到了如表所示的数据.
摄氏温度值
0
10
20
30
40
华氏温度值
32
50
68
86
104
 (1)、在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;(2)、求y与x之间的函数解析式;(3)、某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16.求该温度区间的最大温差是多少摄氏度.
(1)、在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;(2)、求y与x之间的函数解析式;(3)、某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16.求该温度区间的最大温差是多少摄氏度. -
5、一项知识问答竞赛要求以团队方式参赛,每个团队20名选手.某校准备参加此项竞赛,前期组建了两个团队,经过一段时间的培训后,对两个团队进行了一次预赛,对成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.
a.一队成绩的频数分布直方图如下(数据分成4组:):

b.二队成绩如下:
68 69 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.一、二两队成绩的平均数、众数、中位数如下:
平均数
众数
中位数
一队
79.6
77
P
二队
79.25
m
q
根据以上信息,回答下列问题:
(1)、m的值为___________,p___________q(填“”“”或“”);(2)、若两队都各去掉一个最高分和一个最低分,则下列判断正确的是___________;A.一队成绩的方差增大,二队成绩的方差减小 B.两队成绩的方差都增大
C.一队成绩的方差减小,二队成绩的方差增大 D.两队成绩的方差都减小
(3)、为了选出冲击个人冠军的种子选手,学校对这次成绩90分以上的甲、乙、丙三位同学又单独进行了5次测试,平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前.这5次测试的成绩如下:测试1
测试2
测试3
测试4
测试5
甲
90
94
90
94
91
乙
91
92
92
92
93
丙
93
90
92
93
k
若丙的排序居中,则表中k(k为整数)的值为___________.
-
6、用一元一次不等式(组)解应用题.
某次数学竞赛中出了10道题,每答对1题得5分,每答错1题或不答扣3分,问至少要答对几道题,得分不低于10分.
-
7、一次访谈活动,主办方邀请9名学生参加活动,在场地安排了9把椅子(每个方格代表一把椅子,横为排,竖为列)按图示方式摆放,其中圆点表示已经有学生入座的椅子如果有五名学生入座(剩余座位分别记为A,B,C,D),又有甲、乙两名同学随机入座,请用树状图或列表法求甲和乙坐在同一横排且相邻的概率.

-
8、已知 , 求代数式的值.
-
9、如图,正方形边长为2,在正方形内部,以为直径作半圆,点E是中点, , 分别与半圆交于点G,点F,连接 .

①;②;③;④;⑤点G、F是半圆的三等分点.
以上说法正确的有 . (只需填写序号即可)
-
10、如图,这是儿童玩具底板的一幅图案,供小朋友拼图用的是正方形的木块和正n边形木块.由于小朋友只选了正方形的木块,导致没有拼成.老师鼓励他选取正n边形的木块试试,他试了几次终于成功了.这里的 .

-
11、明代《算法统宗》有一首饮酒诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多薄酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今25位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.可列方程组为 .
-
12、如图,在数轴上表示实数的点可能是 .

-
13、由火柴棒摆成的3个图案如图所示,按图中规律摆放,则第n个图案需要根火柴棒.

-
14、分解因式: .
-
15、已知 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、
-
16、如图,将三角形纸片按下面四种方式折叠,则是的高的是( )A、
 B、
B、 C、
C、 D、
D、
-
17、从电动伸缩门可以抽象出如图所示几何图形,若平分 , 交于点 . 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、实数a,b在数轴上的对应点的位置如图所示,下列结论中错误的是( )
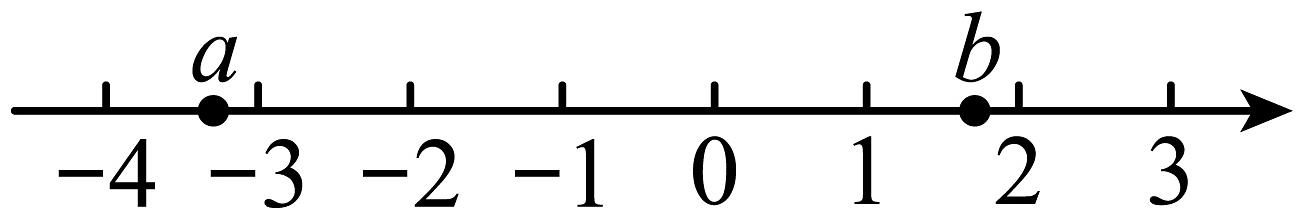 A、 B、 C、 D、
A、 B、 C、 D、 -
19、在平面直角坐标系中,若两个二次函数的表达式的系数符合特征:①二次项系数互为相反数,②一次项系数相等,③常数项互为相反数,我们称这两个二次函数互为“旋转抛物线”.例如:抛物线与互为“旋转抛物线”.
 (1)、抛物线的“旋转抛物线”的表达式为_____;(2)、如图 , 若()中的抛物线与的顶点分别为点 , 它们的交点分别为 . 分别连接 , , , , 试判断四边形的形状,并说明理由;(3)、在()的条件下,如图 , 连接 . 若为抛物线位于第四象限的图象上一动点,作直线 , 与抛物线交于另一点 , 与抛物线依次交于点(点位于第二象限).若 , 求的值.
(1)、抛物线的“旋转抛物线”的表达式为_____;(2)、如图 , 若()中的抛物线与的顶点分别为点 , 它们的交点分别为 . 分别连接 , , , , 试判断四边形的形状,并说明理由;(3)、在()的条件下,如图 , 连接 . 若为抛物线位于第四象限的图象上一动点,作直线 , 与抛物线交于另一点 , 与抛物线依次交于点(点位于第二象限).若 , 求的值. -
20、如图1,将一副直角三角板放在同一条直线上,其中 , , .
 (1)、观察猜想:将图1中的三角尺绕逆时针的方向旋转至如图2的位置,使得 , 交于点 , 则的度数为_____;(2)、操作探究:如图2所示,在(1)的条件下,已知 , , 求此时线段的长度;(3)、深化拓展:将图1中的三角尺绕点逆时针的方向旋转至如图3的位置(),线段与交于点 , 点在线段上,求的值.
(1)、观察猜想:将图1中的三角尺绕逆时针的方向旋转至如图2的位置,使得 , 交于点 , 则的度数为_____;(2)、操作探究:如图2所示,在(1)的条件下,已知 , , 求此时线段的长度;(3)、深化拓展:将图1中的三角尺绕点逆时针的方向旋转至如图3的位置(),线段与交于点 , 点在线段上,求的值.