-
1、下列运算正确的是( )A、 B、 C、 D、
-
2、2024年,我国申报的“春节——中国人庆祝传统新年的社会实践”非遗项目,列入联合国教科文组织的人类非物质文化遗产代表作名录.春节民间钧有剪窗花的习俗,人们用剪窗花来表达自己庆贺新春的欢乐心情.下面是某同学为首个非遗蛇年春节设计的四种窗花,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
3、下列实数中,最小的是( )A、2025 B、2024 C、 D、
-
4、如图,在中, , , D、E为上两点, , F为外一点,且 , , 则以下结论:①;②;③;④ . 其中正确的是( )
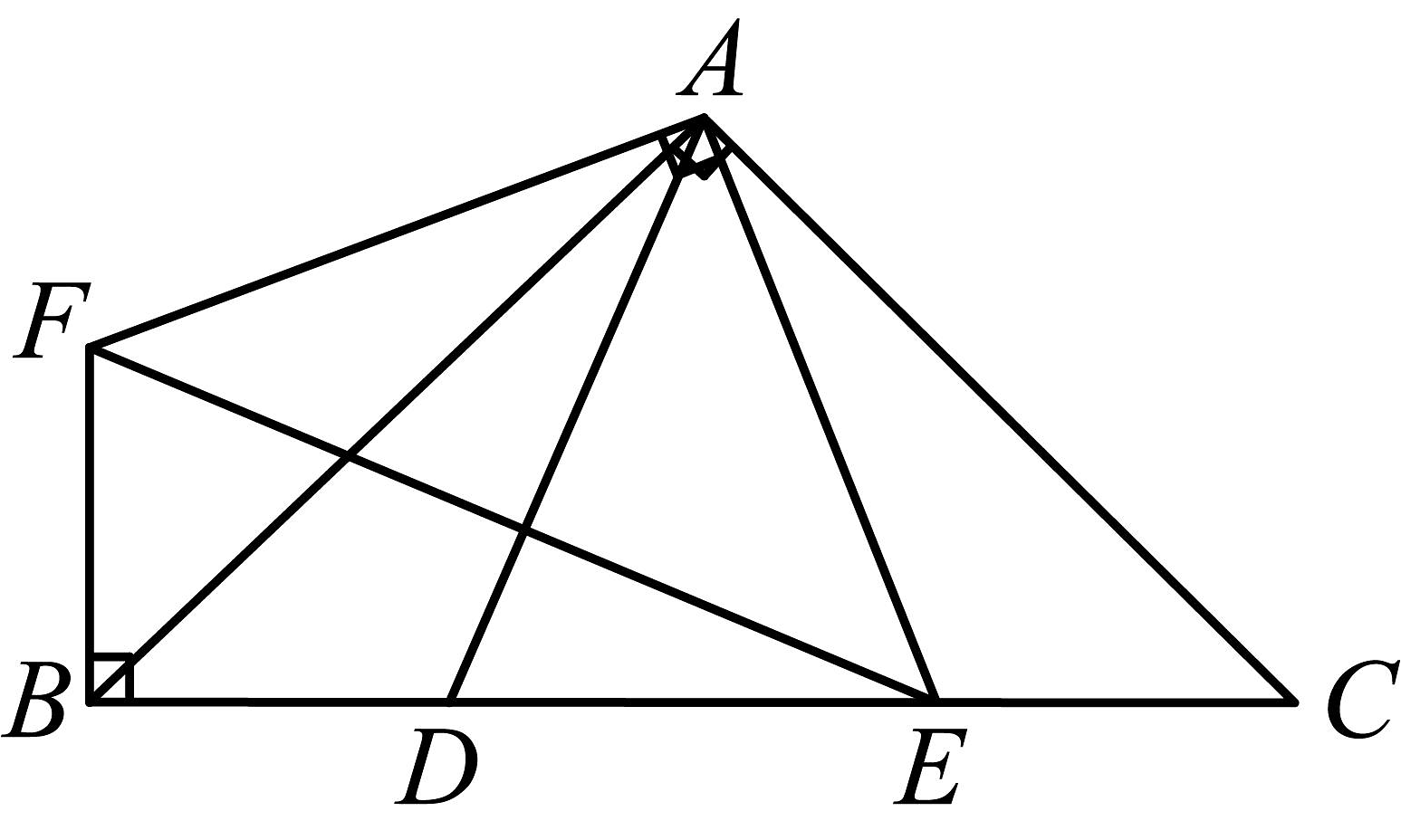 A、①②③④ B、②③④ C、①③④ D、②④
A、①②③④ B、②③④ C、①③④ D、②④ -
5、如图1,古代叫“斗”,官仓、粮栈、米行、家里等都是必备的粮食度量用具.图2是它的几何示意图,下列说法正确的是( )
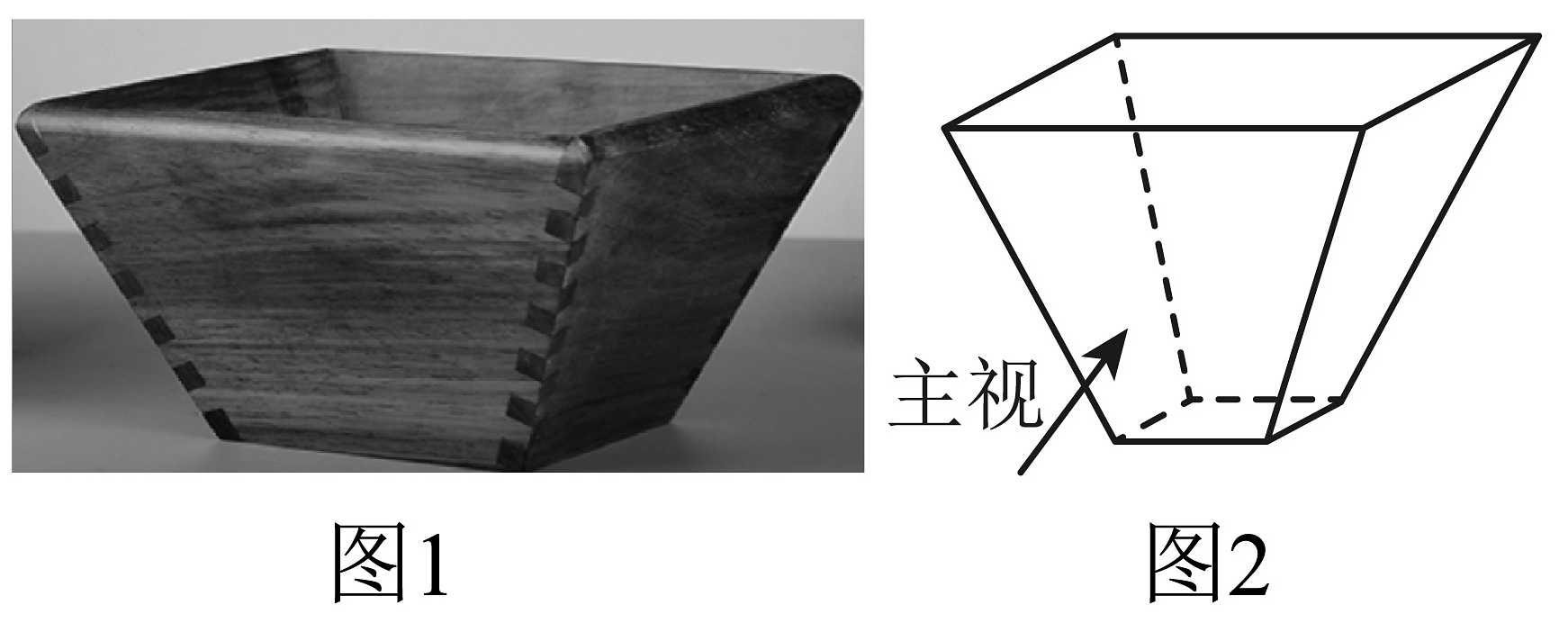 A、主视图和左视图相同 B、主视图和俯视图相同 C、左视图和俯视图相同 D、三个视图都相同
A、主视图和左视图相同 B、主视图和俯视图相同 C、左视图和俯视图相同 D、三个视图都相同 -
6、如图,正六边形内接于 , , 则的长为( )
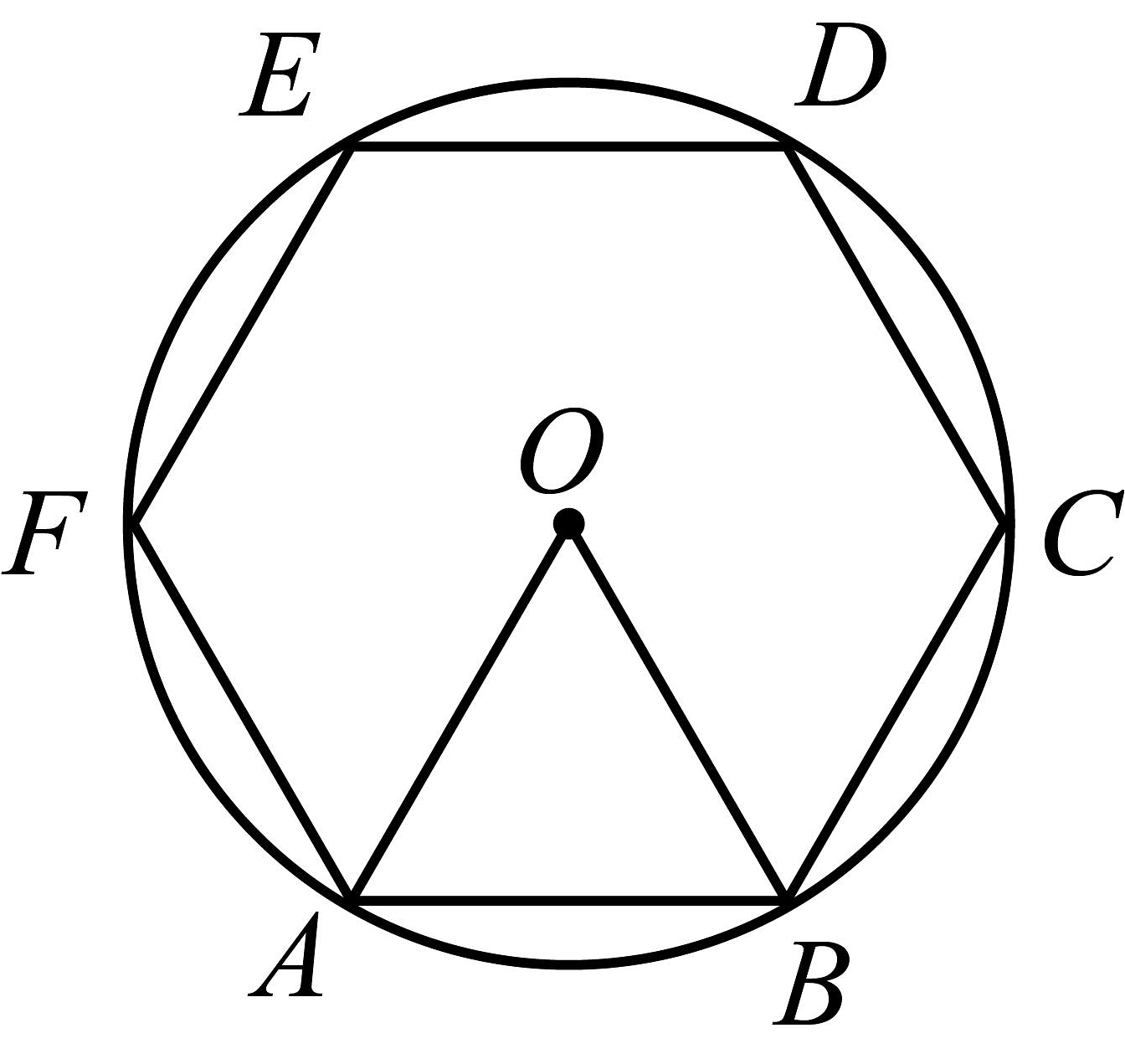 A、2 B、 C、1 D、
A、2 B、 C、1 D、 -
7、如图,抛物线过点 , 顶点为Q,抛物线(其中t为常数,且),顶点为P.
 (1)、求出a的值和点Q的坐标;(2)、佳佳说:无论t取何值,将的顶点Q向左平移2个单位长度后一定落在上;
(1)、求出a的值和点Q的坐标;(2)、佳佳说:无论t取何值,将的顶点Q向左平移2个单位长度后一定落在上;琪琪说:无论t为何值,总经过一个定点;
请选择一人的说法进行说理;
(3)、当时,①求直线的解析式;
②作直线 , 当l与的交点到x轴的距离恰为6时,求l与x轴交点的坐标.
-
8、在中, , 点是边上一点(点不与端点重合).点关于直线的对称点为点 , 连接 . 在直线上取一点 , 使 , 直线与直线交于点 .
 (1)、如图1,若 , 求的度数(用含的代数式表示);(2)、如图1,若 , 用等式表示线段与之间的数量关系,并证明;(3)、如图2,若 , 点从点移动到点的过程中,连接 , 当为等腰三角形时,请直接写出此时的值.
(1)、如图1,若 , 求的度数(用含的代数式表示);(2)、如图1,若 , 用等式表示线段与之间的数量关系,并证明;(3)、如图2,若 , 点从点移动到点的过程中,连接 , 当为等腰三角形时,请直接写出此时的值. -
9、如图1,是正方形对角线上一点,以为圆心,长为半径的与相切于点 , 与相交于点 .
 (1)、求证:与相切.(2)、若正方形的边长为 , 求的半径.(3)、如图2,在(2)的条件下,若点是半径上的一个动点,过点作交于点 . 当时,求的长.
(1)、求证:与相切.(2)、若正方形的边长为 , 求的半径.(3)、如图2,在(2)的条件下,若点是半径上的一个动点,过点作交于点 . 当时,求的长. -
10、如图,在平面直角坐标系内,一次函数与反比例函数交于、两点.
 (1)、求反比例函数的解析式;(2)、若一次函数与x轴、y轴分别交于A、B两点,过的顶点能不能画出直线把分成面积相等的两部分?若能,请求出这样的直线所对应的函数表达式.
(1)、求反比例函数的解析式;(2)、若一次函数与x轴、y轴分别交于A、B两点,过的顶点能不能画出直线把分成面积相等的两部分?若能,请求出这样的直线所对应的函数表达式. -
11、周末,小明的父母带着他和妹妹一起去湿地公园放风筝.如图1,妹妹的身高为1.50米,风筝线长(近似的看作直线)与水平地面构成角,米.如图2,小明的身高米,风筝线长(近似的看作直线)米.
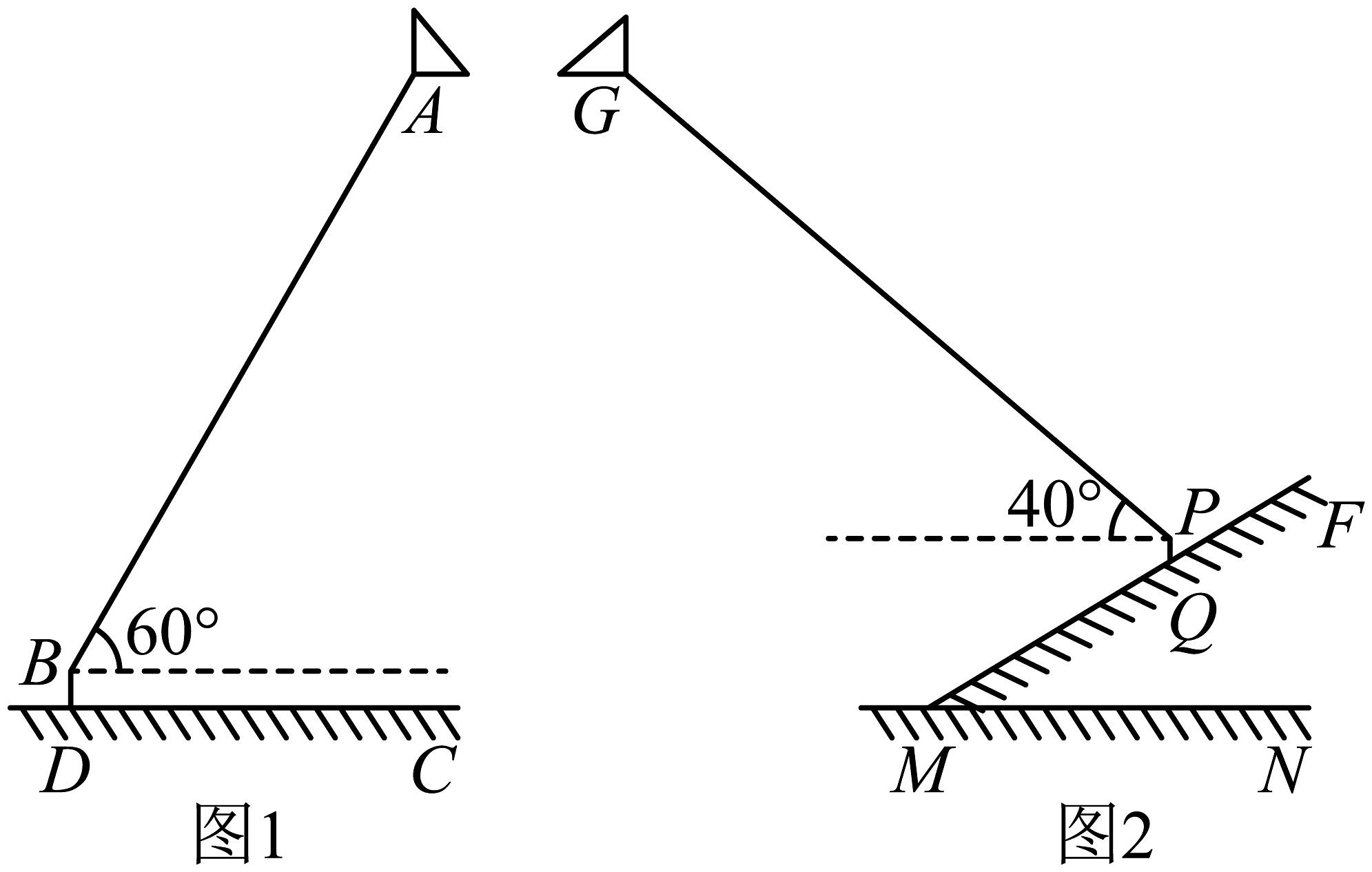 (1)、求妹妹的风筝离水平地面的高度(结果保留两位小数);(2)、小明勇于挑战,把放风筝的位置选在一个坡度的斜坡上,且坡长米,风筝线与水平面构成角.请问小明和妹妹谁放的风筝离水平地面高?(参考数据,)
(1)、求妹妹的风筝离水平地面的高度(结果保留两位小数);(2)、小明勇于挑战,把放风筝的位置选在一个坡度的斜坡上,且坡长米,风筝线与水平面构成角.请问小明和妹妹谁放的风筝离水平地面高?(参考数据,) -
12、为做好青少年禁毒教育宣传工作,某校开展了主题为“珍爱生命,拒绝毒品”的知识竞赛(共20题,每题5分,满分100分).该校从学生成绩都不低于80分的九年级(1)和(3)班中,各随机抽取了20名学生成绩进行整理,绘制了不完整的统计表、条形统计图及分析表.
【收集数据】
九年级(1)班20名学生成绩:85,95,100,90,90,80,85,90,80,100,80,85,95,90,95,95,95,95,100,95.
九年级(3)班20名学生成绩:90,80,100,95,90,85,85,100,85,95,85,90,90,95,90,90,95,90,95,95.
【描述数据】九年级(1)班20名学生成绩统计表
分数
80
85
90
95
100
人数
3
3
a
7
3
九年级(3)班20名学生成绩条形统计图

【分析数据】九年级(1)班和(3)班20名学生成绩统计表
统计量/班级
平均数
中位数
众数
方差
九年级(1)班
m
n
95
41.5
九年级(3)班
91
90
p
26.5
【应用数据】根据以上信息,回答下列问题:
(1)、请补全条形统计图;(2)、填空:________,________,________;(3)、你认为哪个班级的成绩更好一些?请说明理由;(4)、从上面5名的100分的学生中,随机抽取2名学生参加市级知识竞赛,请用列表法或画树状图法求所抽取的2名学生恰好在同一个班级的概率. -
13、如图,在中,延长到E点,使 , 连结 , 与交于点O,连结、 .
 (1)、求证:;(2)、求证: .
(1)、求证:;(2)、求证: . -
14、解不等式组: , 并在数轴上表示其解集.

-
15、计算: .
-
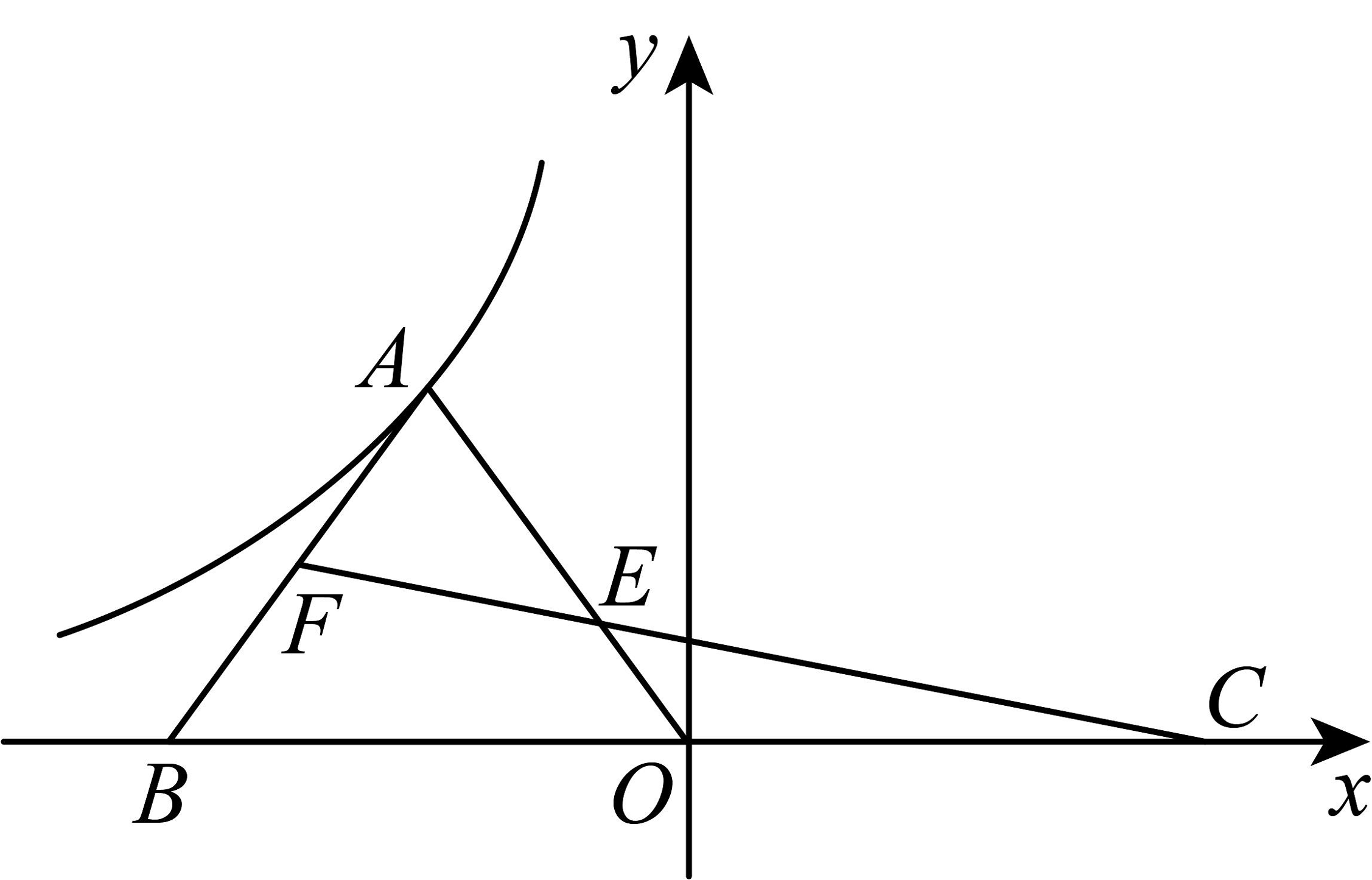
16、如图,等边的顶点A在双曲线且底边在x轴上,F为中点,O为的中点,连接交于E,四边形的面积为4,则 .
-
17、如图,点是矩形中边上的一点,沿折叠为 , 点落在上.若的大小为 , 且满足 , 则的值为 .

-
18、如图,过圆外一点向圆O做两条切线分别是和 , 已知圆的半径为3, , 求弦 .

-
19、如图,小明同学按如下步骤作四边形:①画2个单位长度的线段;②以点A、C为圆心,2个单位长为半径画弧,分别于点B,D;③连接 , 则的大小是 .

-
20、分式有意义,则的取值范围是 .