-
1、等分圆是指将一个圆周均匀分割成多个相同长度的弧段,每个弧段对应的圆心角相等.小南学习了等分圆后,尝试着编了一道题:如图,已知的半径长为2,点 , , , , , 将六等分,连接 , , , , 发现恰好过圆心 , 过点作的垂线,交的延长线于点 , 连接 .
 (1)、°;(2)、在(1)的结论下,求的长;(3)、求图中阴影部分的面积.
(1)、°;(2)、在(1)的结论下,求的长;(3)、求图中阴影部分的面积. -
2、某学习小组成员对无人机烟花(如图①)的绽放高度非常感兴趣,开展了“测量无人机烟花绽放高度”的实践活动.如图②,已知一无人机烟花在A点绽放,测角仪在处测得无人机烟花绽放点A的仰角为 , 在处测得无人机烟花绽放点A的仰角为 . 点 , 在同一水平地面上,线段 , 钓与地面垂直, , .
(参考数据: , , . )
 (1)、过点A作于点 , 连接交于点 , 若 , 则(用含的代数式表示).(2)、在(1)的条件下,求无人机烟花绽放点离地面的高度.
(1)、过点A作于点 , 连接交于点 , 若 , 则(用含的代数式表示).(2)、在(1)的条件下,求无人机烟花绽放点离地面的高度. -
3、每年的4月23日是“世界读书日”,某校为了让学生学会读书,爱上读书,准备购进一批心理学书籍和科技类书籍放在学校和班级的图书馆及图书角里,其中购买3本心理学书籍和4本科技类书籍共需240元,购买6本心理学书籍和5本科技类书籍共需390元.(1)、求心理学书籍和科技类书籍的单价各是多少元?(2)、若该校想要购进心理学书籍和科技类书籍共80本,要求心理学书籍不低于50本,设购买心理学书籍本,付款金额为元,请求出与的表达式,并求当为多少本时,有最小值,最小值是多少元?
-
4、如图,在四边形中, , 点 , 点分别在边 , 上,连接 , , 若 , .
 (1)、求证:四边形是矩形;(2)、若 , , 求的面积.
(1)、求证:四边形是矩形;(2)、若 , , 求的面积. -
5、某市中考改革后,将地理、生物两个科目纳入等级考试,等级分为 , , , 四个等级.规定:这两科考试成绩均达到等级及以上可以报考省级示范性高中:两科考试成绩均达到等级及以上可以报考一般普通高中.某校为了解本届八年级学生地理、生物的成绩情况,组织了这两科目的模拟考试,并从八年级学生中随机抽取了名学生的两科考试成绩制作了如下的统计图.根据这些信息,解答下列问题:
 (1)、被抽取的名学生中,某学生的生物模拟考试成绩为分,则该生的地理模拟考试成绩为分;(2)、根据历届成绩分析,地理成绩达分及以上能评定为等级及以上,生物成绩达分及以上能评定为等级及以上.该校本届八年级共有学生人,请估计该校能报考省级示范性高中的学生人数;(3)、小沐同学在本次模拟考试中两科成绩均高于分,爸爸想奖励带她去看两场电影,但是目前只有四部电影上映(依次记为 , , , ),于是爸爸将四张完全相同的卡片分别写上 , , , , 背面朝上洗匀放好,要求小沐从中随机抽取两张卡片.请用列表或画树状图的方法,求小沐抽到的两张卡片恰好是和的概率.
(1)、被抽取的名学生中,某学生的生物模拟考试成绩为分,则该生的地理模拟考试成绩为分;(2)、根据历届成绩分析,地理成绩达分及以上能评定为等级及以上,生物成绩达分及以上能评定为等级及以上.该校本届八年级共有学生人,请估计该校能报考省级示范性高中的学生人数;(3)、小沐同学在本次模拟考试中两科成绩均高于分,爸爸想奖励带她去看两场电影,但是目前只有四部电影上映(依次记为 , , , ),于是爸爸将四张完全相同的卡片分别写上 , , , , 背面朝上洗匀放好,要求小沐从中随机抽取两张卡片.请用列表或画树状图的方法,求小沐抽到的两张卡片恰好是和的概率. -
6、如果用眼不科学,坐姿不正确,就容易导致视力下降.经调查发现,近视眼镜的度数(度)与镜片的焦距(米)是反比例函数关系,图象如图所示:
 (1)、写出这一函数表达式;(2)、小妮原来佩戴200度的近视眼镜,由于用眼不科学,导致视力下降,经复查验光后,所配镜片的焦距调整到了0.25米,求小妮现在的眼镜度数比原来的眼镜度数增加了多少度?
(1)、写出这一函数表达式;(2)、小妮原来佩戴200度的近视眼镜,由于用眼不科学,导致视力下降,经复查验光后,所配镜片的焦距调整到了0.25米,求小妮现在的眼镜度数比原来的眼镜度数增加了多少度? -
7、(1)请从以下个式子中,任选个式子进行减法运算:
, , , , ,
(2)解分式方程: .
-
8、如图,在矩形中,点为边的中点,点在边上,连接 , , 两线段交于点 , 过点作交于点 , 若 , , , 则的长为 .

-
9、如图,已知直线与直线交于点 , 则关于的不等式的解集为 .

-
10、如图,在平行四边形中,对角线 , 交于点 , 过点作的垂线交于点 , 连接 . 已知的周长是 , 则平行四边形的周长是 .

-
11、化简的结果是 .
-
12、二次函数的图象如图所示,对称轴为直线 , 若关于的一元二次方程(为实数)在的范围内有解,则的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、小妍同学在翻阅《九章算术》时,看到这样一个问题:“今有二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”题目大意为:甲、乙两人各有钱若干,若乙将他所有钱的给甲,则甲有钱50;若甲将他所有钱的给乙,则乙也有钱50,问甲、乙原本各有多少钱?
为解决这个问题,小妍设甲原有钱,乙原有钱,可以得到方程组( )
A、 B、 C、 D、 -
14、开窗通风是日常生活中保持室内空气流通的一种方法,图是平开窗的打开实物图,图是平开窗打开的效果图,此时,窗户打开了 , 窗户底边长是 , 则这扇窗户底边端点扫过区域的轨迹长(弧长)是( )
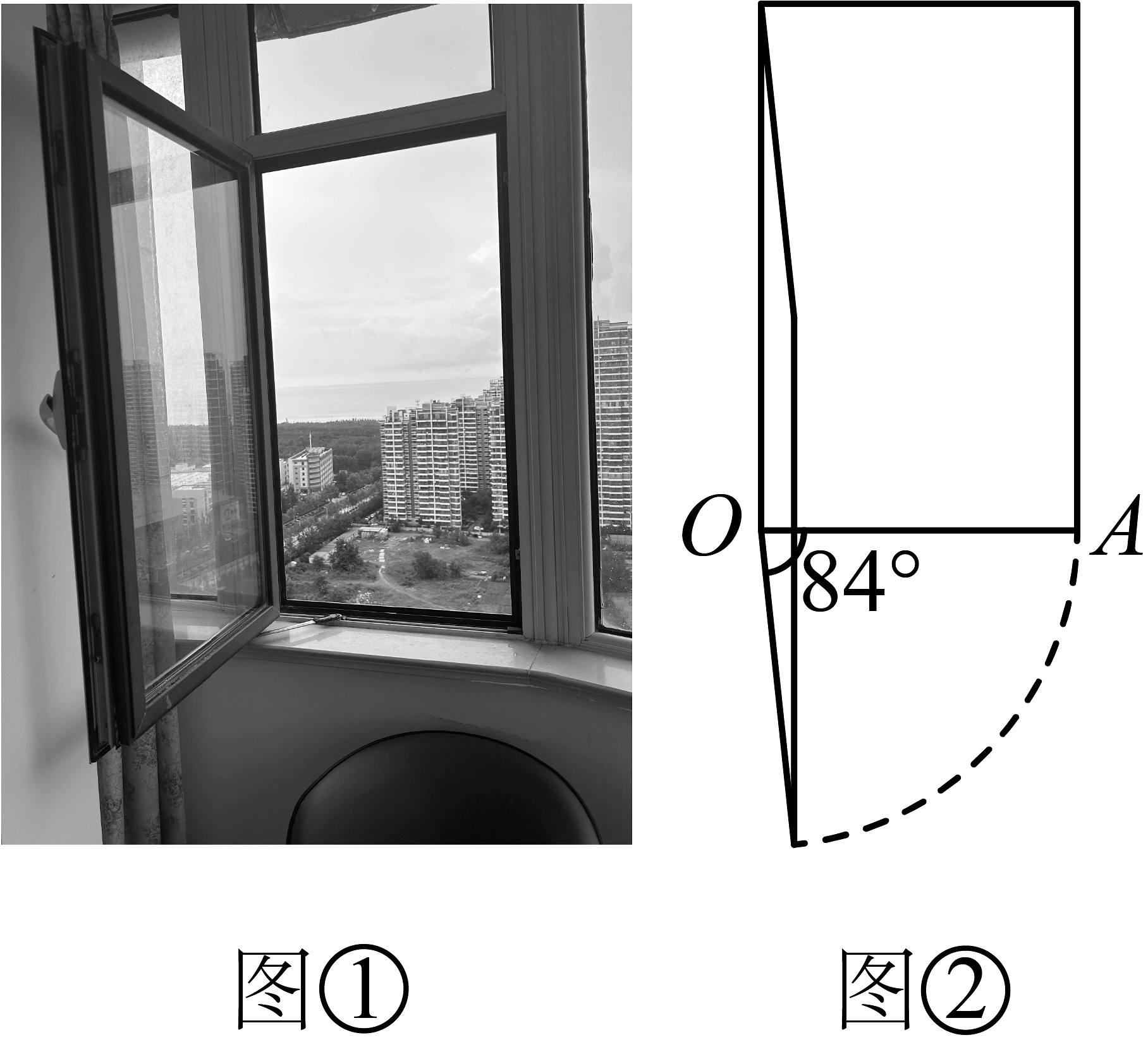 A、 B、 C、 D、
A、 B、 C、 D、 -
15、在学习“用频率估计概率”这节课时,教材“读一读”环节介绍了“估计6个人中有2个人生肖相同的概率”的模拟试验,课后某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人生肖相同的概率”,他们将试验中获得的数据记录如下:
试验次数
100
200
500
1000
2000
3000
“有2个人生肖相同”的次数
24
53
126
259
522
780
“有2个人生肖相同”的频率
0.24
0.265
0.252
0.259
0.261
0.26
通过试验,该小组估计“6个人中有2个人生肖相同”的概率(精确到0.01)大约是( )
A、 B、 C、 D、 -
16、小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.如图是小孔成像原理的示意图,长的蜡烛在暗盒中所成的像的长是 , 蜡烛到小孔的距离为 , 则像到小孔的距离为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、投壶是中国古代一种传统礼仪和宴饮游戏.某校2025年迎新活动中,九年级(1)班5名同学参加投壶游戏体验传统民俗,每人有10支箭进行投壶,投进去的箭数分别为:6,8,5,9,7(单位:支),某同学求得这组数据的平均数为7支,则这组数据的方差是( )A、2 B、3 C、4 D、5
-
18、多项式因式分解正确的是( )A、 B、 C、 D、
-
19、若一元二次方程的一个根是 , 则另一个根是( )A、4 B、1 C、0 D、
-
20、南南在画板上画出两条不平行的直线 , (如图①),他发现,如果利用平移变换就可以知道这两条直线所成的角的度数:将直线向左平移与直线交于一点(如图②),则直线 , 所成的锐角的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、