-
1、代数式有意义,则x的取值范围为 .
-
2、已知 , 则整数 .
-
3、一个点的纵坐标是横坐标的2倍,则称这个点为“二倍点”,在的范围内,若二次函数的图象上至少存在一个“二倍点”,则c的取值范围是( )A、 B、 C、 D、
-
4、在平面直角坐标系中,已知点 , , 以原点为位似中心,位似比为 , 把缩小,则点A的对应的坐标是( )A、 B、 C、或 D、或
-
5、下列运算中正确的是( )A、 B、 C、 D、
-
6、下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
7、在 , , , 四个数中,最大的数是( )A、 B、 C、0 D、
-
8、【模型建立】
(1)如图1,点E是正方形边上一点,连接 , 过点B作交于点F,交于点G,用等式写出线段、的数量关系,并说明理由;

【模型应用】
(2)如图2,点E是正方形边上一点,连接 , 过点E作交于点G,交延长线于点M,请探究线段、、之间的数量关系,并说明理由;
【模型迁移】
(3)如图3,当点E在的延长线上时,连接 , 过点E作交的延长线于点G,交延长线于点M,请直接写出线段、、之间的数量关系,并说明理由.
-
9、解不等式组 , 并把解集在数轴上表示出来.
-
10、计算:
-
11、对于非零的两个实数 , 定义一种新运算“&”,规定 , 例如 , 则的值为 .
-
12、如图,在矩形中,对角线相交于点O, , , 则的长 .

-
13、若m,n是一元二次方程的两个根,则 .
-
14、如图①.在菱形中, , M是对角线上一动点,过点M作的垂线分别交折线 , 于点E,F,若点M沿的方向匀速运动,运动到点C停止,设 , 扫过菱形内部的面积记为y,y与x的函数图象如图②所示,则的长为( )
 A、2 B、 C、3 D、
A、2 B、 C、3 D、 -
15、为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班50名同学进行了问卷调查(每名同学只选其中的一类),依据50份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图(如图所示).下列说法正确的是( )
 A、班主任采用的是抽样调查 B、喜爱动画节目的同学最多 C、喜爱戏曲节目的同学有6名 D、“体育”对应扇形的圆心角为
A、班主任采用的是抽样调查 B、喜爱动画节目的同学最多 C、喜爱戏曲节目的同学有6名 D、“体育”对应扇形的圆心角为 -
16、类比思维是根据两个具有相同或相似特征的事物间的对比,从某一事物的某些已知特征去推测另一事物的相应特征存在的思维活动.请尝试用类比思维解决以下问题:
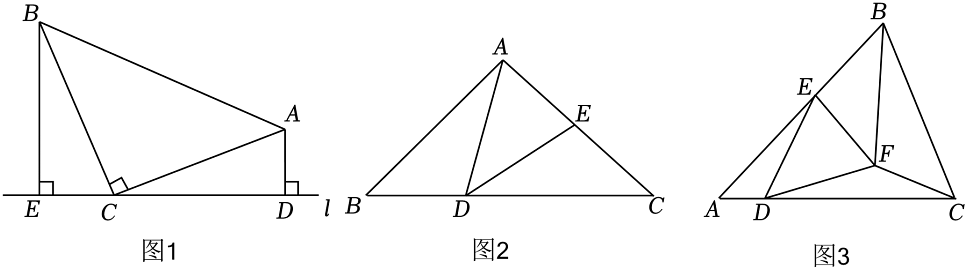 (1)、如图1,在等腰直角三角形中, , , 直线l经过点C,过点A作于点D,过点B作于点E,直接写出、、之间的数量关系: ;(2)、如图2,在中, , 点D、E分别在边、上,且 , . 若 , , 求的长度(用含a,b的代数式表示).(3)、如图3,在中, , , 点D、E分别是边、上的动点,以为腰向右作等腰 , 使得 , 且 , 连接、 , .
(1)、如图1,在等腰直角三角形中, , , 直线l经过点C,过点A作于点D,过点B作于点E,直接写出、、之间的数量关系: ;(2)、如图2,在中, , 点D、E分别在边、上,且 , . 若 , , 求的长度(用含a,b的代数式表示).(3)、如图3,在中, , , 点D、E分别是边、上的动点,以为腰向右作等腰 , 使得 , 且 , 连接、 , .①求证:;
②在点D、E运动过程中,点F位置也随之发生改变,若 , 当线段取得最小值时,求的面积.
-
17、【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形 . 把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为: , 图2中阴影部分面积可表示为 , 因为两个图中的阴影部分面积是相同的,所以可得到等式: .
【拓展探究】图3是一个长为 , 宽为的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.
(1)根据图形可得到一个关于、、的等量关系式是 ▲ ;
(2)结合以上信息,灵活运用公式,解决如下问题:
①已知 , , 则 ▲ .
②已知 , 求的值.
【知识迁移】
(3)如图5,红岭中学前不久举办了第一届“智启未来,科技筑梦”校园科技节活动,其中创意竞赛要求设计一款由两个正方形构成的光学元件模型.其中大正方形与小正方形的边长分别为a和b . 已知两正方形边长之和 , 边长之积 , 且E为中点.模型中阴影部分为特殊光线吸收区域,其面积大小直接影响光学元件对光线的吸收效果,进而决定模型的光学性能.为优化设计,需精确计算图中阴影部分的面积总和,求该阴影部分面积总和.

-
18、如图,平分 , 点P在上,于D, , 点E是射线上的动点,则的最小值为 .

-
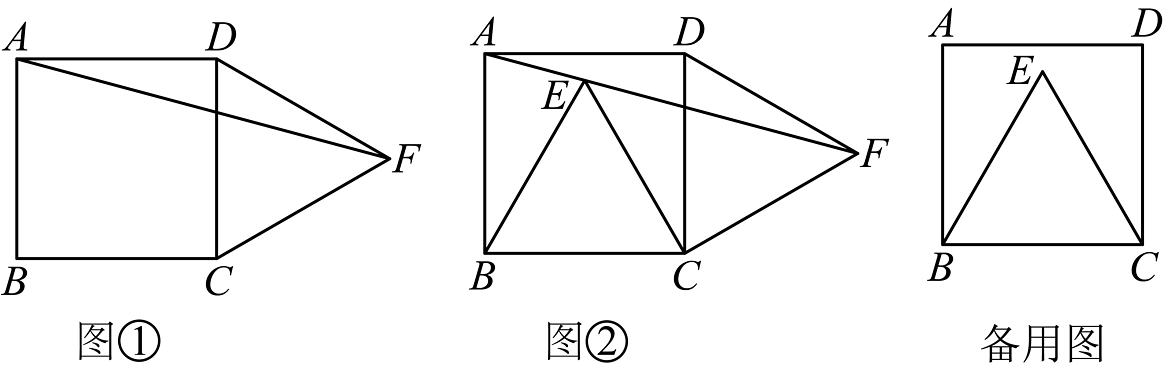
19、(1)【试题改编】小聪同学将教材习题进行了如下改编:如图①,四边形是正方形,是一个等边三角形,连接 , 则________;
(2)【深入探索】小悦同学接着小聪同学所编的题目继续进行改编:如图②,点在正方形内部,且是一个等边三角形,此时发现点恰好在上,提出问题:你能证明吗?
(3)【能力升华】老师看到小聪和小悦编的题后,非常高兴,稍作思考,也提出一个问题:在正方形中,点在正方形内部,且是一个等边三角形,以为边作等边三角形 , 连接 , , , 直接写出的值.
-
20、如图①,在平面直角坐标系中,二次函数的图象交轴于 , 两点,交轴于点 , 若点的坐标为 , 点是该二次函数图象上的一个动点,且在第一象限.
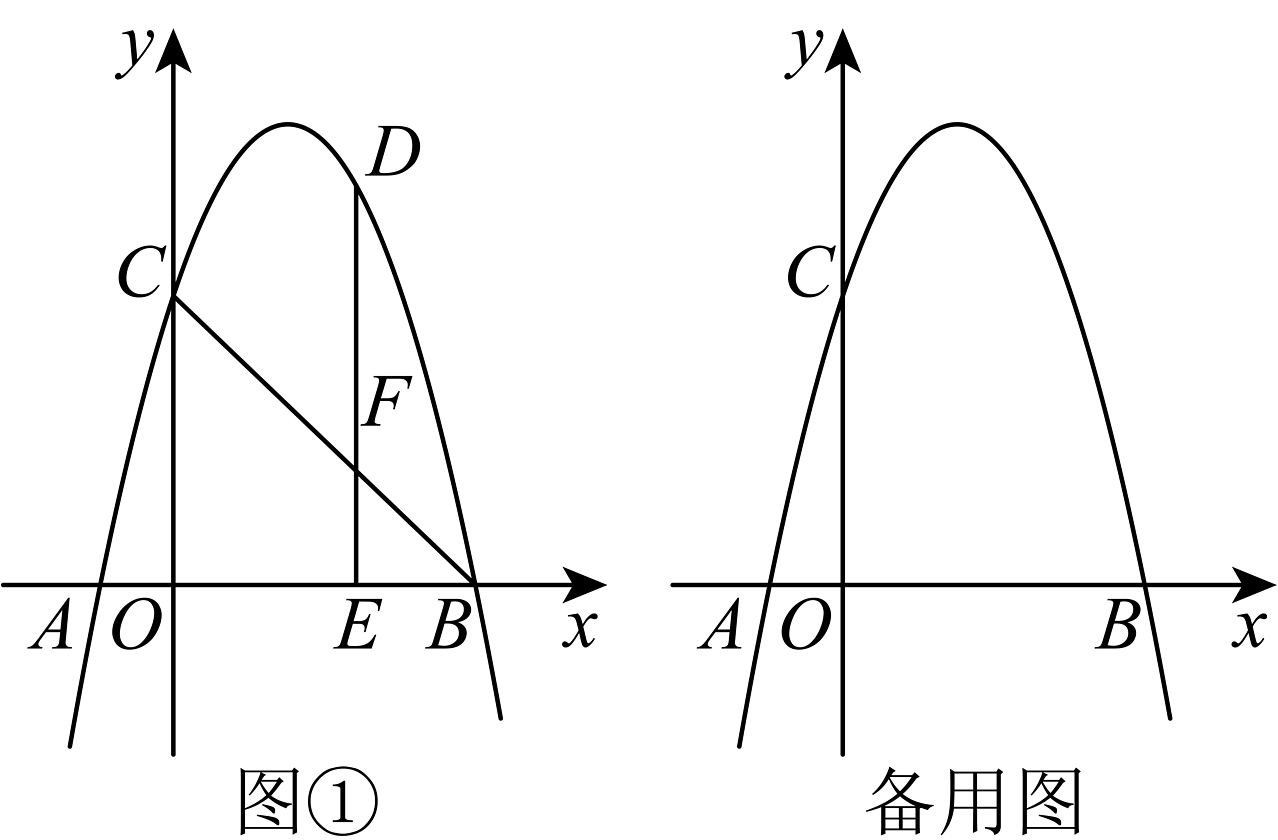 (1)、求二次函数的表达式;(2)、连接 , 过点作轴于点 , 交线段于点 , 当点运动到什么位置时,线段有最大值?请求出点的坐标和的最大值;(3)、连接 , , 若关于轴的对称图形是 , 是否存在点 , 使得四边形为菱形?若存在,求出点的坐标,若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、连接 , 过点作轴于点 , 交线段于点 , 当点运动到什么位置时,线段有最大值?请求出点的坐标和的最大值;(3)、连接 , , 若关于轴的对称图形是 , 是否存在点 , 使得四边形为菱形?若存在,求出点的坐标,若不存在,请说明理由.